External Language Model Integration for Factorized Neural Transducers

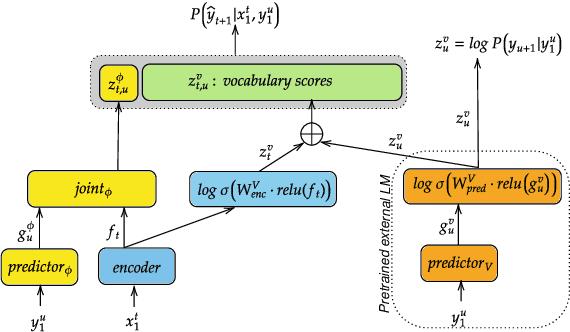
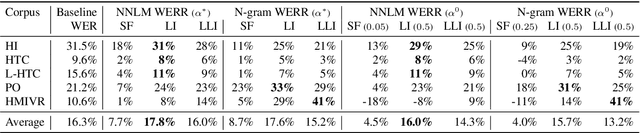
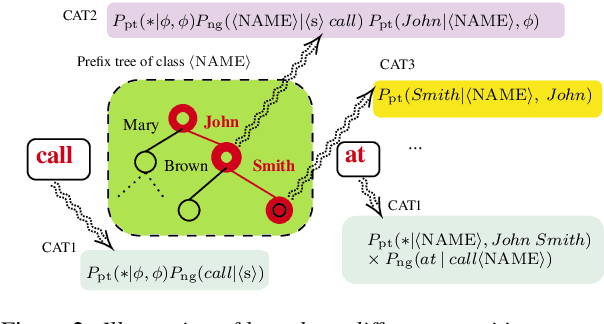
We propose an adaptation method for factorized neural transducers (FNT) with external language models. We demonstrate that both neural and n-gram external LMs add significantly more value when linearly interpolated with predictor output compared to shallow fusion, thus confirming that FNT forces the predictor to act like regular language models. Further, we propose a method to integrate class-based n-gram language models into FNT framework resulting in accuracy gains similar to a hybrid setup. We show average gains of 18% WERR with lexical adaptation across various scenarios and additive gains of up to 60% WERR in one entity-rich scenario through a combination of class-based n-gram and neural LMs.

Advances in Online Audio-Visual Meeting Transcription

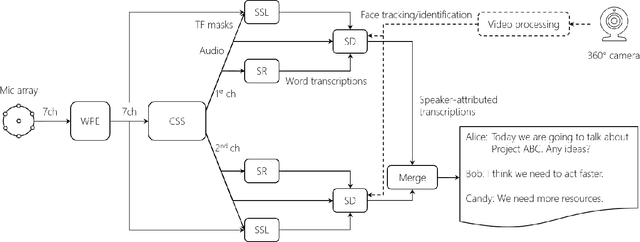
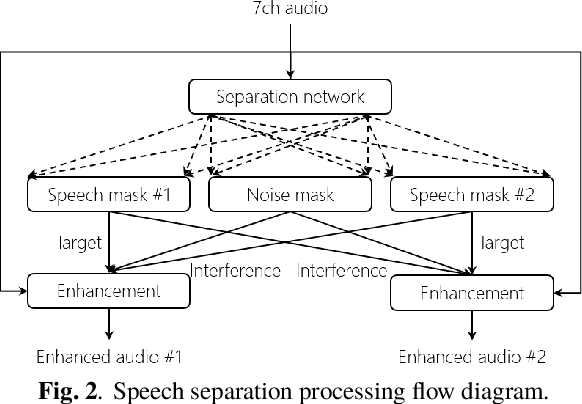
This paper describes a system that generates speaker-annotated transcripts of meetings by using a microphone array and a 360-degree camera. The hallmark of the system is its ability to handle overlapped speech, which has been an unsolved problem in realistic settings for over a decade. We show that this problem can be addressed by using a continuous speech separation approach. In addition, we describe an online audio-visual speaker diarization method that leverages face tracking and identification, sound source localization, speaker identification, and, if available, prior speaker information for robustness to various real world challenges. All components are integrated in a meeting transcription framework called SRD, which stands for "separate, recognize, and diarize". Experimental results using recordings of natural meetings involving up to 11 attendees are reported. The continuous speech separation improves a word error rate (WER) by 16.1% compared with a highly tuned beamformer. When a complete list of meeting attendees is available, the discrepancy between WER and speaker-attributed WER is only 1.0%, indicating accurate word-to-speaker association. This increases marginally to 1.6% when 50% of the attendees are unknown to the system.

Clustering and Community Detection with Imbalanced Clusters

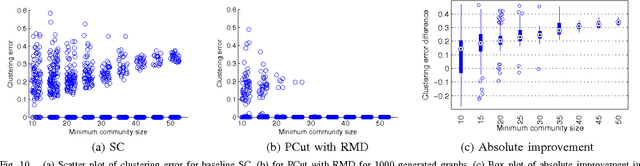
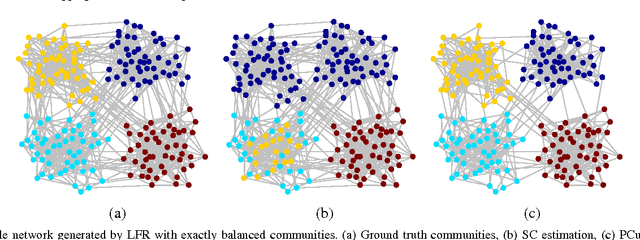
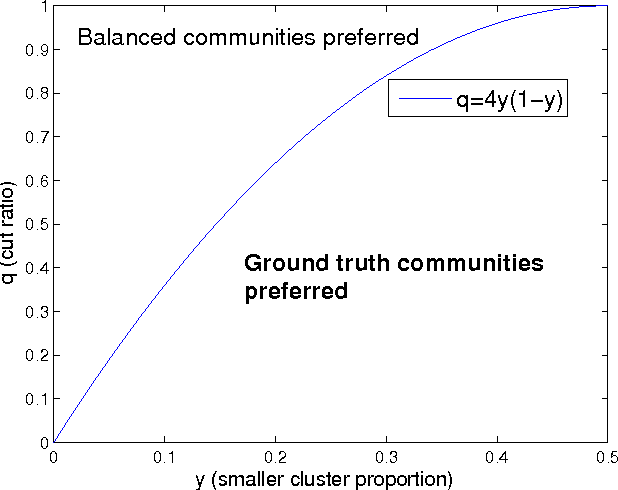
Spectral clustering methods which are frequently used in clustering and community detection applications are sensitive to the specific graph constructions particularly when imbalanced clusters are present. We show that ratio cut (RCut) or normalized cut (NCut) objectives are not tailored to imbalanced cluster sizes since they tend to emphasize cut sizes over cut values. We propose a graph partitioning problem that seeks minimum cut partitions under minimum size constraints on partitions to deal with imbalanced cluster sizes. Our approach parameterizes a family of graphs by adaptively modulating node degrees on a fixed node set, yielding a set of parameter dependent cuts reflecting varying levels of imbalance. The solution to our problem is then obtained by optimizing over these parameters. We present rigorous limit cut analysis results to justify our approach and demonstrate the superiority of our method through experiments on synthetic and real datasets for data clustering, semi-supervised learning and community detection.

Sparse Signal Processing with Linear and Nonlinear Observations: A Unified Shannon-Theoretic Approach

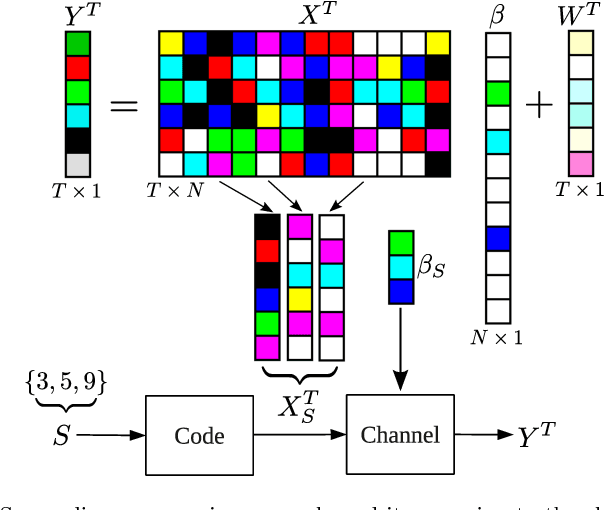
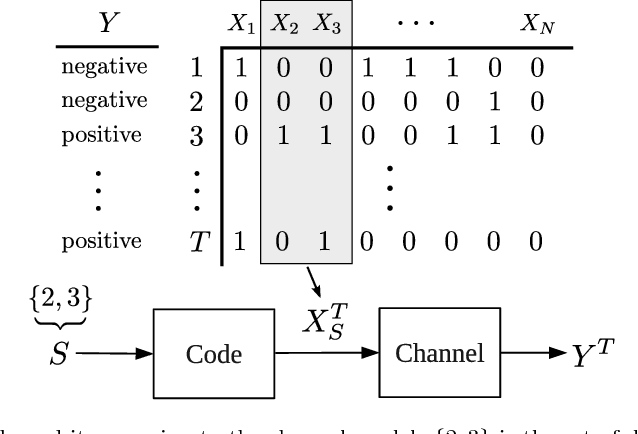
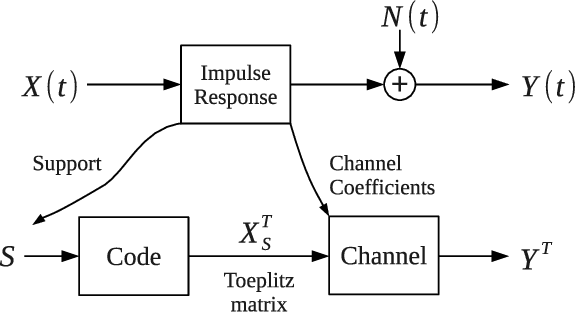
We derive fundamental sample complexity bounds for recovering sparse and structured signals for linear and nonlinear observation models including sparse regression, group testing, multivariate regression and problems with missing features. In general, sparse signal processing problems can be characterized in terms of the following Markovian property. We are given a set of $N$ variables $X_1,X_2,\ldots,X_N$, and there is an unknown subset of variables $S \subset \{1,\ldots,N\}$ that are relevant for predicting outcomes $Y$. More specifically, when $Y$ is conditioned on $\{X_n\}_{n\in S}$ it is conditionally independent of the other variables, $\{X_n\}_{n \not \in S}$. Our goal is to identify the set $S$ from samples of the variables $X$ and the associated outcomes $Y$. We characterize this problem as a version of the noisy channel coding problem. Using asymptotic information theoretic analyses, we establish mutual information formulas that provide sufficient and necessary conditions on the number of samples required to successfully recover the salient variables. These mutual information expressions unify conditions for both linear and nonlinear observations. We then compute sample complexity bounds for the aforementioned models, based on the mutual information expressions in order to demonstrate the applicability and flexibility of our results in general sparse signal processing models.

Information-Theoretic Bounds for Adaptive Sparse Recovery

We derive an information-theoretic lower bound for sample complexity in sparse recovery problems where inputs can be chosen sequentially and adaptively. This lower bound is in terms of a simple mutual information expression and unifies many different linear and nonlinear observation models. Using this formula we derive bounds for adaptive compressive sensing (CS), group testing and 1-bit CS problems. We show that adaptivity cannot decrease sample complexity in group testing, 1-bit CS and CS with linear sparsity. In contrast, we show there might be mild performance gains for CS in the sublinear regime. Our unified analysis also allows characterization of gains due to adaptivity from a wider perspective on sparse problems.

Sparse Recovery with Linear and Nonlinear Observations: Dependent and Noisy Data

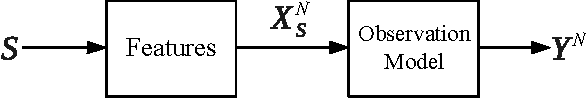
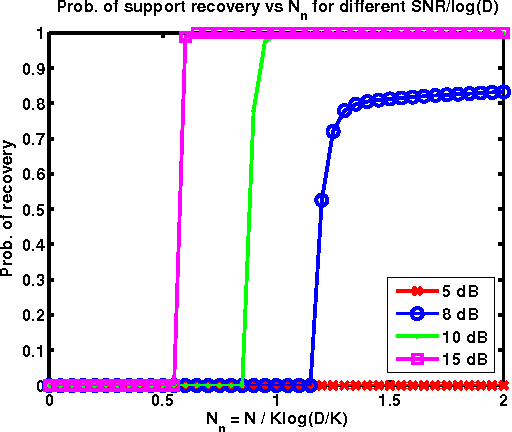
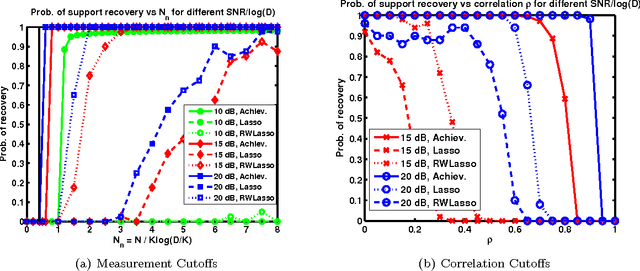
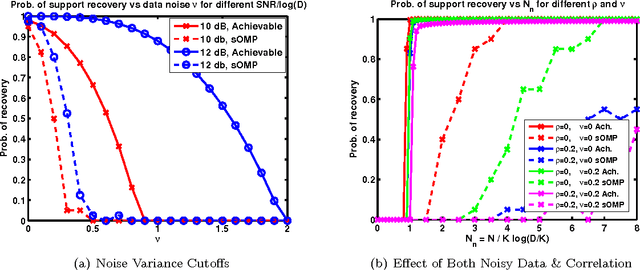
We formulate sparse support recovery as a salient set identification problem and use information-theoretic analyses to characterize the recovery performance and sample complexity. We consider a very general model where we are not restricted to linear models or specific distributions. We state non-asymptotic bounds on recovery probability and a tight mutual information formula for sample complexity. We evaluate our bounds for applications such as sparse linear regression and explicitly characterize effects of correlation or noisy features on recovery performance. We show improvements upon previous work and identify gaps between the performance of recovery algorithms and fundamental information.