Sparse Recovery with Linear and Nonlinear Observations: Dependent and Noisy Data
Paper and Code
Mar 12, 2014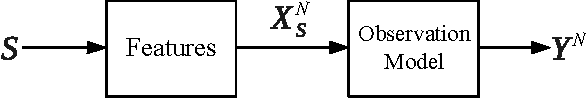
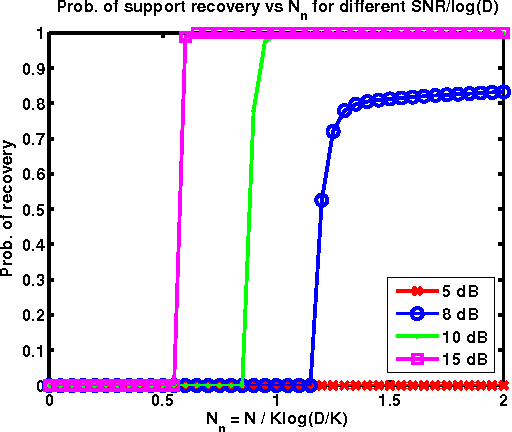
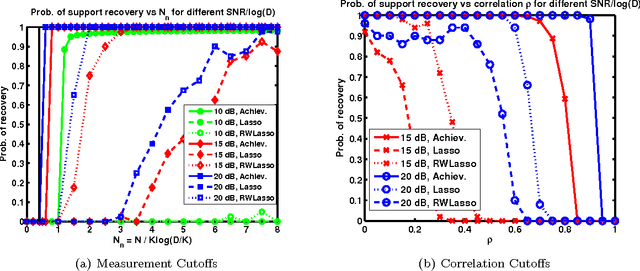
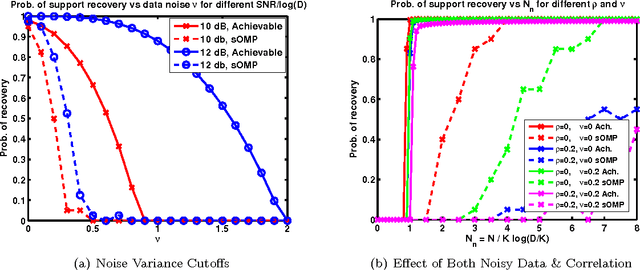
We formulate sparse support recovery as a salient set identification problem and use information-theoretic analyses to characterize the recovery performance and sample complexity. We consider a very general model where we are not restricted to linear models or specific distributions. We state non-asymptotic bounds on recovery probability and a tight mutual information formula for sample complexity. We evaluate our bounds for applications such as sparse linear regression and explicitly characterize effects of correlation or noisy features on recovery performance. We show improvements upon previous work and identify gaps between the performance of recovery algorithms and fundamental information.
* Extended version of the paper that was accepted to AISTATS 2014 as
"Information-Theoretic Characterization of Sparse Recovery". arXiv admin
note: text overlap with arXiv:1304.0682
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge