Clustering and Community Detection with Imbalanced Clusters
Paper and Code
Aug 26, 2016
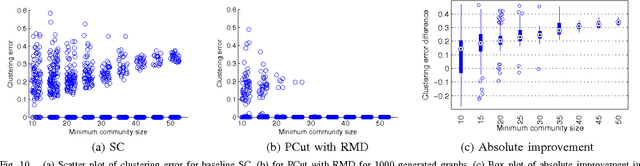
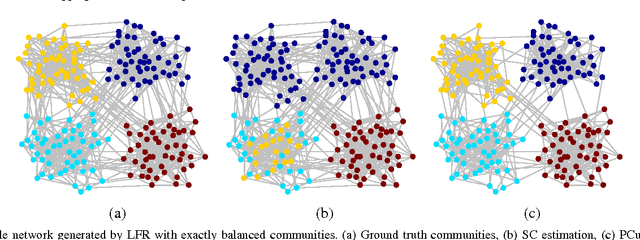
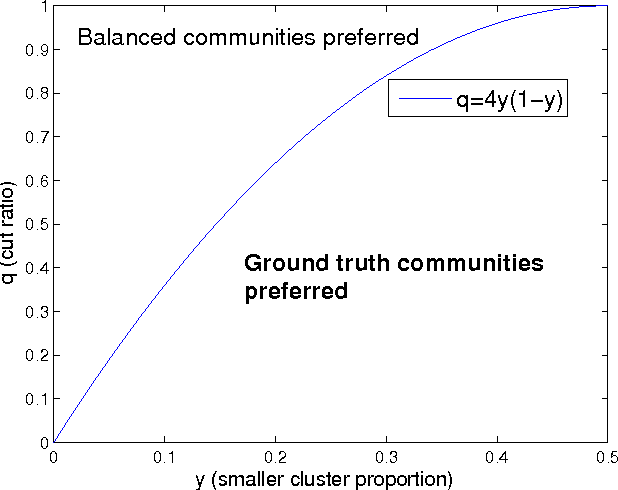
Spectral clustering methods which are frequently used in clustering and community detection applications are sensitive to the specific graph constructions particularly when imbalanced clusters are present. We show that ratio cut (RCut) or normalized cut (NCut) objectives are not tailored to imbalanced cluster sizes since they tend to emphasize cut sizes over cut values. We propose a graph partitioning problem that seeks minimum cut partitions under minimum size constraints on partitions to deal with imbalanced cluster sizes. Our approach parameterizes a family of graphs by adaptively modulating node degrees on a fixed node set, yielding a set of parameter dependent cuts reflecting varying levels of imbalance. The solution to our problem is then obtained by optimizing over these parameters. We present rigorous limit cut analysis results to justify our approach and demonstrate the superiority of our method through experiments on synthetic and real datasets for data clustering, semi-supervised learning and community detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge