Efficient Identification in Linear Structural Causal Models with Instrumental Cutsets

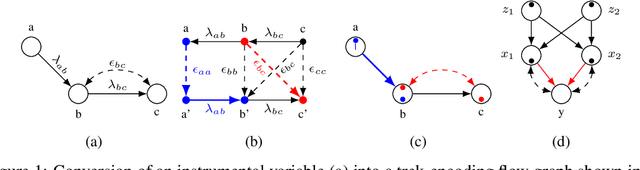
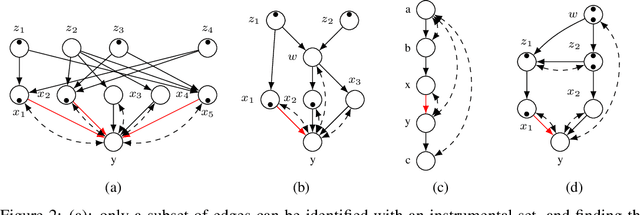
One of the most common mistakes made when performing data analysis is attributing causal meaning to regression coefficients. Formally, a causal effect can only be computed if it is identifiable from a combination of observational data and structural knowledge about the domain under investigation (Pearl, 2000, Ch. 5). Building on the literature of instrumental variables (IVs), a plethora of methods has been developed to identify causal effects in linear systems. Almost invariably, however, the most powerful such methods rely on exponential-time procedures. In this paper, we investigate graphical conditions to allow efficient identification in arbitrary linear structural causal models (SCMs). In particular, we develop a method to efficiently find unconditioned instrumental subsets, which are generalizations of IVs that can be used to tame the complexity of many canonical algorithms found in the literature. Further, we prove that determining whether an effect can be identified with TSID (Weihs et al., 2017), a method more powerful than unconditioned instrumental sets and other efficient identification algorithms, is NP-Complete. Finally, building on the idea of flow constraints, we introduce a new and efficient criterion called Instrumental Cutsets (IC), which is able to solve for parameters missed by all other existing polynomial-time algorithms.

The Hierarchy of Stable Distributions and Operators to Trade Off Stability and Performance

Recent work addressing model reliability and generalization has resulted in a variety of methods that seek to proactively address differences between the training and unknown target environments. While most methods achieve this by finding distributions that will be invariant across environments, we will show they do not necessarily find the same distributions which has implications for performance. In this paper we unify existing work on prediction using stable distributions by relating environmental shifts to edges in the graph underlying a prediction problem, and characterize stable distributions as those which effectively remove these edges. We then quantify the effect of edge deletion on performance in the linear case and corroborate the findings in a simulated and real data experiment.

Detecting Backdoor Attacks on Deep Neural Networks by Activation Clustering

While machine learning (ML) models are being increasingly trusted to make decisions in different and varying areas, the safety of systems using such models has become an increasing concern. In particular, ML models are often trained on data from potentially untrustworthy sources, providing adversaries with the opportunity to manipulate them by inserting carefully crafted samples into the training set. Recent work has shown that this type of attack, called a poisoning attack, allows adversaries to insert backdoors or trojans into the model, enabling malicious behavior with simple external backdoor triggers at inference time and only a blackbox perspective of the model itself. Detecting this type of attack is challenging because the unexpected behavior occurs only when a backdoor trigger, which is known only to the adversary, is present. Model users, either direct users of training data or users of pre-trained model from a catalog, may not guarantee the safe operation of their ML-based system. In this paper, we propose a novel approach to backdoor detection and removal for neural networks. Through extensive experimental results, we demonstrate its effectiveness for neural networks classifying text and images. To the best of our knowledge, this is the first methodology capable of detecting poisonous data crafted to insert backdoors and repairing the model that does not require a verified and trusted dataset.

Adversarial Robustness Toolbox v0.3.0

Adversarial examples have become an indisputable threat to the security of modern AI systems based on deep neural networks (DNNs). The Adversarial Robustness Toolbox (ART) is a Python library designed to support researchers and developers in creating novel defence techniques, as well as in deploying practical defences of real-world AI systems. Researchers can use ART to benchmark novel defences against the state-of-the-art. For developers, the library provides interfaces which support the composition of comprehensive defence systems using individual methods as building blocks. The Adversarial Robustness Toolbox supports machine learning models (and deep neural networks (DNNs) specifically) implemented in any of the most popular deep learning frameworks (TensorFlow, Keras, PyTorch and MXNet). Currently, the library is primarily intended to improve the adversarial robustness of visual recognition systems, however, future releases that will comprise adaptations to other data modes (such as speech, text or time series) are envisioned. The ART source code is released (https://github.com/IBM/adversarial-robustness-toolbox) under an MIT license. The release includes code examples and extensive documentation (http://adversarial-robustness-toolbox.readthedocs.io) to help researchers and developers get quickly started.

Incorporating Knowledge into Structural Equation Models using Auxiliary Variables

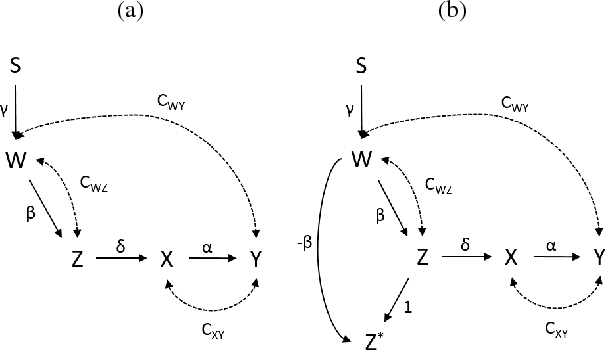
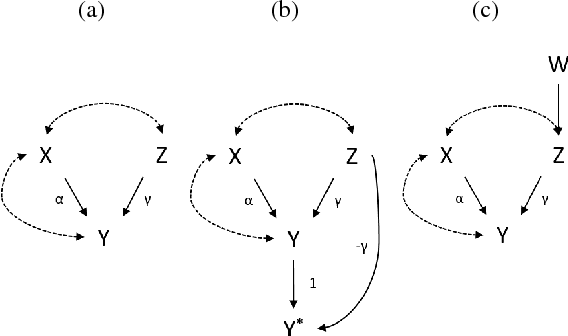
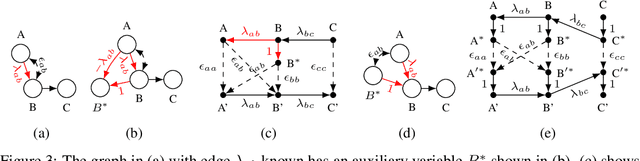
In this paper, we extend graph-based identification methods by allowing background knowledge in the form of non-zero parameter values. Such information could be obtained, for example, from a previously conducted randomized experiment, from substantive understanding of the domain, or even an identification technique. To incorporate such information systematically, we propose the addition of auxiliary variables to the model, which are constructed so that certain paths will be conveniently cancelled. This cancellation allows the auxiliary variables to help conventional methods of identification (e.g., single-door criterion, instrumental variables, half-trek criterion), as well as model testing (e.g., d-separation, over-identification). Moreover, by iteratively alternating steps of identification and adding auxiliary variables, we can improve the power of existing identification methods via a bootstrapping approach that does not require external knowledge. We operationalize this method for simple instrumental sets (a generalization of instrumental variables) and show that the resulting method is able to identify at least as many models as the most general identification method for linear systems known to date. We further discuss the application of auxiliary variables to the tasks of model testing and z-identification.

Decomposition and Identification of Linear Structural Equation Models

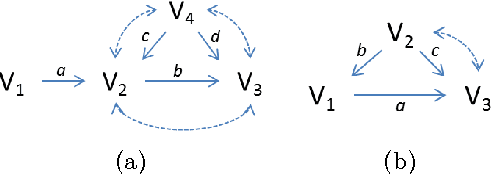
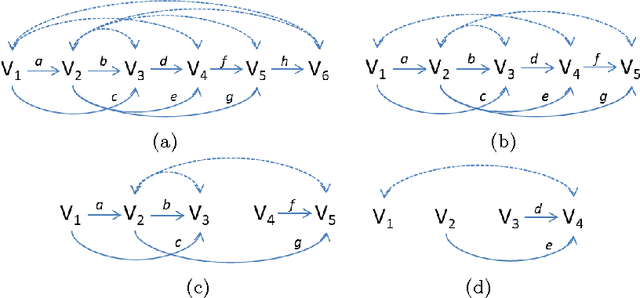
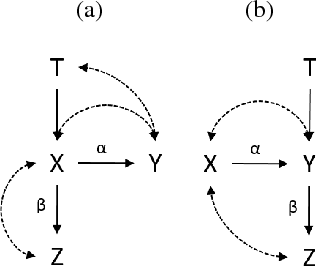
In this paper, we address the problem of identifying linear structural equation models. We first extend the edge set half-trek criterion to cover a broader class of models. We then show that any semi-Markovian linear model can be recursively decomposed into simpler sub-models, resulting in improved identification power. Finally, we show that, unlike the existing methods developed for linear models, the resulting method subsumes the identification algorithm of non-parametric models.