Variance Reduced Online Gradient Descent for Kernelized Pairwise Learning with Limited Memory

Pairwise learning is essential in machine learning, especially for problems involving loss functions defined on pairs of training examples. Online gradient descent (OGD) algorithms have been proposed to handle online pairwise learning, where data arrives sequentially. However, the pairwise nature of the problem makes scalability challenging, as the gradient computation for a new sample involves all past samples. Recent advancements in OGD algorithms have aimed to reduce the complexity of calculating online gradients, achieving complexities less than $O(T)$ and even as low as $O(1)$. However, these approaches are primarily limited to linear models and have induced variance. In this study, we propose a limited memory OGD algorithm that extends to kernel online pairwise learning while improving the sublinear regret. Specifically, we establish a clear connection between the variance of online gradients and the regret, and construct online gradients using the most recent stratified samples with a limited buffer of size of $s$ representing all past data, which have a complexity of $O(sT)$ and employs $O(\sqrt{T}\log{T})$ random Fourier features for kernel approximation. Importantly, our theoretical results demonstrate that the variance-reduced online gradients lead to an improved sublinear regret bound. The experiments on real-world datasets demonstrate the superiority of our algorithm over both kernelized and linear online pairwise learning algorithms.

Energy Efficient Training of SNN using Local Zeroth Order Method

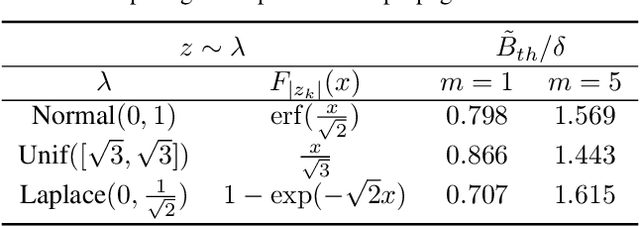
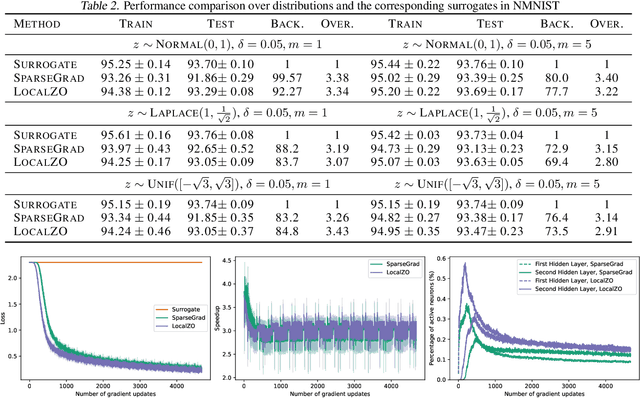
Spiking neural networks are becoming increasingly popular for their low energy requirement in real-world tasks with accuracy comparable to the traditional ANNs. SNN training algorithms face the loss of gradient information and non-differentiability due to the Heaviside function in minimizing the model loss over model parameters. To circumvent the problem surrogate method uses a differentiable approximation of the Heaviside in the backward pass, while the forward pass uses the Heaviside as the spiking function. We propose to use the zeroth order technique at the neuron level to resolve this dichotomy and use it within the automatic differentiation tool. As a result, we establish a theoretical connection between the proposed local zeroth-order technique and the existing surrogate methods and vice-versa. The proposed method naturally lends itself to energy-efficient training of SNNs on GPUs. Experimental results with neuromorphic datasets show that such implementation requires less than 1 percent neurons to be active in the backward pass, resulting in a 100x speed-up in the backward computation time. Our method offers better generalization compared to the state-of-the-art energy-efficient technique while maintaining similar efficiency.

AGGLIO: Global Optimization for Locally Convex Functions

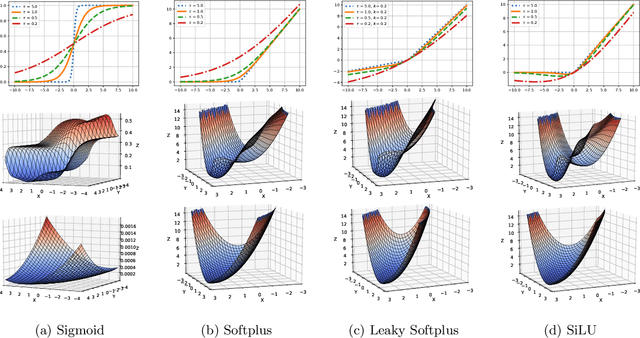
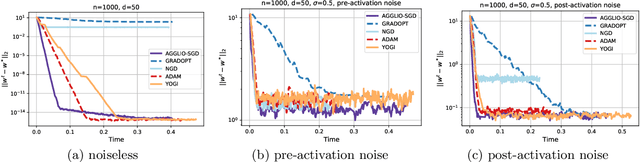
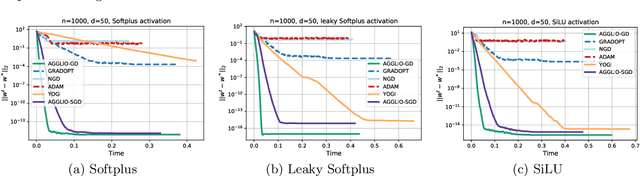
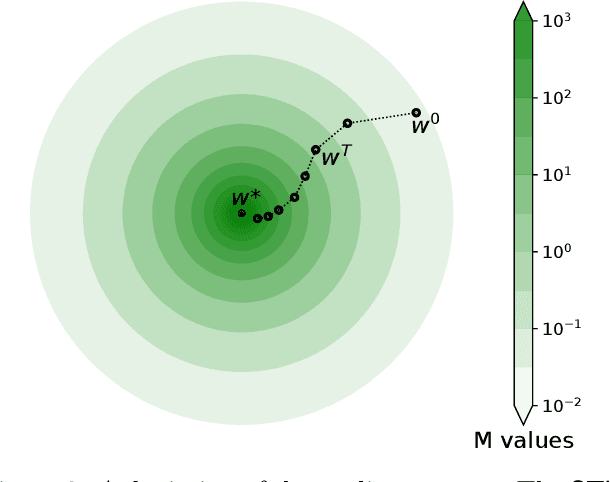
This paper presents AGGLIO (Accelerated Graduated Generalized LInear-model Optimization), a stage-wise, graduated optimization technique that offers global convergence guarantees for non-convex optimization problems whose objectives offer only local convexity and may fail to be even quasi-convex at a global scale. In particular, this includes learning problems that utilize popular activation functions such as sigmoid, softplus and SiLU that yield non-convex training objectives. AGGLIO can be readily implemented using point as well as mini-batch SGD updates and offers provable convergence to the global optimum in general conditions. In experiments, AGGLIO outperformed several recently proposed optimization techniques for non-convex and locally convex objectives in terms of convergence rate as well as convergent accuracy. AGGLIO relies on a graduation technique for generalized linear models, as well as a novel proof strategy, both of which may be of independent interest.

Globally-convergent Iteratively Reweighted Least Squares for Robust Regression Problems

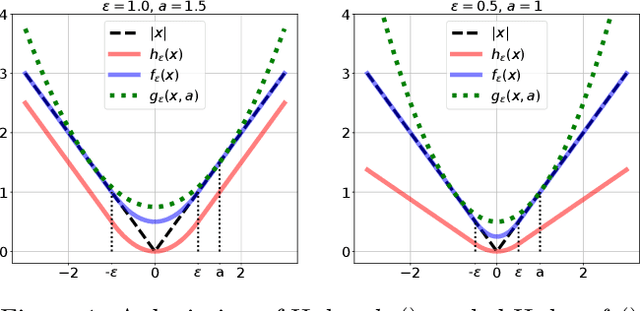
We provide the first global model recovery results for the IRLS (iteratively reweighted least squares) heuristic for robust regression problems. IRLS is known to offer excellent performance, despite bad initializations and data corruption, for several parameter estimation problems. Existing analyses of IRLS frequently require careful initialization, thus offering only local convergence guarantees. We remedy this by proposing augmentations to the basic IRLS routine that not only offer guaranteed global recovery, but in practice also outperform state-of-the-art algorithms for robust regression. Our routines are more immune to hyperparameter misspecification in basic regression tasks, as well as applied tasks such as linear-armed bandit problems. Our theoretical analyses rely on a novel extension of the notions of strong convexity and smoothness to weighted strong convexity and smoothness, and establishing that sub-Gaussian designs offer bounded weighted condition numbers. These notions may be useful in analyzing other algorithms as well.

Epidemiologically and Socio-economically Optimal Policies via Bayesian Optimization

Mass public quarantining, colloquially known as a lock-down, is a non-pharmaceutical intervention to check spread of disease. This paper presents ESOP (Epidemiologically and Socio-economically Optimal Policies), a novel application of active machine learning techniques using Bayesian optimization, that interacts with an epidemiological model to arrive at lock-down schedules that optimally balance public health benefits and socio-economic downsides of reduced economic activity during lock-down periods. The utility of ESOP is demonstrated using case studies with VIPER (Virus-Individual-Policy-EnviRonment), a stochastic agent-based simulator that this paper also proposes. However, ESOP is flexible enough to interact with arbitrary epidemiological simulators in a black-box manner, and produce schedules that involve multiple phases of lock-downs.

Model Extraction Warning in MLaaS Paradigm

Cloud vendors are increasingly offering machine learning services as part of their platform and services portfolios. These services enable the deployment of machine learning models on the cloud that are offered on a pay-per-query basis to application developers and end users. However recent work has shown that the hosted models are susceptible to extraction attacks. Adversaries may launch queries to steal the model and compromise future query payments or privacy of the training data. In this work, we present a cloud-based extraction monitor that can quantify the extraction status of models by observing the query and response streams of both individual and colluding adversarial users. We present a novel technique that uses information gain to measure the model learning rate by users with increasing number of queries. Additionally, we present an alternate technique that maintains intelligent query summaries to measure the learning rate relative to the coverage of the input feature space in the presence of collusion. Both these approaches have low computational overhead and can easily be offered as services to model owners to warn them of possible extraction attacks from adversaries. We present performance results for these approaches for decision tree models deployed on BigML MLaaS platform, using open source datasets and different adversarial attack strategies.

A Parameter-free Affinity Based Clustering

Several methods have been proposed to estimate the number of clusters in a dataset; the basic ideal behind all of them has been to study an index that measures inter-cluster separation and intra-cluster cohesion over a range of cluster numbers and report the number which gives an optimum value of the index. In this paper we propose a simple, parameter free approach that is like human cognition to form clusters, where closely lying points are easily identified to form a cluster and total number of clusters are revealed. To identify closely lying points, affinity of two points is defined as a function of distance and a threshold affinity is identified, above which two points in a dataset are likely to be in the same cluster. Well separated clusters are identified even in the presence of outliers, whereas for not so well separated dataset, final number of clusters are estimated and the detected clusters are merged to produce the final clusters. Experiments performed with several large dimensional synthetic and real datasets show good results with robustness to noise and density variation within dataset.