AGGLIO: Global Optimization for Locally Convex Functions
Paper and Code
Nov 06, 2021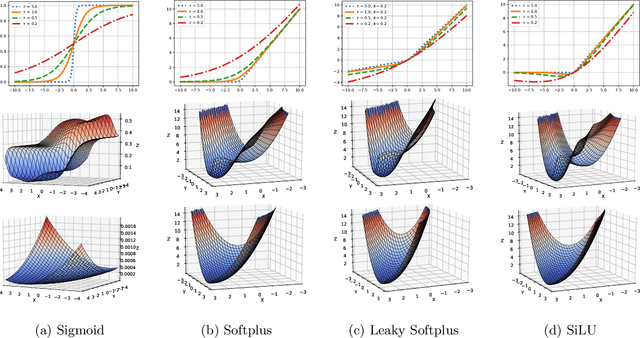

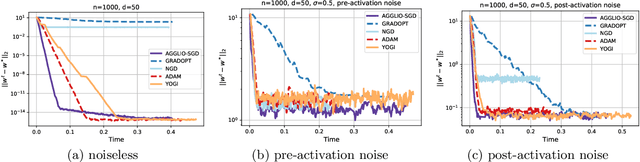
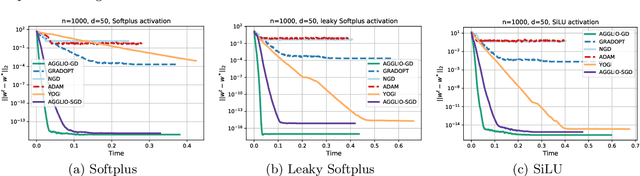
This paper presents AGGLIO (Accelerated Graduated Generalized LInear-model Optimization), a stage-wise, graduated optimization technique that offers global convergence guarantees for non-convex optimization problems whose objectives offer only local convexity and may fail to be even quasi-convex at a global scale. In particular, this includes learning problems that utilize popular activation functions such as sigmoid, softplus and SiLU that yield non-convex training objectives. AGGLIO can be readily implemented using point as well as mini-batch SGD updates and offers provable convergence to the global optimum in general conditions. In experiments, AGGLIO outperformed several recently proposed optimization techniques for non-convex and locally convex objectives in terms of convergence rate as well as convergent accuracy. AGGLIO relies on a graduation technique for generalized linear models, as well as a novel proof strategy, both of which may be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge