Corruption-tolerant Algorithms for Generalized Linear Models

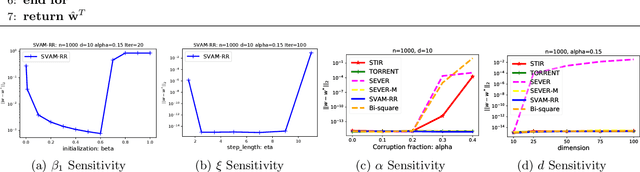
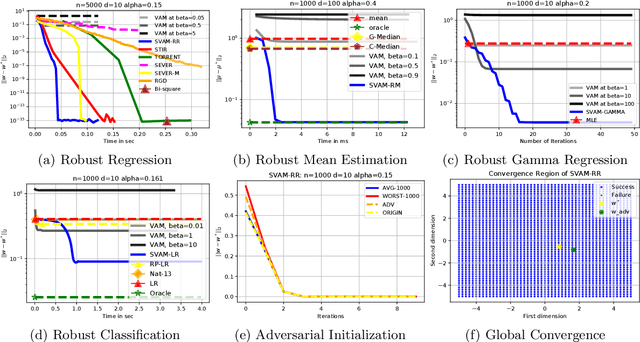
This paper presents SVAM (Sequential Variance-Altered MLE), a unified framework for learning generalized linear models under adversarial label corruption in training data. SVAM extends to tasks such as least squares regression, logistic regression, and gamma regression, whereas many existing works on learning with label corruptions focus only on least squares regression. SVAM is based on a novel variance reduction technique that may be of independent interest and works by iteratively solving weighted MLEs over variance-altered versions of the GLM objective. SVAM offers provable model recovery guarantees superior to the state-of-the-art for robust regression even when a constant fraction of training labels are adversarially corrupted. SVAM also empirically outperforms several existing problem-specific techniques for robust regression and classification. Code for SVAM is available at https://github.com/purushottamkar/svam/

AGGLIO: Global Optimization for Locally Convex Functions

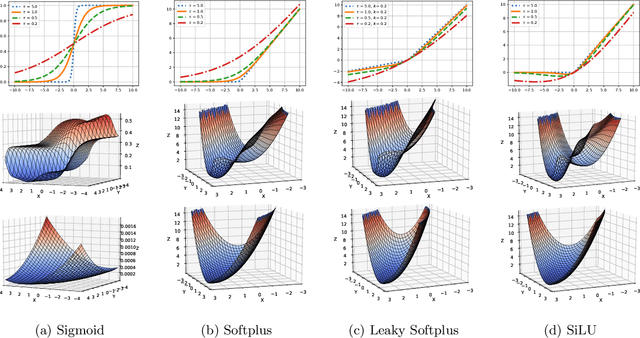
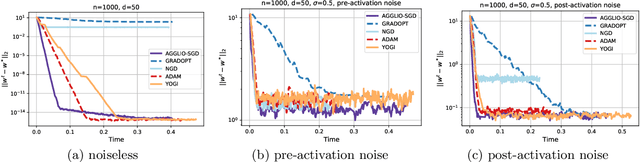
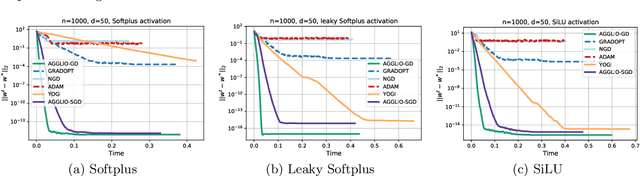
This paper presents AGGLIO (Accelerated Graduated Generalized LInear-model Optimization), a stage-wise, graduated optimization technique that offers global convergence guarantees for non-convex optimization problems whose objectives offer only local convexity and may fail to be even quasi-convex at a global scale. In particular, this includes learning problems that utilize popular activation functions such as sigmoid, softplus and SiLU that yield non-convex training objectives. AGGLIO can be readily implemented using point as well as mini-batch SGD updates and offers provable convergence to the global optimum in general conditions. In experiments, AGGLIO outperformed several recently proposed optimization techniques for non-convex and locally convex objectives in terms of convergence rate as well as convergent accuracy. AGGLIO relies on a graduation technique for generalized linear models, as well as a novel proof strategy, both of which may be of independent interest.

Epidemiologically and Socio-economically Optimal Policies via Bayesian Optimization

Mass public quarantining, colloquially known as a lock-down, is a non-pharmaceutical intervention to check spread of disease. This paper presents ESOP (Epidemiologically and Socio-economically Optimal Policies), a novel application of active machine learning techniques using Bayesian optimization, that interacts with an epidemiological model to arrive at lock-down schedules that optimally balance public health benefits and socio-economic downsides of reduced economic activity during lock-down periods. The utility of ESOP is demonstrated using case studies with VIPER (Virus-Individual-Policy-EnviRonment), a stochastic agent-based simulator that this paper also proposes. However, ESOP is flexible enough to interact with arbitrary epidemiological simulators in a black-box manner, and produce schedules that involve multiple phases of lock-downs.