Variance Reduced Online Gradient Descent for Kernelized Pairwise Learning with Limited Memory
Paper and Code
Oct 10, 2023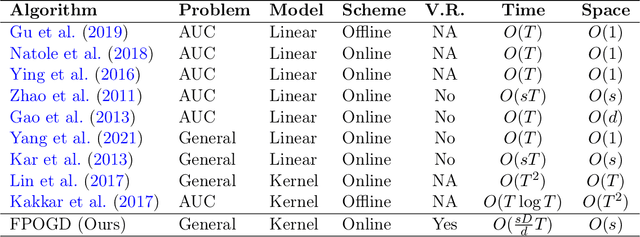
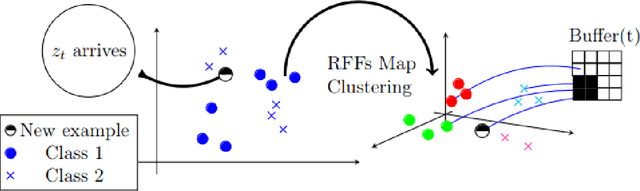
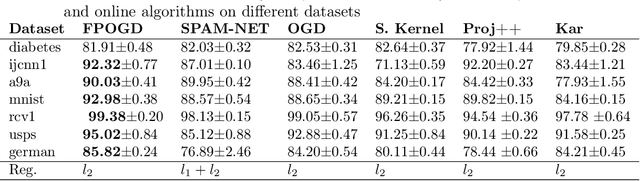
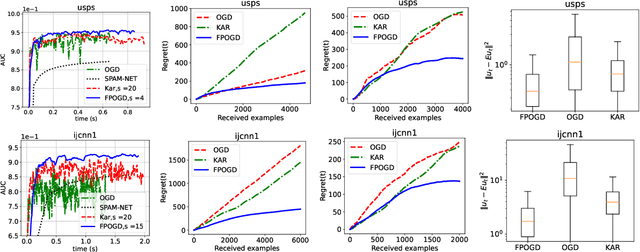
Pairwise learning is essential in machine learning, especially for problems involving loss functions defined on pairs of training examples. Online gradient descent (OGD) algorithms have been proposed to handle online pairwise learning, where data arrives sequentially. However, the pairwise nature of the problem makes scalability challenging, as the gradient computation for a new sample involves all past samples. Recent advancements in OGD algorithms have aimed to reduce the complexity of calculating online gradients, achieving complexities less than $O(T)$ and even as low as $O(1)$. However, these approaches are primarily limited to linear models and have induced variance. In this study, we propose a limited memory OGD algorithm that extends to kernel online pairwise learning while improving the sublinear regret. Specifically, we establish a clear connection between the variance of online gradients and the regret, and construct online gradients using the most recent stratified samples with a limited buffer of size of $s$ representing all past data, which have a complexity of $O(sT)$ and employs $O(\sqrt{T}\log{T})$ random Fourier features for kernel approximation. Importantly, our theoretical results demonstrate that the variance-reduced online gradients lead to an improved sublinear regret bound. The experiments on real-world datasets demonstrate the superiority of our algorithm over both kernelized and linear online pairwise learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge