Hard-Thresholding Meets Evolution Strategies in Reinforcement Learning

Evolution Strategies (ES) have emerged as a competitive alternative for model-free reinforcement learning, showcasing exemplary performance in tasks like Mujoco and Atari. Notably, they shine in scenarios with imperfect reward functions, making them invaluable for real-world applications where dense reward signals may be elusive. Yet, an inherent assumption in ES, that all input features are task-relevant, poses challenges, especially when confronted with irrelevant features common in real-world problems. This work scrutinizes this limitation, particularly focusing on the Natural Evolution Strategies (NES) variant. We propose NESHT, a novel approach that integrates Hard-Thresholding (HT) with NES to champion sparsity, ensuring only pertinent features are employed. Backed by rigorous analysis and empirical tests, NESHT demonstrates its promise in mitigating the pitfalls of irrelevant features and shines in complex decision-making problems like noisy Mujoco and Atari tasks.

Limited Memory Online Gradient Descent for Kernelized Pairwise Learning with Dynamic Averaging

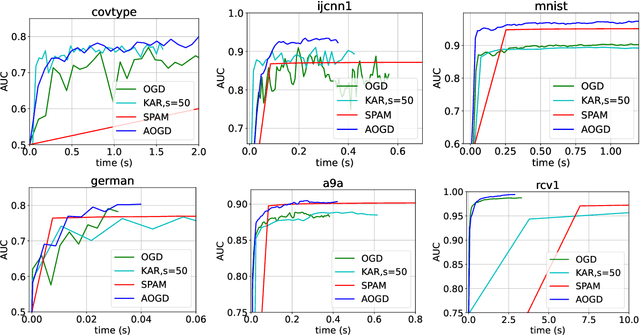
Pairwise learning, an important domain within machine learning, addresses loss functions defined on pairs of training examples, including those in metric learning and AUC maximization. Acknowledging the quadratic growth in computation complexity accompanying pairwise loss as the sample size grows, researchers have turned to online gradient descent (OGD) methods for enhanced scalability. Recently, an OGD algorithm emerged, employing gradient computation involving prior and most recent examples, a step that effectively reduces algorithmic complexity to $O(T)$, with $T$ being the number of received examples. This approach, however, confines itself to linear models while assuming the independence of example arrivals. We introduce a lightweight OGD algorithm that does not require the independence of examples and generalizes to kernel pairwise learning. Our algorithm builds the gradient based on a random example and a moving average representing the past data, which results in a sub-linear regret bound with a complexity of $O(T)$. Furthermore, through the integration of $O(\sqrt{T}{\log{T}})$ random Fourier features, the complexity of kernel calculations is effectively minimized. Several experiments with real-world datasets show that the proposed technique outperforms kernel and linear algorithms in offline and online scenarios.

Energy Efficient Training of SNN using Local Zeroth Order Method

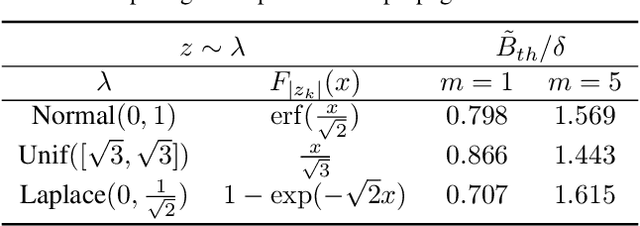
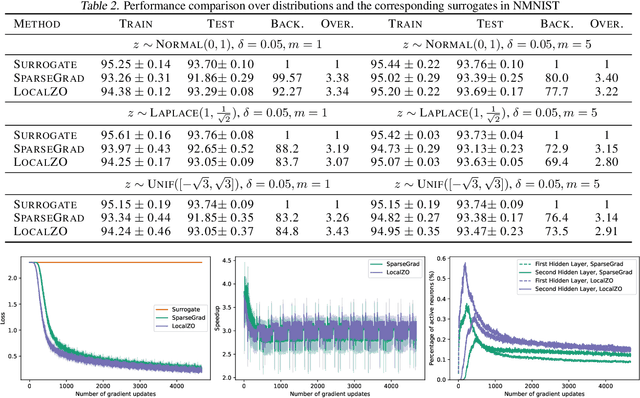
Spiking neural networks are becoming increasingly popular for their low energy requirement in real-world tasks with accuracy comparable to the traditional ANNs. SNN training algorithms face the loss of gradient information and non-differentiability due to the Heaviside function in minimizing the model loss over model parameters. To circumvent the problem surrogate method uses a differentiable approximation of the Heaviside in the backward pass, while the forward pass uses the Heaviside as the spiking function. We propose to use the zeroth order technique at the neuron level to resolve this dichotomy and use it within the automatic differentiation tool. As a result, we establish a theoretical connection between the proposed local zeroth-order technique and the existing surrogate methods and vice-versa. The proposed method naturally lends itself to energy-efficient training of SNNs on GPUs. Experimental results with neuromorphic datasets show that such implementation requires less than 1 percent neurons to be active in the backward pass, resulting in a 100x speed-up in the backward computation time. Our method offers better generalization compared to the state-of-the-art energy-efficient technique while maintaining similar efficiency.

Zeroth-Order Hard-Thresholding: Gradient Error vs. Expansivity

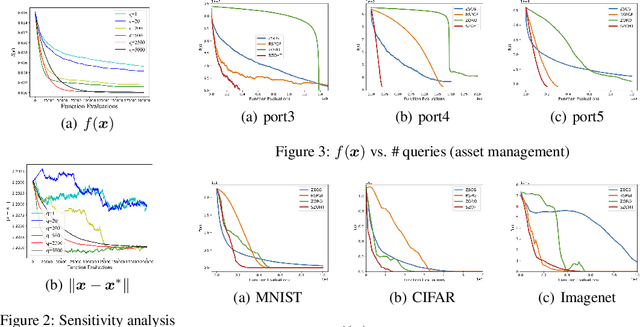
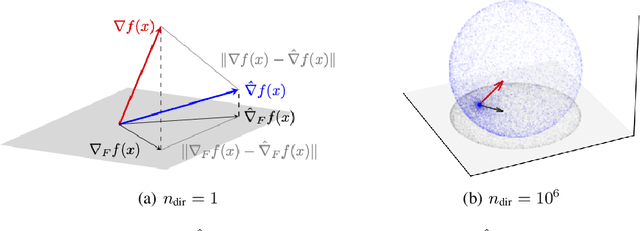
$\ell_0$ constrained optimization is prevalent in machine learning, particularly for high-dimensional problems, because it is a fundamental approach to achieve sparse learning. Hard-thresholding gradient descent is a dominant technique to solve this problem. However, first-order gradients of the objective function may be either unavailable or expensive to calculate in a lot of real-world problems, where zeroth-order (ZO) gradients could be a good surrogate. Unfortunately, whether ZO gradients can work with the hard-thresholding operator is still an unsolved problem. To solve this puzzle, in this paper, we focus on the $\ell_0$ constrained black-box stochastic optimization problems, and propose a new stochastic zeroth-order gradient hard-thresholding (SZOHT) algorithm with a general ZO gradient estimator powered by a novel random support sampling. We provide the convergence analysis of SZOHT under standard assumptions. Importantly, we reveal a conflict between the deviation of ZO estimators and the expansivity of the hard-thresholding operator, and provide a theoretical minimal value of the number of random directions in ZO gradients. In addition, we find that the query complexity of SZOHT is independent or weakly dependent on the dimensionality under different settings. Finally, we illustrate the utility of our method on a portfolio optimization problem as well as black-box adversarial attacks.

metric-learn: Metric Learning Algorithms in Python

metric-learn is an open source Python package implementing supervised and weakly-supervised distance metric learning algorithms. As part of scikit-learn-contrib, it provides a unified interface compatible with scikit-learn which allows to easily perform cross-validation, model selection, and pipelining with other machine learning estimators. metric-learn is thoroughly tested and available on PyPi under the MIT licence.