Sharper Analysis for Minibatch Stochastic Proximal Point Methods: Stability, Smoothness, and Deviation

The stochastic proximal point (SPP) methods have gained recent attention for stochastic optimization, with strong convergence guarantees and superior robustness to the classic stochastic gradient descent (SGD) methods showcased at little to no cost of computational overhead added. In this article, we study a minibatch variant of SPP, namely M-SPP, for solving convex composite risk minimization problems. The core contribution is a set of novel excess risk bounds of M-SPP derived through the lens of algorithmic stability theory. Particularly under smoothness and quadratic growth conditions, we show that M-SPP with minibatch-size $n$ and iteration count $T$ enjoys an in-expectation fast rate of convergence consisting of an $\mathcal{O}\left(\frac{1}{T^2}\right)$ bias decaying term and an $\mathcal{O}\left(\frac{1}{nT}\right)$ variance decaying term. In the small-$n$-large-$T$ setting, this result substantially improves the best known results of SPP-type approaches by revealing the impact of noise level of model on convergence rate. In the complementary small-$T$-large-$n$ regime, we provide a two-phase extension of M-SPP to achieve comparable convergence rates. Moreover, we derive a near-tight high probability (over the randomness of data) bound on the parameter estimation error of a sampling-without-replacement variant of M-SPP. Numerical evidences are provided to support our theoretical predictions when substantialized to Lasso and logistic regression models.

Zeroth-Order Hard-Thresholding: Gradient Error vs. Expansivity

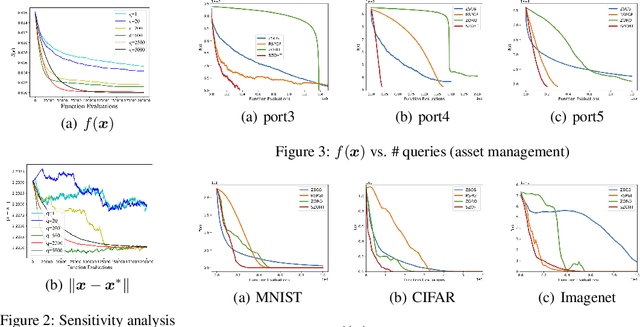
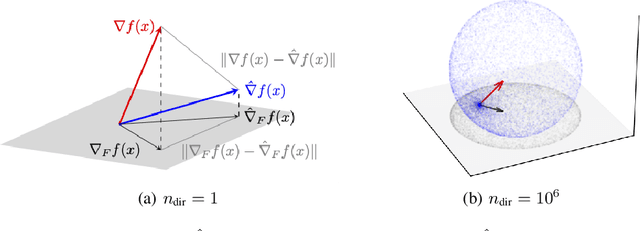
$\ell_0$ constrained optimization is prevalent in machine learning, particularly for high-dimensional problems, because it is a fundamental approach to achieve sparse learning. Hard-thresholding gradient descent is a dominant technique to solve this problem. However, first-order gradients of the objective function may be either unavailable or expensive to calculate in a lot of real-world problems, where zeroth-order (ZO) gradients could be a good surrogate. Unfortunately, whether ZO gradients can work with the hard-thresholding operator is still an unsolved problem. To solve this puzzle, in this paper, we focus on the $\ell_0$ constrained black-box stochastic optimization problems, and propose a new stochastic zeroth-order gradient hard-thresholding (SZOHT) algorithm with a general ZO gradient estimator powered by a novel random support sampling. We provide the convergence analysis of SZOHT under standard assumptions. Importantly, we reveal a conflict between the deviation of ZO estimators and the expansivity of the hard-thresholding operator, and provide a theoretical minimal value of the number of random directions in ZO gradients. In addition, we find that the query complexity of SZOHT is independent or weakly dependent on the dimensionality under different settings. Finally, we illustrate the utility of our method on a portfolio optimization problem as well as black-box adversarial attacks.

On Convergence of FedProx: Local Dissimilarity Invariant Bounds, Non-smoothness and Beyond

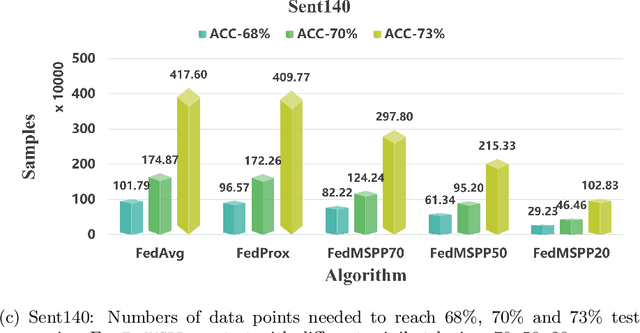
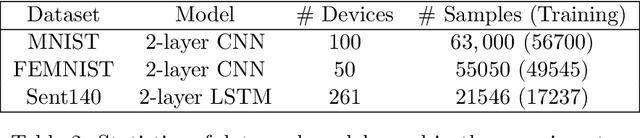
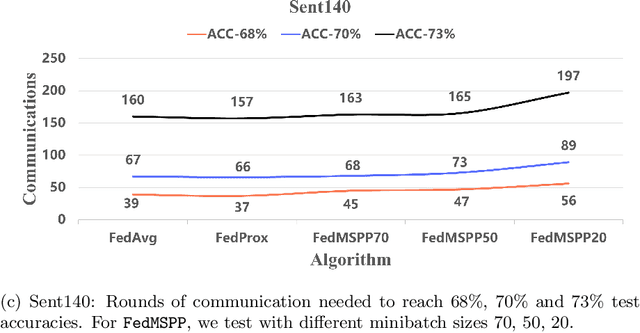
The FedProx algorithm is a simple yet powerful distributed proximal point optimization method widely used for federated learning (FL) over heterogeneous data. Despite its popularity and remarkable success witnessed in practice, the theoretical understanding of FedProx is largely underinvestigated: the appealing convergence behavior of FedProx is so far characterized under certain non-standard and unrealistic dissimilarity assumptions of local functions, and the results are limited to smooth optimization problems. In order to remedy these deficiencies, we develop a novel local dissimilarity invariant convergence theory for FedProx and its minibatch stochastic extension through the lens of algorithmic stability. As a result, we contribute to derive several new and deeper insights into FedProx for non-convex federated optimization including: 1) convergence guarantees independent on local dissimilarity type conditions; 2) convergence guarantees for non-smooth FL problems; and 3) linear speedup with respect to size of minibatch and number of sampled devices. Our theory for the first time reveals that local dissimilarity and smoothness are not must-have for FedProx to get favorable complexity bounds. Preliminary experimental results on a series of benchmark FL datasets are reported to demonstrate the benefit of minibatching for improving the sample efficiency of FedProx.

Boosting the Confidence of Generalization for $L_2$-Stable Randomized Learning Algorithms

Exponential generalization bounds with near-tight rates have recently been established for uniformly stable learning algorithms. The notion of uniform stability, however, is stringent in the sense that it is invariant to the data-generating distribution. Under the weaker and distribution dependent notions of stability such as hypothesis stability and $L_2$-stability, the literature suggests that only polynomial generalization bounds are possible in general cases. The present paper addresses this long standing tension between these two regimes of results and makes progress towards relaxing it inside a classic framework of confidence-boosting. To this end, we first establish an in-expectation first moment generalization error bound for potentially randomized learning algorithms with $L_2$-stability, based on which we then show that a properly designed subbagging process leads to near-tight exponential generalization bounds over the randomness of both data and algorithm. We further substantialize these generic results to stochastic gradient descent (SGD) to derive improved high-probability generalization bounds for convex or non-convex optimization problems with natural time decaying learning rates, which have not been possible to prove with the existing hypothesis stability or uniform stability based results.

Stability and Risk Bounds of Iterative Hard Thresholding

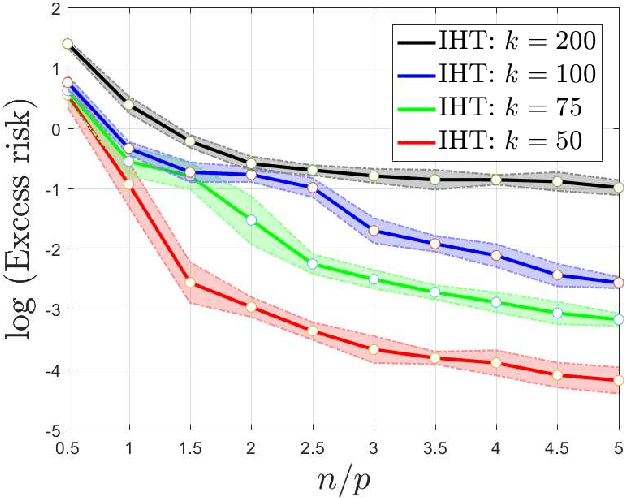
In this paper, we analyze the generalization performance of the Iterative Hard Thresholding (IHT) algorithm widely used for sparse recovery problems. The parameter estimation and sparsity recovery consistency of IHT has long been known in compressed sensing. From the perspective of statistical learning, another fundamental question is how well the IHT estimation would predict on unseen data. This paper makes progress towards answering this open question by introducing a novel sparse generalization theory for IHT under the notion of algorithmic stability. Our theory reveals that: 1) under natural conditions on the empirical risk function over $n$ samples of dimension $p$, IHT with sparsity level $k$ enjoys an $\mathcal{\tilde O}(n^{-1/2}\sqrt{k\log(n)\log(p)})$ rate of convergence in sparse excess risk; 2) a tighter $\mathcal{\tilde O}(n^{-1/2}\sqrt{\log(n)})$ bound can be established by imposing an additional iteration stability condition on a hypothetical IHT procedure invoked to the population risk; and 3) a fast rate of order $\mathcal{\tilde O}\left(n^{-1}k(\log^3(n)+\log(p))\right)$ can be derived for strongly convex risk function under proper strong-signal conditions. The results have been substantialized to sparse linear regression and sparse logistic regression models to demonstrate the applicability of our theory. Preliminary numerical evidence is provided to confirm our theoretical predictions.

A Theory-Driven Self-Labeling Refinement Method for Contrastive Representation Learning

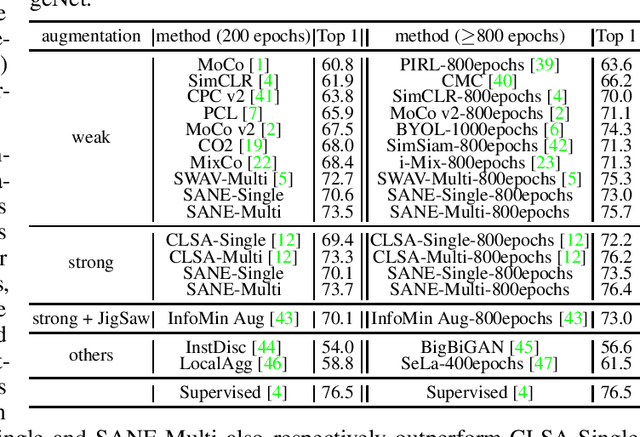
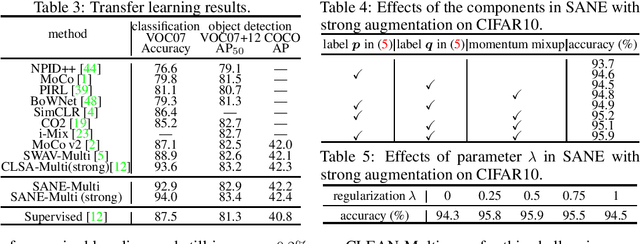
For an image query, unsupervised contrastive learning labels crops of the same image as positives, and other image crops as negatives. Although intuitive, such a native label assignment strategy cannot reveal the underlying semantic similarity between a query and its positives and negatives, and impairs performance, since some negatives are semantically similar to the query or even share the same semantic class as the query. In this work, we first prove that for contrastive learning, inaccurate label assignment heavily impairs its generalization for semantic instance discrimination, while accurate labels benefit its generalization. Inspired by this theory, we propose a novel self-labeling refinement approach for contrastive learning. It improves the label quality via two complementary modules: (i) self-labeling refinery (SLR) to generate accurate labels and (ii) momentum mixup (MM) to enhance similarity between query and its positive. SLR uses a positive of a query to estimate semantic similarity between a query and its positive and negatives, and combines estimated similarity with vanilla label assignment in contrastive learning to iteratively generate more accurate and informative soft labels. We theoretically show that our SLR can exactly recover the true semantic labels of label-corrupted data, and supervises networks to achieve zero prediction error on classification tasks. MM randomly combines queries and positives to increase semantic similarity between the generated virtual queries and their positives so as to improves label accuracy. Experimental results on CIFAR10, ImageNet, VOC and COCO show the effectiveness of our method. PyTorch code and model will be released online.

Meta-Learning with Network Pruning

Meta-learning is a powerful paradigm for few-shot learning. Although with remarkable success witnessed in many applications, the existing optimization based meta-learning models with over-parameterized neural networks have been evidenced to ovetfit on training tasks. To remedy this deficiency, we propose a network pruning based meta-learning approach for overfitting reduction via explicitly controlling the capacity of network. A uniform concentration analysis reveals the benefit of network capacity constraint for reducing generalization gap of the proposed meta-learner. We have implemented our approach on top of Reptile assembled with two network pruning routines: Dense-Sparse-Dense (DSD) and Iterative Hard Thresholding (IHT). Extensive experimental results on benchmark datasets with different over-parameterized deep networks demonstrate that our method not only effectively alleviates meta-overfitting but also in many cases improves the overall generalization performance when applied to few-shot classification tasks.

On Convergence of Distributed Approximate Newton Methods: Globalization, Sharper Bounds and Beyond

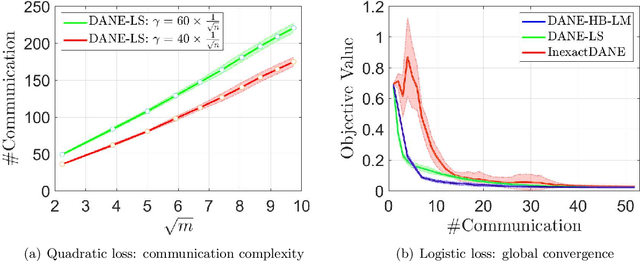
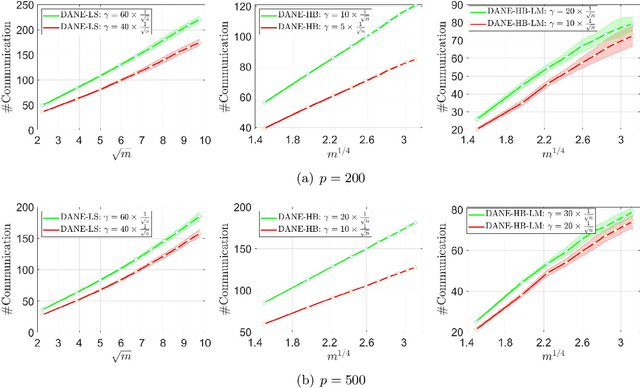
The DANE algorithm is an approximate Newton method popularly used for communication-efficient distributed machine learning. Reasons for the interest in DANE include scalability and versatility. Convergence of DANE, however, can be tricky; its appealing convergence rate is only rigorous for quadratic objective, and for more general convex functions the known results are no stronger than those of the classic first-order methods. To remedy these drawbacks, we propose in this paper some new alternatives of DANE which are more suitable for analysis. We first introduce a simple variant of DANE equipped with backtracking line search, for which global asymptotic convergence and sharper local non-asymptotic convergence rate guarantees can be proved for both quadratic and non-quadratic strongly convex functions. Then we propose a heavy-ball method to accelerate the convergence of DANE, showing that nearly tight local rate of convergence can be established for strongly convex functions, and with proper modification of algorithm the same result applies globally to linear prediction models. Numerical evidence is provided to confirm the theoretical and practical advantages of our methods.

Dual Iterative Hard Thresholding: From Non-convex Sparse Minimization to Non-smooth Concave Maximization

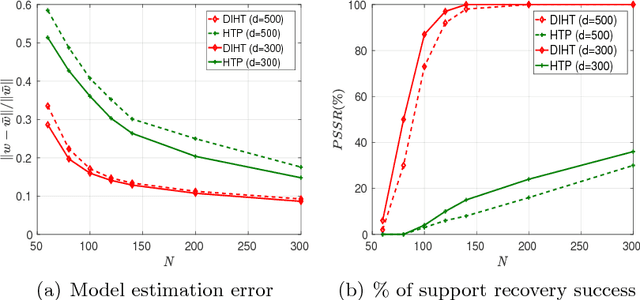
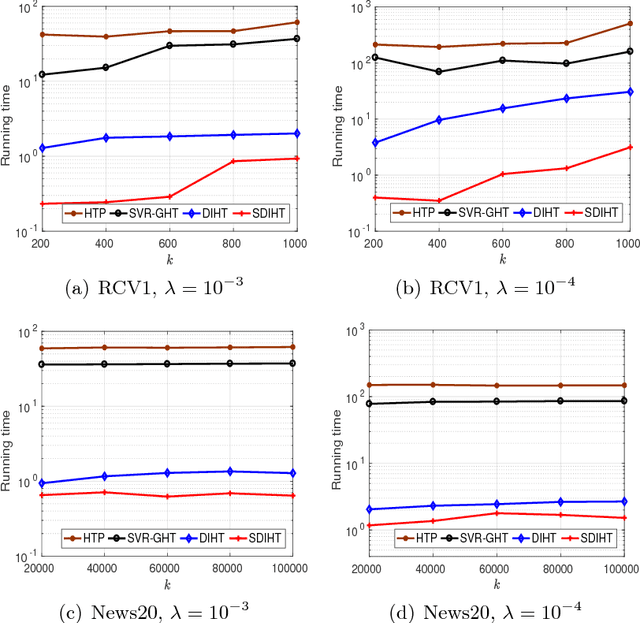
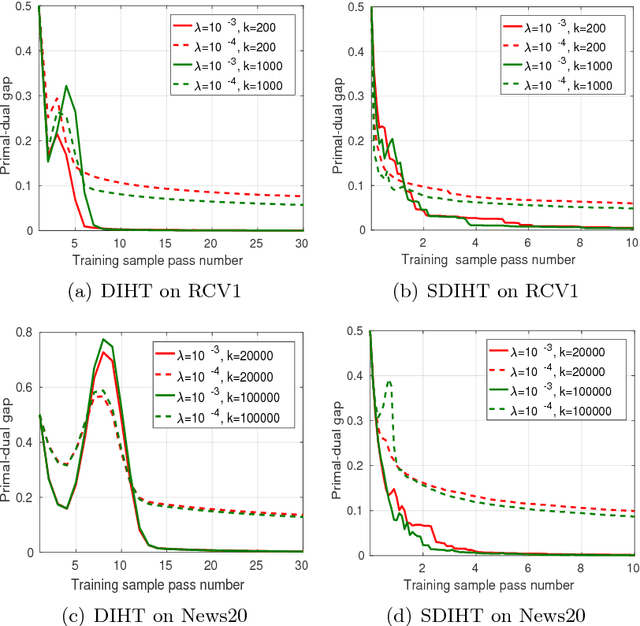
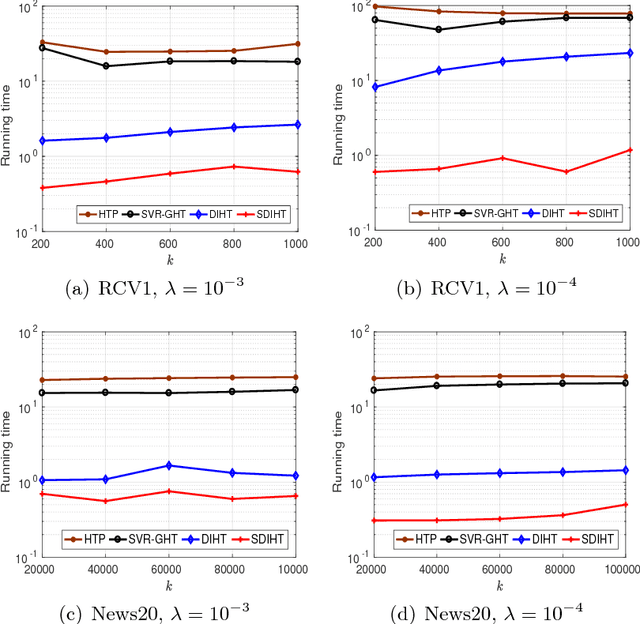
Iterative Hard Thresholding (IHT) is a class of projected gradient descent methods for optimizing sparsity-constrained minimization models, with the best known efficiency and scalability in practice. As far as we know, the existing IHT-style methods are designed for sparse minimization in primal form. It remains open to explore duality theory and algorithms in such a non-convex and NP-hard problem setting. In this paper, we bridge this gap by establishing a duality theory for sparsity-constrained minimization with $\ell_2$-regularized loss function and proposing an IHT-style algorithm for dual maximization. Our sparse duality theory provides a set of sufficient and necessary conditions under which the original NP-hard/non-convex problem can be equivalently solved in a dual formulation. The proposed dual IHT algorithm is a super-gradient method for maximizing the non-smooth dual objective. An interesting finding is that the sparse recovery performance of dual IHT is invariant to the Restricted Isometry Property (RIP), which is required by virtually all the existing primal IHT algorithms without sparsity relaxation. Moreover, a stochastic variant of dual IHT is proposed for large-scale stochastic optimization. Numerical results demonstrate the superiority of dual IHT algorithms to the state-of-the-art primal IHT-style algorithms in model estimation accuracy and computational efficiency.

Gradient Hard Thresholding Pursuit for Sparsity-Constrained Optimization

Hard Thresholding Pursuit (HTP) is an iterative greedy selection procedure for finding sparse solutions of underdetermined linear systems. This method has been shown to have strong theoretical guarantee and impressive numerical performance. In this paper, we generalize HTP from compressive sensing to a generic problem setup of sparsity-constrained convex optimization. The proposed algorithm iterates between a standard gradient descent step and a hard thresholding step with or without debiasing. We prove that our method enjoys the strong guarantees analogous to HTP in terms of rate of convergence and parameter estimation accuracy. Numerical evidences show that our method is superior to the state-of-the-art greedy selection methods in sparse logistic regression and sparse precision matrix estimation tasks.