Obtaining Lower Query Complexities through Lightweight Zeroth-Order Proximal Gradient Algorithms

Zeroth-order (ZO) optimization is one key technique for machine learning problems where gradient calculation is expensive or impossible. Several variance reduced ZO proximal algorithms have been proposed to speed up ZO optimization for non-smooth problems, and all of them opted for the coordinated ZO estimator against the random ZO estimator when approximating the true gradient, since the former is more accurate. While the random ZO estimator introduces bigger error and makes convergence analysis more challenging compared to coordinated ZO estimator, it requires only $\mathcal{O}(1)$ computation, which is significantly less than $\mathcal{O}(d)$ computation of the coordinated ZO estimator, with $d$ being dimension of the problem space. To take advantage of the computationally efficient nature of the random ZO estimator, we first propose a ZO objective decrease (ZOOD) property which can incorporate two different types of errors in the upper bound of convergence rate. Next, we propose two generic reduction frameworks for ZO optimization which can automatically derive the convergence results for convex and non-convex problems respectively, as long as the convergence rate for the inner solver satisfies the ZOOD property. With the application of two reduction frameworks on our proposed ZOR-ProxSVRG and ZOR-ProxSAGA, two variance reduced ZO proximal algorithms with fully random ZO estimators, we improve the state-of-the-art function query complexities from $\mathcal{O}\left(\min\{\frac{dn^{1/2}}{\epsilon^2}, \frac{d}{\epsilon^3}\}\right)$ to $\tilde{\mathcal{O}}\left(\frac{n+d}{\epsilon^2}\right)$ under $d > n^{\frac{1}{2}}$ for non-convex problems, and from $\mathcal{O}\left(\frac{d}{\epsilon^2}\right)$ to $\tilde{\mathcal{O}}\left(n\log\frac{1}{\epsilon}+\frac{d}{\epsilon}\right)$ for convex problems.

Hard-Thresholding Meets Evolution Strategies in Reinforcement Learning

Evolution Strategies (ES) have emerged as a competitive alternative for model-free reinforcement learning, showcasing exemplary performance in tasks like Mujoco and Atari. Notably, they shine in scenarios with imperfect reward functions, making them invaluable for real-world applications where dense reward signals may be elusive. Yet, an inherent assumption in ES, that all input features are task-relevant, poses challenges, especially when confronted with irrelevant features common in real-world problems. This work scrutinizes this limitation, particularly focusing on the Natural Evolution Strategies (NES) variant. We propose NESHT, a novel approach that integrates Hard-Thresholding (HT) with NES to champion sparsity, ensuring only pertinent features are employed. Backed by rigorous analysis and empirical tests, NESHT demonstrates its promise in mitigating the pitfalls of irrelevant features and shines in complex decision-making problems like noisy Mujoco and Atari tasks.

Zeroth-Order Hard-Thresholding: Gradient Error vs. Expansivity

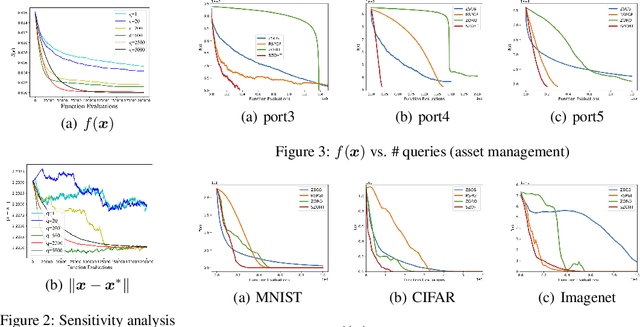
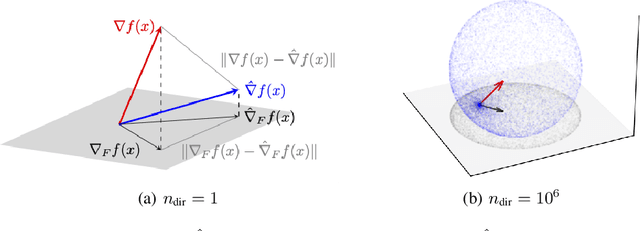
$\ell_0$ constrained optimization is prevalent in machine learning, particularly for high-dimensional problems, because it is a fundamental approach to achieve sparse learning. Hard-thresholding gradient descent is a dominant technique to solve this problem. However, first-order gradients of the objective function may be either unavailable or expensive to calculate in a lot of real-world problems, where zeroth-order (ZO) gradients could be a good surrogate. Unfortunately, whether ZO gradients can work with the hard-thresholding operator is still an unsolved problem. To solve this puzzle, in this paper, we focus on the $\ell_0$ constrained black-box stochastic optimization problems, and propose a new stochastic zeroth-order gradient hard-thresholding (SZOHT) algorithm with a general ZO gradient estimator powered by a novel random support sampling. We provide the convergence analysis of SZOHT under standard assumptions. Importantly, we reveal a conflict between the deviation of ZO estimators and the expansivity of the hard-thresholding operator, and provide a theoretical minimal value of the number of random directions in ZO gradients. In addition, we find that the query complexity of SZOHT is independent or weakly dependent on the dimensionality under different settings. Finally, we illustrate the utility of our method on a portfolio optimization problem as well as black-box adversarial attacks.

Zeroth-Order Negative Curvature Finding: Escaping Saddle Points without Gradients

We consider escaping saddle points of nonconvex problems where only the function evaluations can be accessed. Although a variety of works have been proposed, the majority of them require either second or first-order information, and only a few of them have exploited zeroth-order methods, particularly the technique of negative curvature finding with zeroth-order methods which has been proven to be the most efficient method for escaping saddle points. To fill this gap, in this paper, we propose two zeroth-order negative curvature finding frameworks that can replace Hessian-vector product computations without increasing the iteration complexity. We apply the proposed frameworks to ZO-GD, ZO-SGD, ZO-SCSG, ZO-SPIDER and prove that these ZO algorithms can converge to $(\epsilon,\delta)$-approximate second-order stationary points with less query complexity compared with prior zeroth-order works for finding local minima.