Limited Memory Online Gradient Descent for Kernelized Pairwise Learning with Dynamic Averaging
Paper and Code
Feb 02, 2024
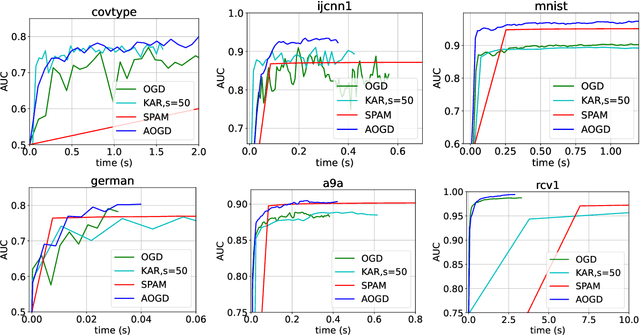

Pairwise learning, an important domain within machine learning, addresses loss functions defined on pairs of training examples, including those in metric learning and AUC maximization. Acknowledging the quadratic growth in computation complexity accompanying pairwise loss as the sample size grows, researchers have turned to online gradient descent (OGD) methods for enhanced scalability. Recently, an OGD algorithm emerged, employing gradient computation involving prior and most recent examples, a step that effectively reduces algorithmic complexity to $O(T)$, with $T$ being the number of received examples. This approach, however, confines itself to linear models while assuming the independence of example arrivals. We introduce a lightweight OGD algorithm that does not require the independence of examples and generalizes to kernel pairwise learning. Our algorithm builds the gradient based on a random example and a moving average representing the past data, which results in a sub-linear regret bound with a complexity of $O(T)$. Furthermore, through the integration of $O(\sqrt{T}{\log{T}})$ random Fourier features, the complexity of kernel calculations is effectively minimized. Several experiments with real-world datasets show that the proposed technique outperforms kernel and linear algorithms in offline and online scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge