Position Paper: Bayesian Deep Learning in the Age of Large-Scale AI

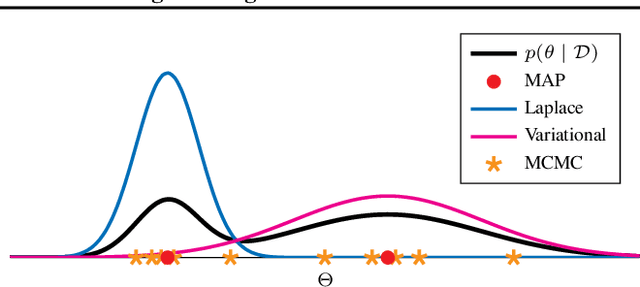
In the current landscape of deep learning research, there is a predominant emphasis on achieving high predictive accuracy in supervised tasks involving large image and language datasets. However, a broader perspective reveals a multitude of overlooked metrics, tasks, and data types, such as uncertainty, active and continual learning, and scientific data, that demand attention. Bayesian deep learning (BDL) constitutes a promising avenue, offering advantages across these diverse settings. This paper posits that BDL can elevate the capabilities of deep learning. It revisits the strengths of BDL, acknowledges existing challenges, and highlights some exciting research avenues aimed at addressing these obstacles. Looking ahead, the discussion focuses on possible ways to combine large-scale foundation models with BDL to unlock their full potential.

Sparsifying Bayesian neural networks with latent binary variables and normalizing flows

Artificial neural networks (ANNs) are powerful machine learning methods used in many modern applications such as facial recognition, machine translation, and cancer diagnostics. A common issue with ANNs is that they usually have millions or billions of trainable parameters, and therefore tend to overfit to the training data. This is especially problematic in applications where it is important to have reliable uncertainty estimates. Bayesian neural networks (BNN) can improve on this, since they incorporate parameter uncertainty. In addition, latent binary Bayesian neural networks (LBBNN) also take into account structural uncertainty by allowing the weights to be turned on or off, enabling inference in the joint space of weights and structures. In this paper, we will consider two extensions to the LBBNN method: Firstly, by using the local reparametrization trick (LRT) to sample the hidden units directly, we get a more computationally efficient algorithm. More importantly, by using normalizing flows on the variational posterior distribution of the LBBNN parameters, the network learns a more flexible variational posterior distribution than the mean field Gaussian. Experimental results show that this improves predictive power compared to the LBBNN method, while also obtaining more sparse networks. We perform two simulation studies. In the first study, we consider variable selection in a logistic regression setting, where the more flexible variational distribution leads to improved results. In the second study, we compare predictive uncertainty based on data generated from two-dimensional Gaussian distributions. Here, we argue that our Bayesian methods lead to more realistic estimates of predictive uncertainty.

Variational Inference for Bayesian Neural Networks under Model and Parameter Uncertainty

Bayesian neural networks (BNNs) have recently regained a significant amount of attention in the deep learning community due to the development of scalable approximate Bayesian inference techniques. There are several advantages of using a Bayesian approach: Parameter and prediction uncertainties become easily available, facilitating rigorous statistical analysis. Furthermore, prior knowledge can be incorporated. However, so far, there have been no scalable techniques capable of combining both structural and parameter uncertainty. In this paper, we apply the concept of model uncertainty as a framework for structural learning in BNNs and hence make inference in the joint space of structures/models and parameters. Moreover, we suggest an adaptation of a scalable variational inference approach with reparametrization of marginal inclusion probabilities to incorporate the model space constraints. Experimental results on a range of benchmark datasets show that we obtain comparable accuracy results with the competing models, but based on methods that are much more sparse than ordinary BNNs.

Reversible Genetically Modified Mode Jumping MCMC

In this paper, we introduce a reversible version of a genetically modified mode jumping Markov chain Monte Carlo algorithm (GMJMCMC) for inference on posterior model probabilities in complex model spaces, where the number of explanatory variables is prohibitively large for classical Markov Chain Monte Carlo methods. Unlike the earlier proposed GMJMCMC algorithm, the introduced algorithm is a proper MCMC and its limiting distribution corresponds to the posterior marginal model probabilities in the explored model space under reasonable regularity conditions.

Reversible Genetically Modified ModeJumping MCMC

In this paper, we introduce a reversible version of a genetically modified mode jumping Markov chain Monte Carlo algorithm (GMJMCMC) for inference on posterior model probabilities in complex model spaces, where the number of explanatory variables is prohibitively large for classical Markov Chain Monte Carlo methods. Unlike the earlier proposed GMJMCMC algorithm, the introduced algorithm is a proper MCMC and its limiting distribution corresponds to the posterior marginal model probabilities in the explored model space under reasonable regularity conditions.

skweak: Weak Supervision Made Easy for NLP

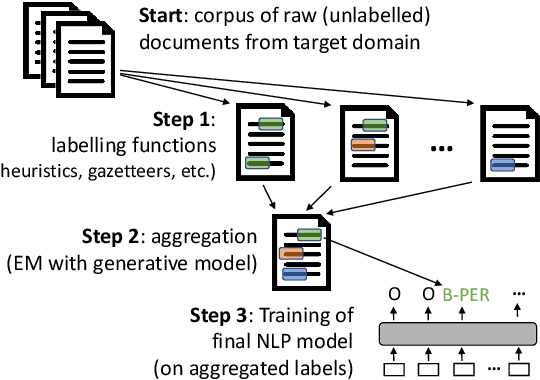
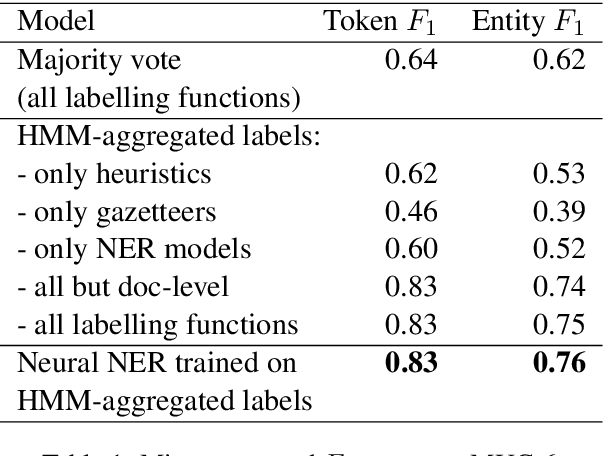
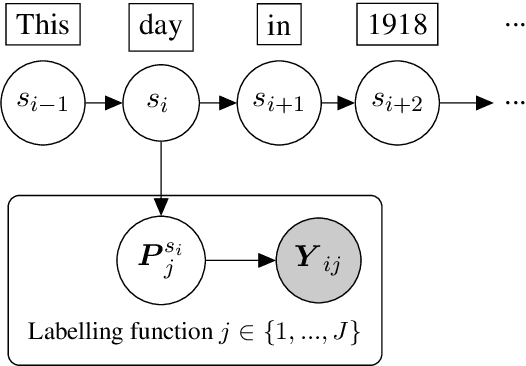
We present skweak, a versatile, Python-based software toolkit enabling NLP developers to apply weak supervision to a wide range of NLP tasks. Weak supervision is an emerging machine learning paradigm based on a simple idea: instead of labelling data points by hand, we use labelling functions derived from domain knowledge to automatically obtain annotations for a given dataset. The resulting labels are then aggregated with a generative model that estimates the accuracy (and possible confusions) of each labelling function. The skweak toolkit makes it easy to implement a large spectrum of labelling functions (such as heuristics, gazetteers, neural models or linguistic constraints) on text data, apply them on a corpus, and aggregate their results in a fully unsupervised fashion. skweak is especially designed to facilitate the use of weak supervision for NLP tasks such as text classification and sequence labelling. We illustrate the use of skweak for NER and sentiment analysis. skweak is released under an open-source license and is available at: https://github.com/NorskRegnesentral/skweak

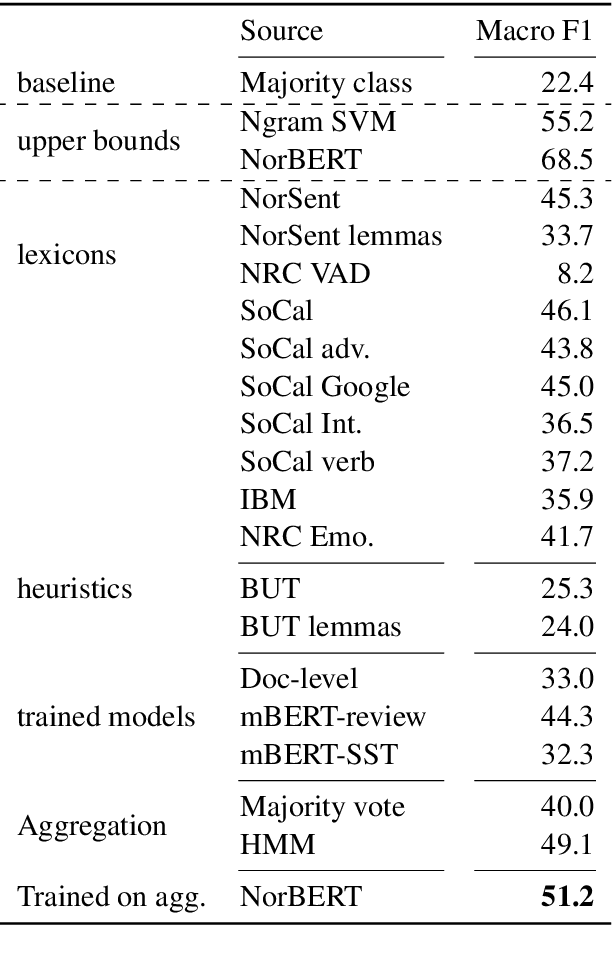
Rejoinder for the discussion of the paper "A novel algorithmic approach to Bayesian Logic Regression"

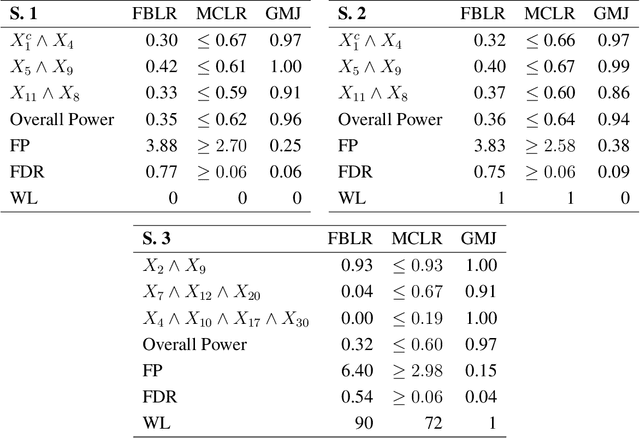
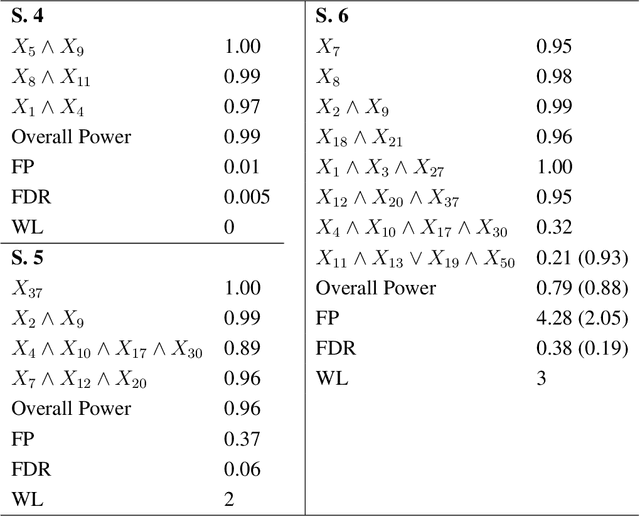
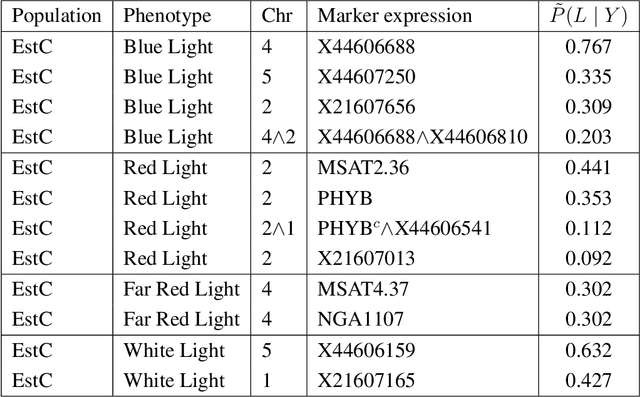
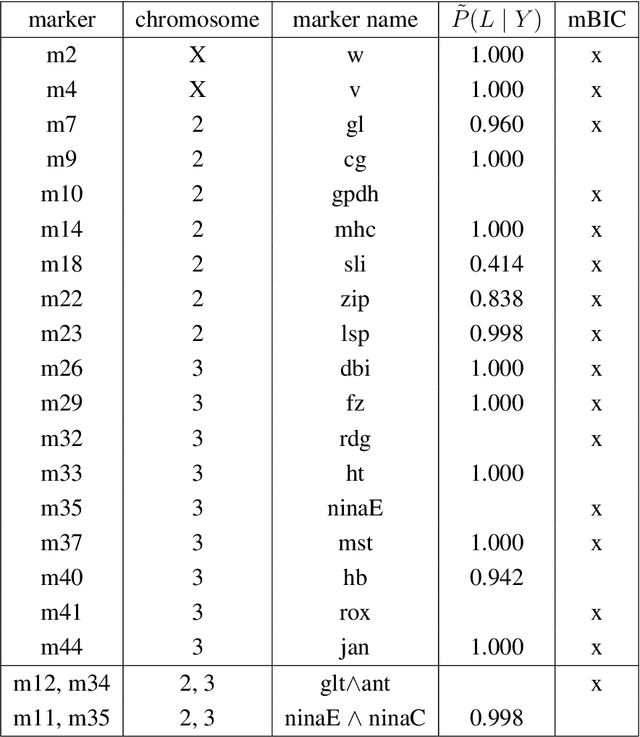
In this rejoinder we summarize the comments, questions and remarks on the paper "A novel algorithmic approach to Bayesian Logic Regression" from the discussants. We then respond to those comments, questions and remarks, provide several extensions of the original model and give a tutorial on our R-package EMJMCMC (http://aliaksah.github.io/EMJMCMC2016/)

Named Entity Recognition without Labelled Data: A Weak Supervision Approach

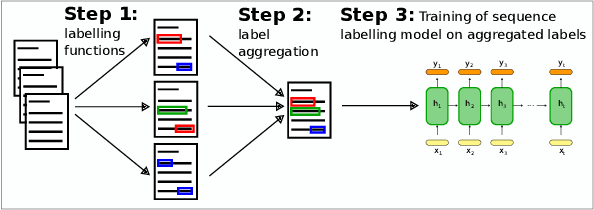
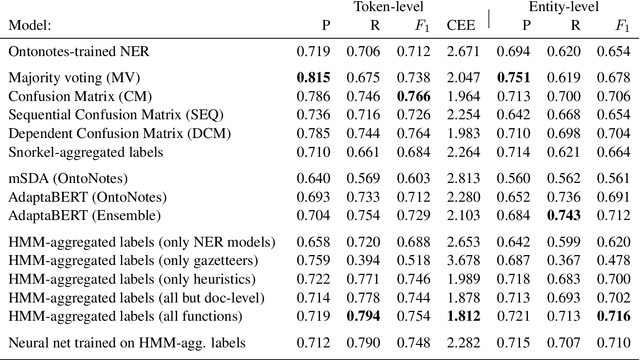
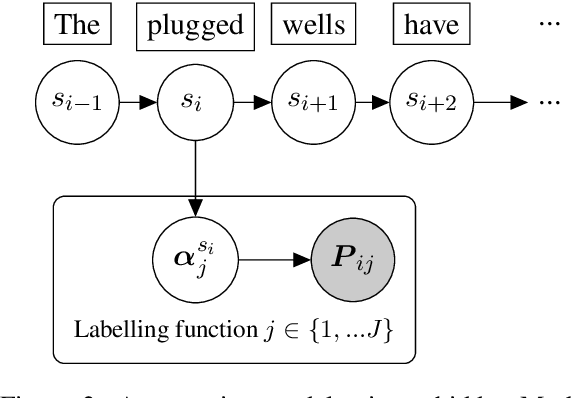
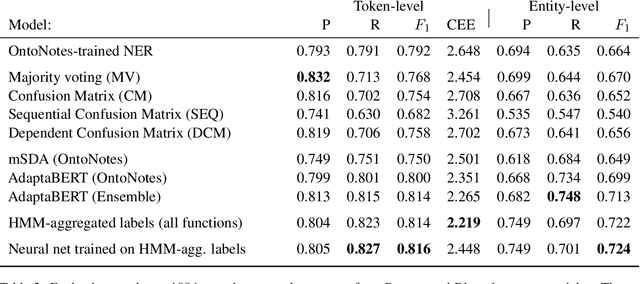
Named Entity Recognition (NER) performance often degrades rapidly when applied to target domains that differ from the texts observed during training. When in-domain labelled data is available, transfer learning techniques can be used to adapt existing NER models to the target domain. But what should one do when there is no hand-labelled data for the target domain? This paper presents a simple but powerful approach to learn NER models in the absence of labelled data through weak supervision. The approach relies on a broad spectrum of labelling functions to automatically annotate texts from the target domain. These annotations are then merged together using a hidden Markov model which captures the varying accuracies and confusions of the labelling functions. A sequence labelling model can finally be trained on the basis of this unified annotation. We evaluate the approach on two English datasets (CoNLL 2003 and news articles from Reuters and Bloomberg) and demonstrate an improvement of about 7 percentage points in entity-level $F_1$ scores compared to an out-of-domain neural NER model.

Flexible Bayesian Nonlinear Model Configuration

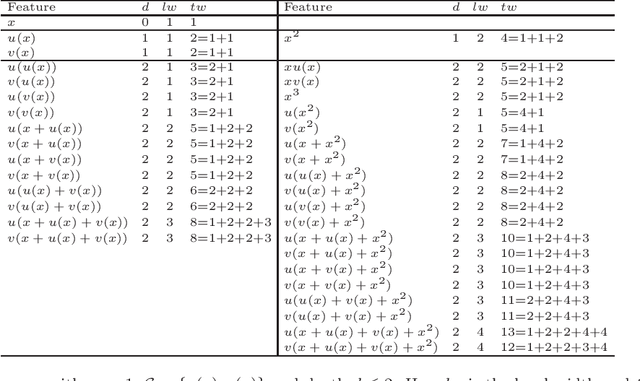
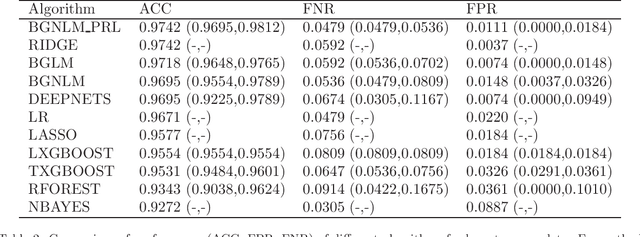
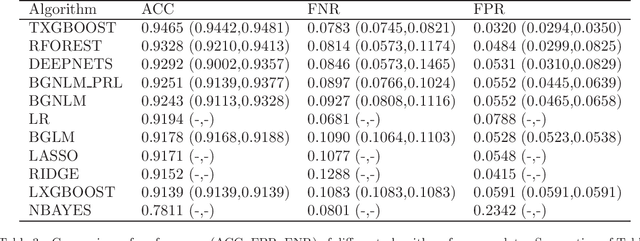
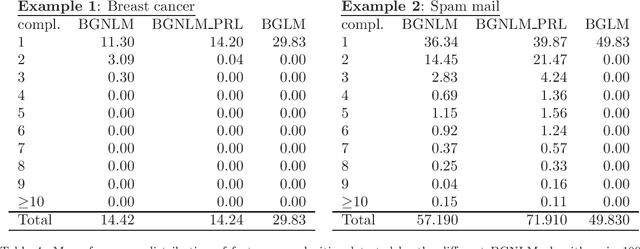
Regression models are used in a wide range of applications providing a powerful scientific tool for researchers from different fields. Linear models are often not sufficient to describe the complex relationship between input variables and a response. This relationship can be better described by non-linearities and complex functional interactions. Deep learning models have been extremely successful in terms of prediction although they are often difficult to specify and potentially suffer from overfitting. In this paper, we introduce a class of Bayesian generalized nonlinear regression models with a comprehensive non-linear feature space. Non-linear features are generated hierarchically, similarly to deep learning, but have additional flexibility on the possible types of features to be considered. This flexibility, combined with variable selection, allows us to find a small set of important features and thereby more interpretable models. A genetically modified Markov chain Monte Carlo algorithm is developed to make inference. Model averaging is also possible within our framework. In various applications, we illustrate how our approach is used to obtain meaningful non-linear models. Additionally, we compare its predictive performance with a number of machine learning algorithms.