Flexible Bayesian Nonlinear Model Configuration

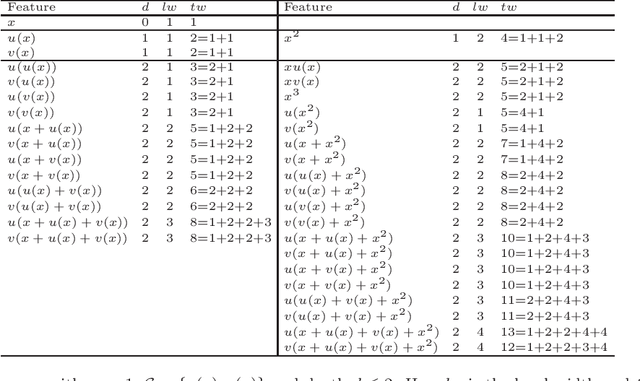
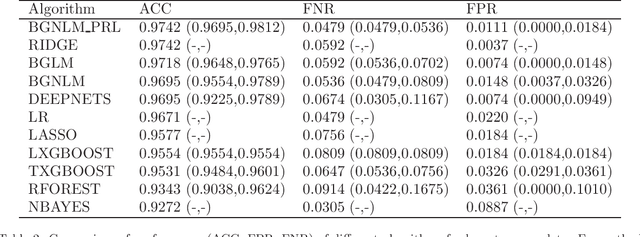
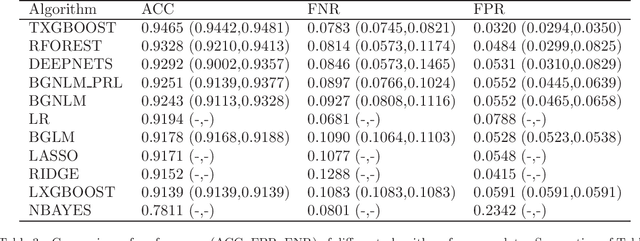
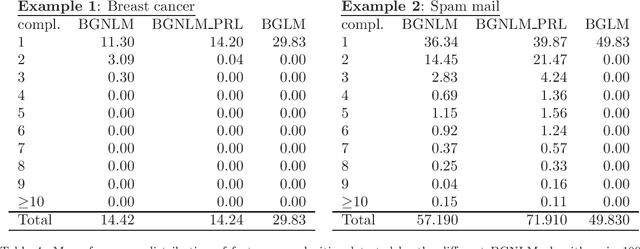
Regression models are used in a wide range of applications providing a powerful scientific tool for researchers from different fields. Linear models are often not sufficient to describe the complex relationship between input variables and a response. This relationship can be better described by non-linearities and complex functional interactions. Deep learning models have been extremely successful in terms of prediction although they are often difficult to specify and potentially suffer from overfitting. In this paper, we introduce a class of Bayesian generalized nonlinear regression models with a comprehensive non-linear feature space. Non-linear features are generated hierarchically, similarly to deep learning, but have additional flexibility on the possible types of features to be considered. This flexibility, combined with variable selection, allows us to find a small set of important features and thereby more interpretable models. A genetically modified Markov chain Monte Carlo algorithm is developed to make inference. Model averaging is also possible within our framework. In various applications, we illustrate how our approach is used to obtain meaningful non-linear models. Additionally, we compare its predictive performance with a number of machine learning algorithms.