Sparsifying Bayesian neural networks with latent binary variables and normalizing flows

Artificial neural networks (ANNs) are powerful machine learning methods used in many modern applications such as facial recognition, machine translation, and cancer diagnostics. A common issue with ANNs is that they usually have millions or billions of trainable parameters, and therefore tend to overfit to the training data. This is especially problematic in applications where it is important to have reliable uncertainty estimates. Bayesian neural networks (BNN) can improve on this, since they incorporate parameter uncertainty. In addition, latent binary Bayesian neural networks (LBBNN) also take into account structural uncertainty by allowing the weights to be turned on or off, enabling inference in the joint space of weights and structures. In this paper, we will consider two extensions to the LBBNN method: Firstly, by using the local reparametrization trick (LRT) to sample the hidden units directly, we get a more computationally efficient algorithm. More importantly, by using normalizing flows on the variational posterior distribution of the LBBNN parameters, the network learns a more flexible variational posterior distribution than the mean field Gaussian. Experimental results show that this improves predictive power compared to the LBBNN method, while also obtaining more sparse networks. We perform two simulation studies. In the first study, we consider variable selection in a logistic regression setting, where the more flexible variational distribution leads to improved results. In the second study, we compare predictive uncertainty based on data generated from two-dimensional Gaussian distributions. Here, we argue that our Bayesian methods lead to more realistic estimates of predictive uncertainty.

Variational Inference for Bayesian Neural Networks under Model and Parameter Uncertainty

Bayesian neural networks (BNNs) have recently regained a significant amount of attention in the deep learning community due to the development of scalable approximate Bayesian inference techniques. There are several advantages of using a Bayesian approach: Parameter and prediction uncertainties become easily available, facilitating rigorous statistical analysis. Furthermore, prior knowledge can be incorporated. However, so far, there have been no scalable techniques capable of combining both structural and parameter uncertainty. In this paper, we apply the concept of model uncertainty as a framework for structural learning in BNNs and hence make inference in the joint space of structures/models and parameters. Moreover, we suggest an adaptation of a scalable variational inference approach with reparametrization of marginal inclusion probabilities to incorporate the model space constraints. Experimental results on a range of benchmark datasets show that we obtain comparable accuracy results with the competing models, but based on methods that are much more sparse than ordinary BNNs.

Reversible Genetically Modified Mode Jumping MCMC

In this paper, we introduce a reversible version of a genetically modified mode jumping Markov chain Monte Carlo algorithm (GMJMCMC) for inference on posterior model probabilities in complex model spaces, where the number of explanatory variables is prohibitively large for classical Markov Chain Monte Carlo methods. Unlike the earlier proposed GMJMCMC algorithm, the introduced algorithm is a proper MCMC and its limiting distribution corresponds to the posterior marginal model probabilities in the explored model space under reasonable regularity conditions.

Reversible Genetically Modified ModeJumping MCMC

In this paper, we introduce a reversible version of a genetically modified mode jumping Markov chain Monte Carlo algorithm (GMJMCMC) for inference on posterior model probabilities in complex model spaces, where the number of explanatory variables is prohibitively large for classical Markov Chain Monte Carlo methods. Unlike the earlier proposed GMJMCMC algorithm, the introduced algorithm is a proper MCMC and its limiting distribution corresponds to the posterior marginal model probabilities in the explored model space under reasonable regularity conditions.

Rejoinder for the discussion of the paper "A novel algorithmic approach to Bayesian Logic Regression"

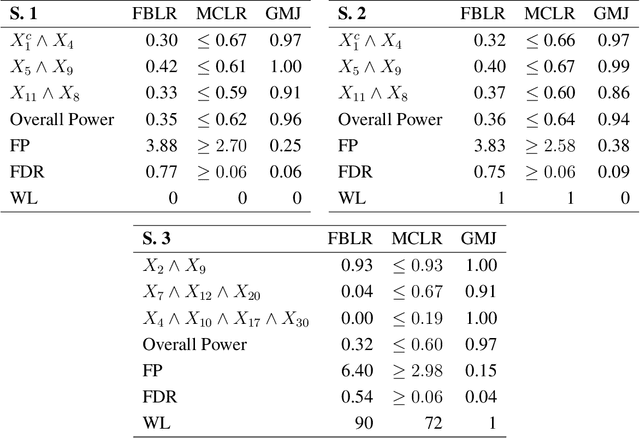
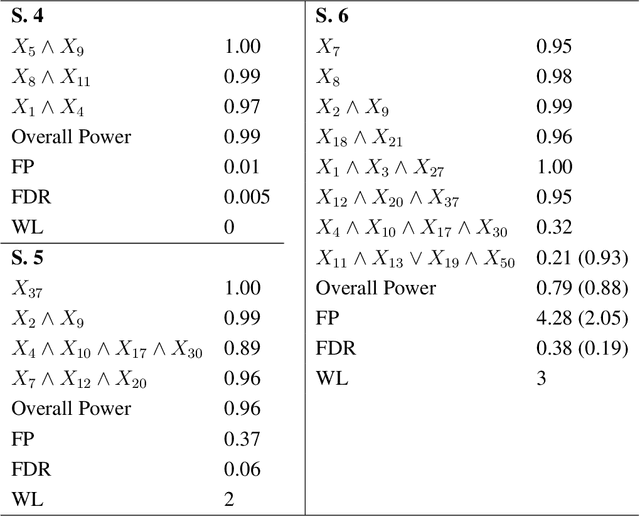
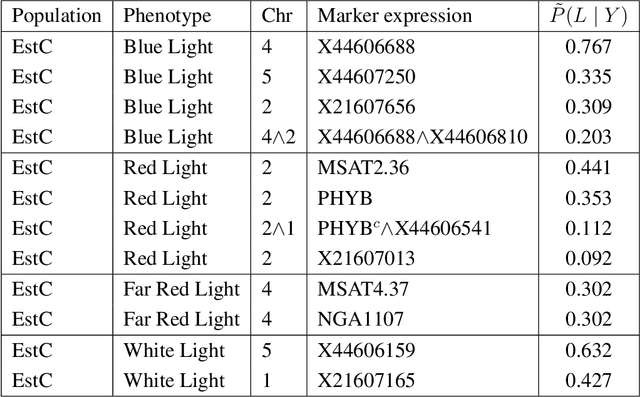
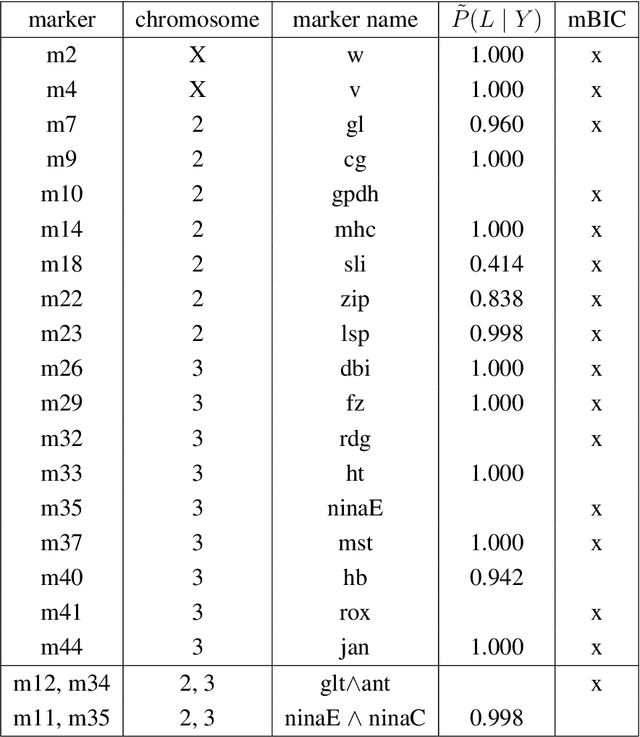
In this rejoinder we summarize the comments, questions and remarks on the paper "A novel algorithmic approach to Bayesian Logic Regression" from the discussants. We then respond to those comments, questions and remarks, provide several extensions of the original model and give a tutorial on our R-package EMJMCMC (http://aliaksah.github.io/EMJMCMC2016/)

Flexible Bayesian Nonlinear Model Configuration

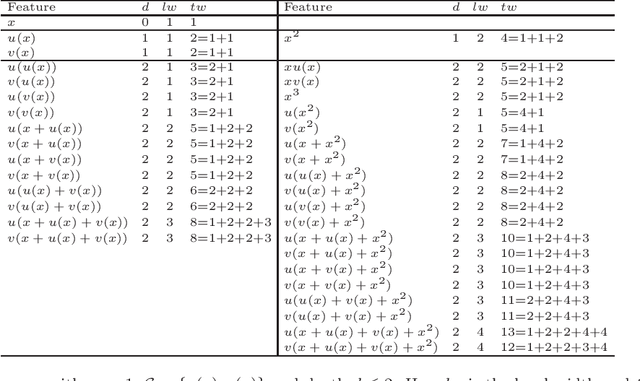
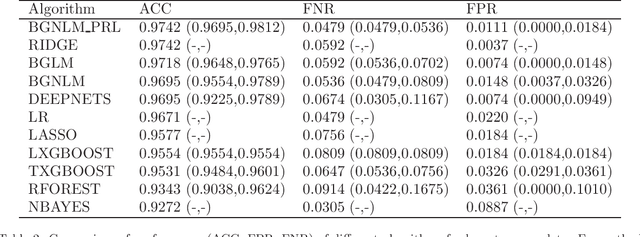
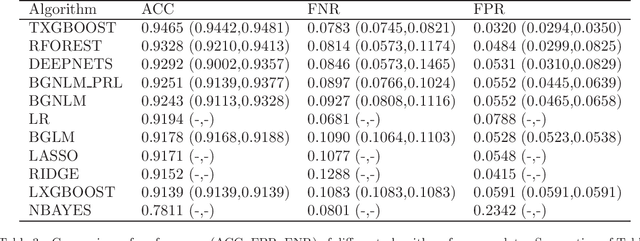
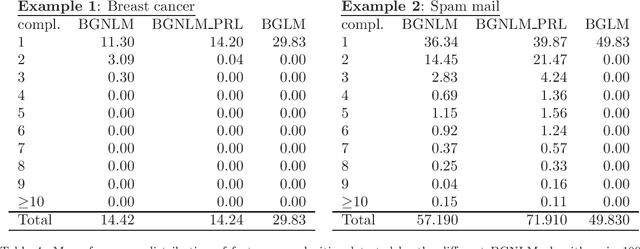
Regression models are used in a wide range of applications providing a powerful scientific tool for researchers from different fields. Linear models are often not sufficient to describe the complex relationship between input variables and a response. This relationship can be better described by non-linearities and complex functional interactions. Deep learning models have been extremely successful in terms of prediction although they are often difficult to specify and potentially suffer from overfitting. In this paper, we introduce a class of Bayesian generalized nonlinear regression models with a comprehensive non-linear feature space. Non-linear features are generated hierarchically, similarly to deep learning, but have additional flexibility on the possible types of features to be considered. This flexibility, combined with variable selection, allows us to find a small set of important features and thereby more interpretable models. A genetically modified Markov chain Monte Carlo algorithm is developed to make inference. Model averaging is also possible within our framework. In various applications, we illustrate how our approach is used to obtain meaningful non-linear models. Additionally, we compare its predictive performance with a number of machine learning algorithms.

Combining Model and Parameter Uncertainty in Bayesian Neural Networks

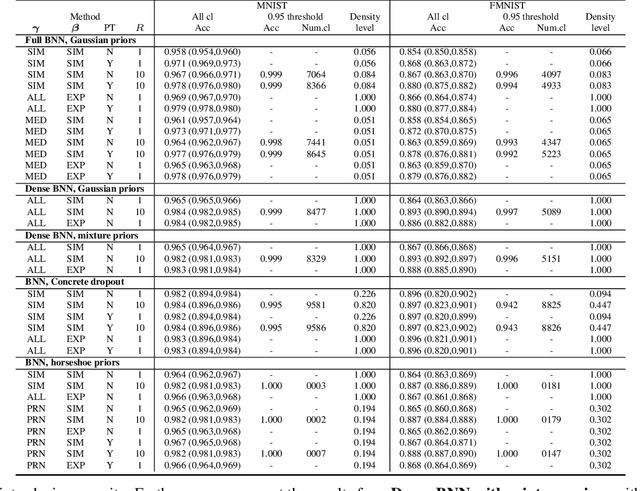
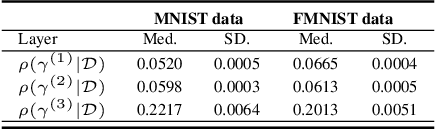
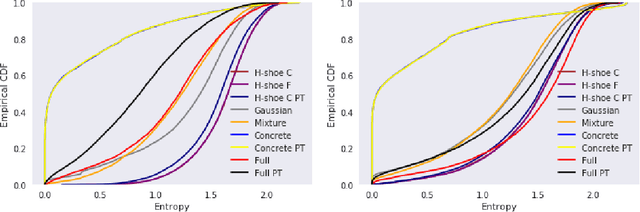
Bayesian neural networks (BNNs) have recently regained a significant amount of attention in the deep learning community due to the development of scalable approximate Bayesian inference techniques. There are several advantages of using Bayesian approach: Parameter and prediction uncertainty become easily available, facilitating rigid statistical analysis. Furthermore, prior knowledge can be incorporated. However so far there have been no scalable techniques capable of combining both model (structural) and parameter uncertainty. In this paper we introduce the concept of model uncertainty in BNNs and hence make inference in the joint space of models and parameters. Moreover, we suggest an adaptation of a scalable variational inference approach with reparametrization of marginal inclusion probabilities to incorporate the model space constraints. Finally, we show that incorporating model uncertainty via Bayesian model averaging and Bayesian model selection allows to drastically sparsify the structure of BNNs without significant loss of predictive power.