Combining Model and Parameter Uncertainty in Bayesian Neural Networks
Paper and Code
Mar 20, 2019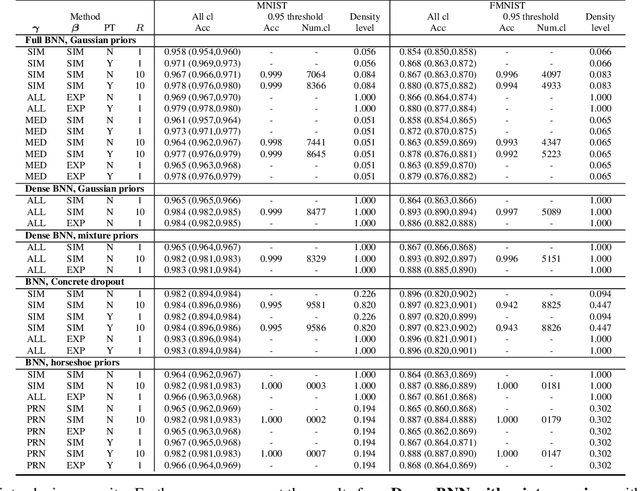

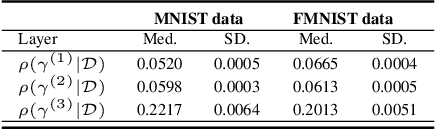
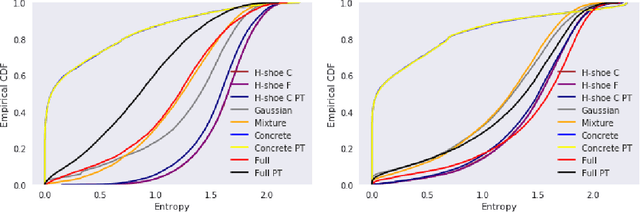
Bayesian neural networks (BNNs) have recently regained a significant amount of attention in the deep learning community due to the development of scalable approximate Bayesian inference techniques. There are several advantages of using Bayesian approach: Parameter and prediction uncertainty become easily available, facilitating rigid statistical analysis. Furthermore, prior knowledge can be incorporated. However so far there have been no scalable techniques capable of combining both model (structural) and parameter uncertainty. In this paper we introduce the concept of model uncertainty in BNNs and hence make inference in the joint space of models and parameters. Moreover, we suggest an adaptation of a scalable variational inference approach with reparametrization of marginal inclusion probabilities to incorporate the model space constraints. Finally, we show that incorporating model uncertainty via Bayesian model averaging and Bayesian model selection allows to drastically sparsify the structure of BNNs without significant loss of predictive power.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge