Alexandre d'Aspremont
FORMSpoT: A Decade of Tree-Level, Country-Scale Forest Monitoring
Dec 18, 2025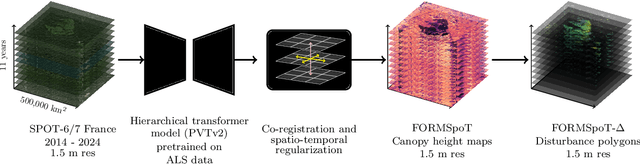
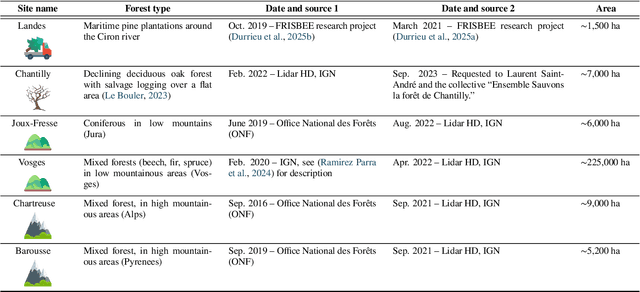
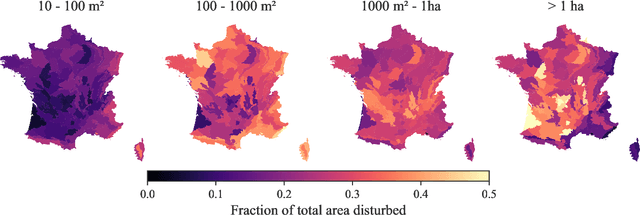
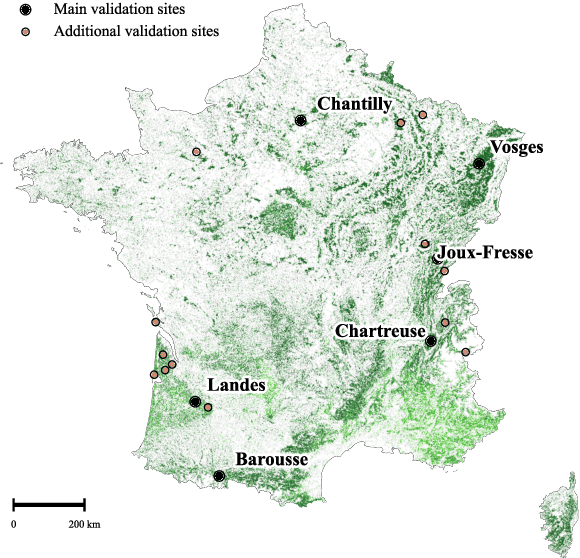
Abstract:The recent decline of the European forest carbon sink highlights the need for spatially explicit and frequently updated forest monitoring tools. Yet, existing satellite-based disturbance products remain too coarse to detect changes at the scale of individual trees, typically below 100 m$^{2}$. Here, we introduce FORMSpoT (Forest Mapping with SPOT Time series), a decade-long (2014-2024) nationwide mapping of forest canopy height at 1.5 m resolution, together with annual disturbance polygons (FORMSpoT-$Δ$) covering mainland France. Canopy heights were derived from annual SPOT-6/7 composites using a hierarchical transformer model (PVTv2) trained on high-resolution airborne laser scanning (ALS) data. To enable robust change detection across heterogeneous acquisitions, we developed a dedicated post-processing pipeline combining co-registration and spatio-temporal total variation denoising. Validation against ALS revisits across 19 sites and 5,087 National Forest Inventory plots shows that FORMSpoT-$Δ$ substantially outperforms existing disturbance products. In mountainous forests, where disturbances are small and spatially fragmented, FORMSpoT-$Δ$ achieves an F1-score of 0.44, representing an order of magnitude higher than existing benchmarks. By enabling tree-level monitoring of forest dynamics at national scale, FORMSpoT-$Δ$ provides a unique tool to analyze management practices, detect early signals of forest decline, and better quantify carbon losses from subtle disturbances such as thinning or selective logging. These results underscore the critical importance of sustaining very high-resolution satellite missions like SPOT and open-data initiatives such as DINAMIS for monitoring forests under climate change.
DUNIA: Pixel-Sized Embeddings via Cross-Modal Alignment for Earth Observation Applications
Feb 24, 2025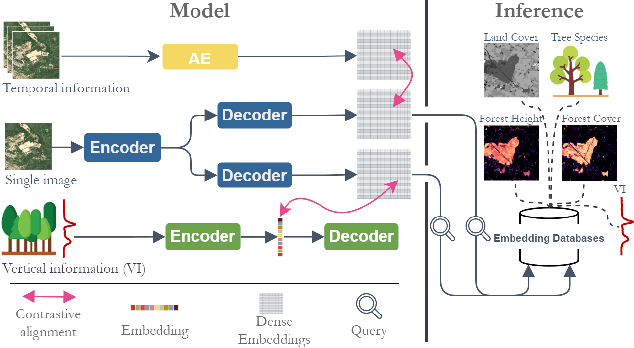
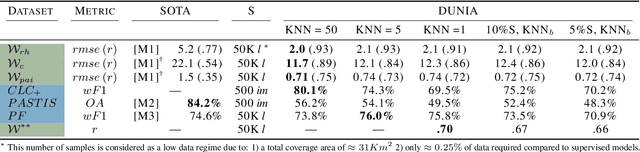
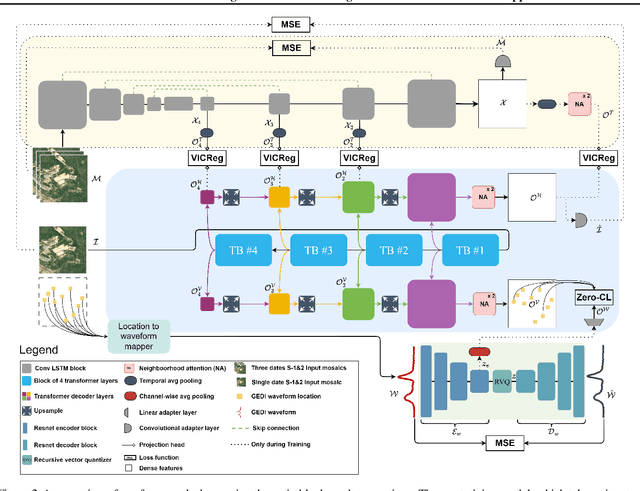

Abstract:Significant efforts have been directed towards adapting self-supervised multimodal learning for Earth observation applications. However, existing methods produce coarse patch-sized embeddings, limiting their effectiveness and integration with other modalities like LiDAR. To close this gap, we present DUNIA, an approach to learn pixel-sized embeddings through cross-modal alignment between images and full-waveform LiDAR data. As the model is trained in a contrastive manner, the embeddings can be directly leveraged in the context of a variety of environmental monitoring tasks in a zero-shot setting. In our experiments, we demonstrate the effectiveness of the embeddings for seven such tasks (canopy height mapping, fractional canopy cover, land cover mapping, tree species identification, plant area index, crop type classification, and per-pixel waveform-based vertical structure mapping). The results show that the embeddings, along with zero-shot classifiers, often outperform specialized supervised models, even in low data regimes. In the fine-tuning setting, we show strong low-shot capabilities with performances near or better than state-of-the-art on five out of six tasks.
Open-Canopy: A Country-Scale Benchmark for Canopy Height Estimation at Very High Resolution
Jul 12, 2024



Abstract:Estimating canopy height and canopy height change at meter resolution from satellite imagery has numerous applications, such as monitoring forest health, logging activities, wood resources, and carbon stocks. However, many existing forest datasets are based on commercial or closed data sources, restricting the reproducibility and evaluation of new approaches. To address this gap, we introduce Open-Canopy, the first open-access and country-scale benchmark for very high resolution (1.5 m) canopy height estimation. Covering more than 87,000 km$^2$ across France, Open-Canopy combines SPOT satellite imagery with high resolution aerial LiDAR data. We also propose Open-Canopy-$\Delta$, the first benchmark for canopy height change detection between two images taken at different years, a particularly challenging task even for recent models. To establish a robust foundation for these benchmarks, we evaluate a comprehensive list of state-of-the-art computer vision models for canopy height estimation. The dataset and associated codes can be accessed at https://github.com/fajwel/Open-Canopy.
An Oblivious Stochastic Composite Optimization Algorithm for Eigenvalue Optimization Problems
Jun 30, 2023Abstract:In this work, we revisit the problem of solving large-scale semidefinite programs using randomized first-order methods and stochastic smoothing. We introduce two oblivious stochastic mirror descent algorithms based on a complementary composite setting. One algorithm is designed for non-smooth objectives, while an accelerated version is tailored for smooth objectives. Remarkably, both algorithms work without prior knowledge of the Lipschitz constant or smoothness of the objective function. For the non-smooth case with $\mathcal{M}-$bounded oracles, we prove a convergence rate of $ O( {\mathcal{M}}/{\sqrt{T}} ) $. For the $L$-smooth case with a feasible set bounded by $D$, we derive a convergence rate of $ O( {L^2 D^2}/{(T^{2}\sqrt{T})} + {(D_0^2+\sigma^2)}/{\sqrt{T}} )$, where $D_0$ is the starting distance to an optimal solution, and $ \sigma^2$ is the stochastic oracle variance. These rates had only been obtained so far by either assuming prior knowledge of the Lipschitz constant or the starting distance to an optimal solution. We further show how to extend our framework to relative scale and demonstrate the efficiency and robustness of our methods on large scale semidefinite programs.
Vision Transformers, a new approach for high-resolution and large-scale mapping of canopy heights
Apr 22, 2023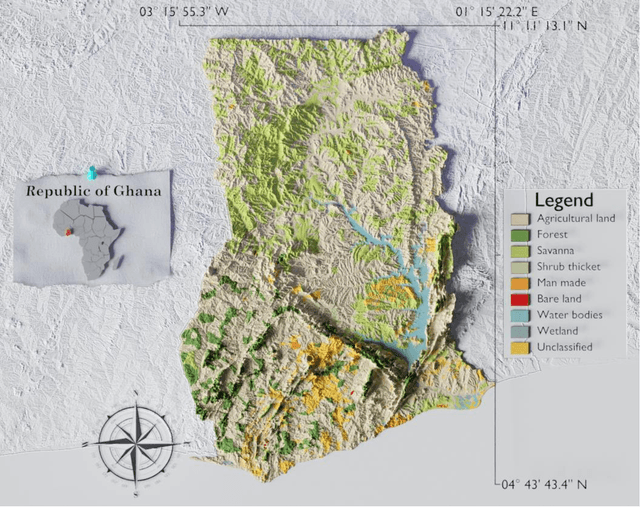

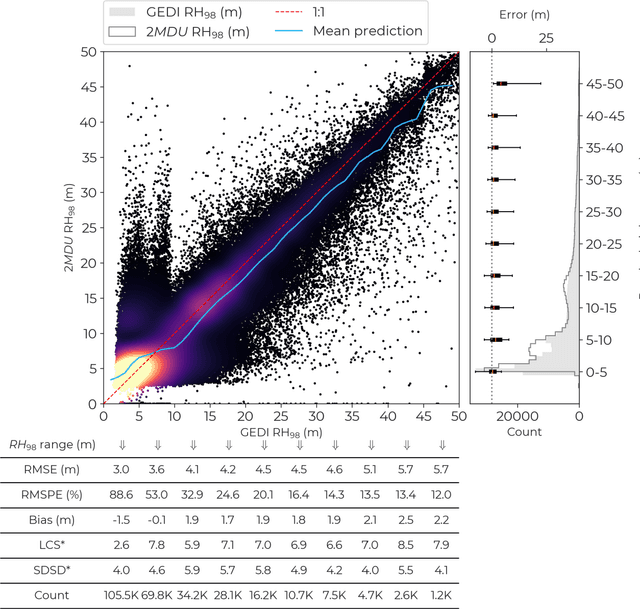
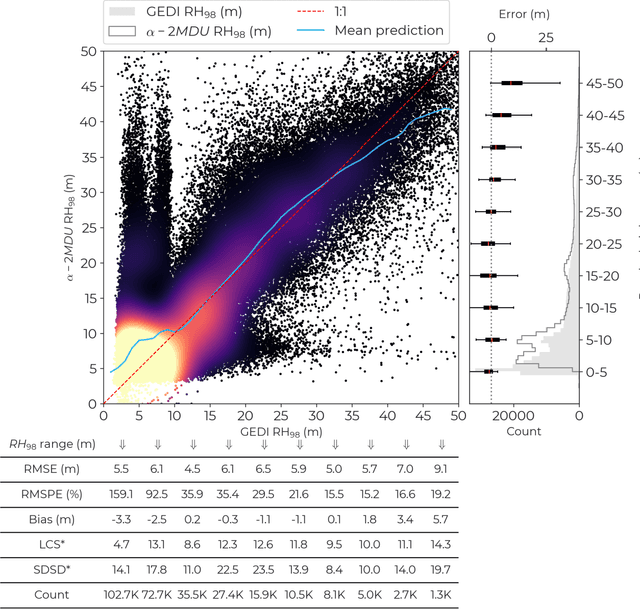
Abstract:Accurate and timely monitoring of forest canopy heights is critical for assessing forest dynamics, biodiversity, carbon sequestration as well as forest degradation and deforestation. Recent advances in deep learning techniques, coupled with the vast amount of spaceborne remote sensing data offer an unprecedented opportunity to map canopy height at high spatial and temporal resolutions. Current techniques for wall-to-wall canopy height mapping correlate remotely sensed 2D information from optical and radar sensors to the vertical structure of trees using LiDAR measurements. While studies using deep learning algorithms have shown promising performances for the accurate mapping of canopy heights, they have limitations due to the type of architectures and loss functions employed. Moreover, mapping canopy heights over tropical forests remains poorly studied, and the accurate height estimation of tall canopies is a challenge due to signal saturation from optical and radar sensors, persistent cloud covers and sometimes the limited penetration capabilities of LiDARs. Here, we map heights at 10 m resolution across the diverse landscape of Ghana with a new vision transformer (ViT) model optimized concurrently with a classification (discrete) and a regression (continuous) loss function. This model achieves better accuracy than previously used convolutional based approaches (ConvNets) optimized with only a continuous loss function. The ViT model results show that our proposed discrete/continuous loss significantly increases the sensitivity for very tall trees (i.e., > 35m), for which other approaches show saturation effects. The height maps generated by the ViT also have better ground sampling distance and better sensitivity to sparse vegetation in comparison to a convolutional model. Our ViT model has a RMSE of 3.12m in comparison to a reference dataset while the ConvNet model has a RMSE of 4.3m.
Detecting Methane Plumes using PRISMA: Deep Learning Model and Data Augmentation
Nov 17, 2022



Abstract:The new generation of hyperspectral imagers, such as PRISMA, has improved significantly our detection capability of methane (CH4) plumes from space at high spatial resolution (30m). We present here a complete framework to identify CH4 plumes using images from the PRISMA satellite mission and a deep learning model able to detect plumes over large areas. To compensate for the relative scarcity of PRISMA images, we trained our model by transposing high resolution plumes from Sentinel-2 to PRISMA. Our methodology thus avoids computationally expensive synthetic plume generation from Large Eddy Simulations by generating a broad and realistic training database, and paves the way for large-scale detection of methane plumes using future hyperspectral sensors (EnMAP, EMIT, CarbonMapper).
Optimal Algorithms for Stochastic Complementary Composite Minimization
Nov 03, 2022Abstract:Inspired by regularization techniques in statistics and machine learning, we study complementary composite minimization in the stochastic setting. This problem corresponds to the minimization of the sum of a (weakly) smooth function endowed with a stochastic first-order oracle, and a structured uniformly convex (possibly nonsmooth and non-Lipschitz) regularization term. Despite intensive work on closely related settings, prior to our work no complexity bounds for this problem were known. We close this gap by providing novel excess risk bounds, both in expectation and with high probability. Our algorithms are nearly optimal, which we prove via novel lower complexity bounds for this class of problems. We conclude by providing numerical results comparing our methods to the state of the art.
Linear Bandits on Uniformly Convex Sets
Mar 10, 2021Abstract:Linear bandit algorithms yield $\tilde{\mathcal{O}}(n\sqrt{T})$ pseudo-regret bounds on compact convex action sets $\mathcal{K}\subset\mathbb{R}^n$ and two types of structural assumptions lead to better pseudo-regret bounds. When $\mathcal{K}$ is the simplex or an $\ell_p$ ball with $p\in]1,2]$, there exist bandits algorithms with $\tilde{\mathcal{O}}(\sqrt{nT})$ pseudo-regret bounds. Here, we derive bandit algorithms for some strongly convex sets beyond $\ell_p$ balls that enjoy pseudo-regret bounds of $\tilde{\mathcal{O}}(\sqrt{nT})$, which answers an open question from [BCB12, \S 5.5.]. Interestingly, when the action set is uniformly convex but not necessarily strongly convex, we obtain pseudo-regret bounds with a dimension dependency smaller than $\mathcal{O}(\sqrt{n})$. However, this comes at the expense of asymptotic rates in $T$ varying between $\tilde{\mathcal{O}}(\sqrt{T})$ and $\tilde{\mathcal{O}}(T)$.
Local and Global Uniform Convexity Conditions
Feb 18, 2021Abstract:We review various characterizations of uniform convexity and smoothness on norm balls in finite-dimensional spaces and connect results stemming from the geometry of Banach spaces with \textit{scaling inequalities} used in analysing the convergence of optimization methods. In particular, we establish local versions of these conditions to provide sharper insights on a recent body of complexity results in learning theory, online learning, or offline optimization, which rely on the strong convexity of the feasible set. While they have a significant impact on complexity, these strong convexity or uniform convexity properties of feasible sets are not exploited as thoroughly as their functional counterparts, and this work is an effort to correct this imbalance. We conclude with some practical examples in optimization and machine learning where leveraging these conditions and localized assumptions lead to new complexity results.
Acceleration Methods
Jan 23, 2021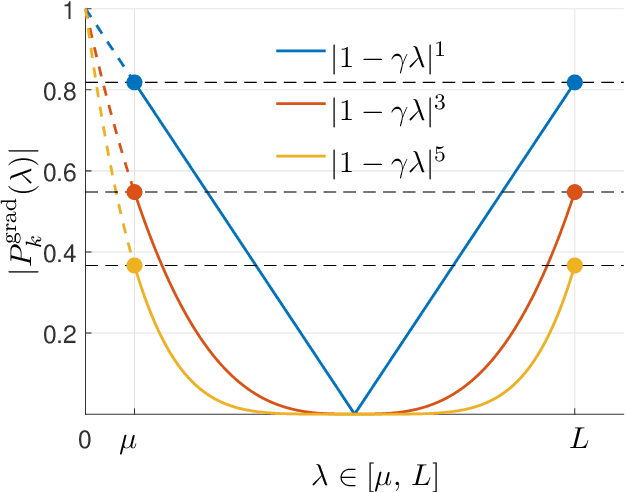
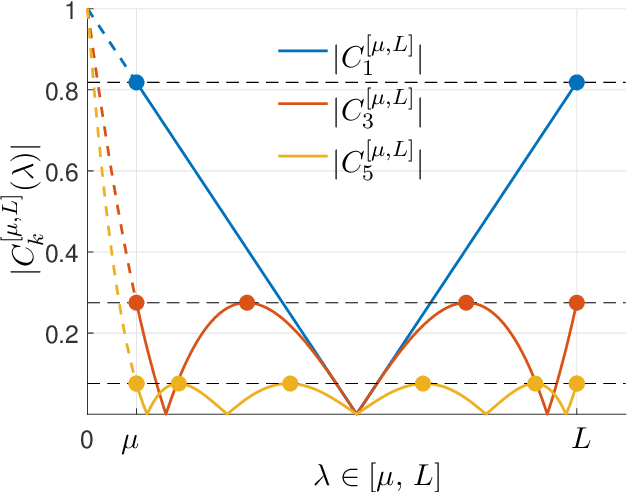
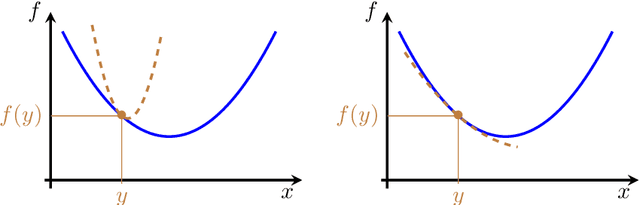
Abstract:This monograph covers some recent advances on a range of acceleration techniques frequently used in convex optimization. We first use quadratic optimization problems to introduce two key families of methods, momentum and nested optimization schemes, which coincide in the quadratic case to form the Chebyshev method whose complexity is analyzed using Chebyshev polynomials. We discuss momentum methods in detail, starting with the seminal work of Nesterov (1983) and structure convergence proofs using a few master templates, such as that of \emph{optimized gradient methods} which have the key benefit of showing how momentum methods maximize convergence rates. We further cover proximal acceleration techniques, at the heart of the \emph{Catalyst} and \emph{Accelerated Hybrid Proximal Extragradient} frameworks, using similar algorithmic patterns. Common acceleration techniques directly rely on the knowledge of some regularity parameters of the problem at hand, and we conclude by discussing \emph{restart} schemes, a set of simple techniques to reach nearly optimal convergence rates while adapting to unobserved regularity parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge