Fajwel Fogel
SERA-H: Beyond Native Sentinel Spatial Limits for High-Resolution Canopy Height Mapping
Dec 19, 2025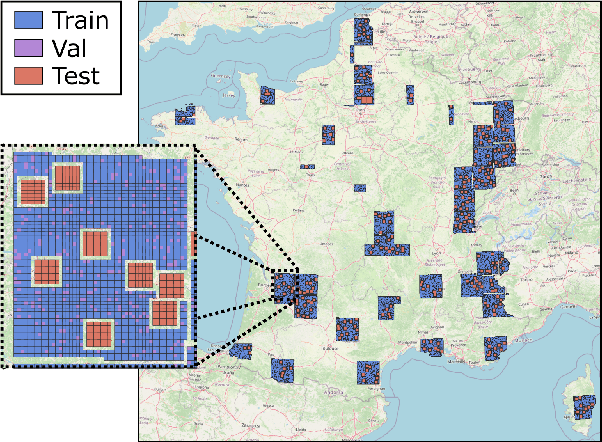
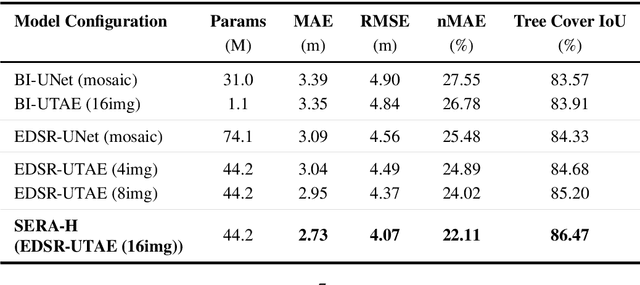
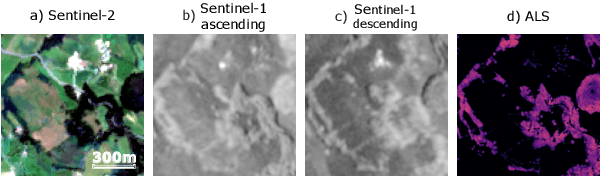
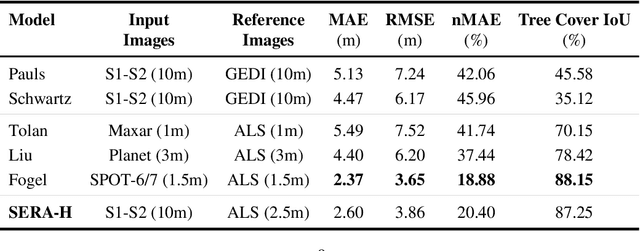
Abstract:High-resolution mapping of canopy height is essential for forest management and biodiversity monitoring. Although recent studies have led to the advent of deep learning methods using satellite imagery to predict height maps, these approaches often face a trade-off between data accessibility and spatial resolution. To overcome these limitations, we present SERA-H, an end-to-end model combining a super-resolution module (EDSR) and temporal attention encoding (UTAE). Trained under the supervision of high-density LiDAR data (ALS), our model generates 2.5 m resolution height maps from freely available Sentinel-1 and Sentinel-2 (10 m) time series data. Evaluated on an open-source benchmark dataset in France, SERA-H, with a MAE of 2.6 m and a coefficient of determination of 0.82, not only outperforms standard Sentinel-1/2 baselines but also achieves performance comparable to or better than methods relying on commercial very high-resolution imagery (SPOT-6/7, PlanetScope, Maxar). These results demonstrate that combining high-resolution supervision with the spatiotemporal information embedded in time series enables the reconstruction of details beyond the input sensors' native resolution. SERA-H opens the possibility of freely mapping forests with high revisit frequency, achieving accuracy comparable to that of costly commercial imagery. The source code is available at https://github.com/ThomasBoudras/SERA-H#
FORMSpoT: A Decade of Tree-Level, Country-Scale Forest Monitoring
Dec 18, 2025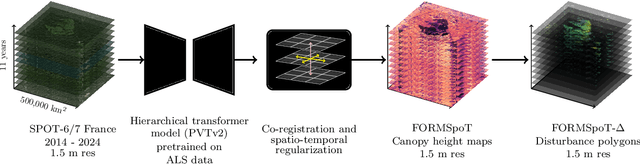
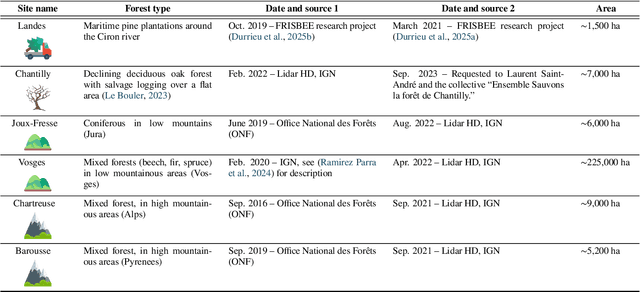
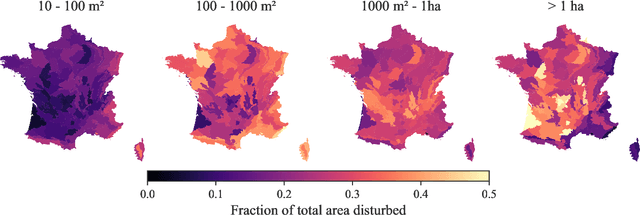
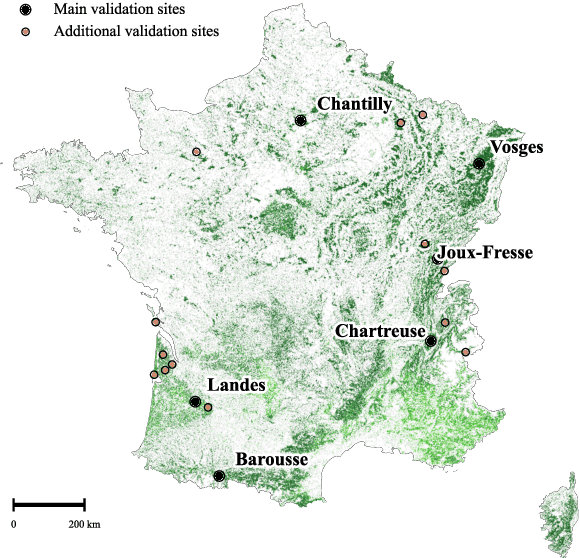
Abstract:The recent decline of the European forest carbon sink highlights the need for spatially explicit and frequently updated forest monitoring tools. Yet, existing satellite-based disturbance products remain too coarse to detect changes at the scale of individual trees, typically below 100 m$^{2}$. Here, we introduce FORMSpoT (Forest Mapping with SPOT Time series), a decade-long (2014-2024) nationwide mapping of forest canopy height at 1.5 m resolution, together with annual disturbance polygons (FORMSpoT-$Δ$) covering mainland France. Canopy heights were derived from annual SPOT-6/7 composites using a hierarchical transformer model (PVTv2) trained on high-resolution airborne laser scanning (ALS) data. To enable robust change detection across heterogeneous acquisitions, we developed a dedicated post-processing pipeline combining co-registration and spatio-temporal total variation denoising. Validation against ALS revisits across 19 sites and 5,087 National Forest Inventory plots shows that FORMSpoT-$Δ$ substantially outperforms existing disturbance products. In mountainous forests, where disturbances are small and spatially fragmented, FORMSpoT-$Δ$ achieves an F1-score of 0.44, representing an order of magnitude higher than existing benchmarks. By enabling tree-level monitoring of forest dynamics at national scale, FORMSpoT-$Δ$ provides a unique tool to analyze management practices, detect early signals of forest decline, and better quantify carbon losses from subtle disturbances such as thinning or selective logging. These results underscore the critical importance of sustaining very high-resolution satellite missions like SPOT and open-data initiatives such as DINAMIS for monitoring forests under climate change.
Open-Canopy: A Country-Scale Benchmark for Canopy Height Estimation at Very High Resolution
Jul 12, 2024



Abstract:Estimating canopy height and canopy height change at meter resolution from satellite imagery has numerous applications, such as monitoring forest health, logging activities, wood resources, and carbon stocks. However, many existing forest datasets are based on commercial or closed data sources, restricting the reproducibility and evaluation of new approaches. To address this gap, we introduce Open-Canopy, the first open-access and country-scale benchmark for very high resolution (1.5 m) canopy height estimation. Covering more than 87,000 km$^2$ across France, Open-Canopy combines SPOT satellite imagery with high resolution aerial LiDAR data. We also propose Open-Canopy-$\Delta$, the first benchmark for canopy height change detection between two images taken at different years, a particularly challenging task even for recent models. To establish a robust foundation for these benchmarks, we evaluate a comprehensive list of state-of-the-art computer vision models for canopy height estimation. The dataset and associated codes can be accessed at https://github.com/fajwel/Open-Canopy.
Learning with Clustering Structure
Sep 19, 2016



Abstract:We study supervised learning problems using clustering constraints to impose structure on either features or samples, seeking to help both prediction and interpretation. The problem of clustering features arises naturally in text classification for instance, to reduce dimensionality by grouping words together and identify synonyms. The sample clustering problem on the other hand, applies to multiclass problems where we are allowed to make multiple predictions and the performance of the best answer is recorded. We derive a unified optimization formulation highlighting the common structure of these problems and produce algorithms whose core iteration complexity amounts to a k-means clustering step, which can be approximated efficiently. We extend these results to combine sparsity and clustering constraints, and develop a new projection algorithm on the set of clustered sparse vectors. We prove convergence of our algorithms on random instances, based on a union of subspaces interpretation of the clustering structure. Finally, we test the robustness of our methods on artificial data sets as well as real data extracted from movie reviews.
Spectral Ranking using Seriation
Mar 10, 2016


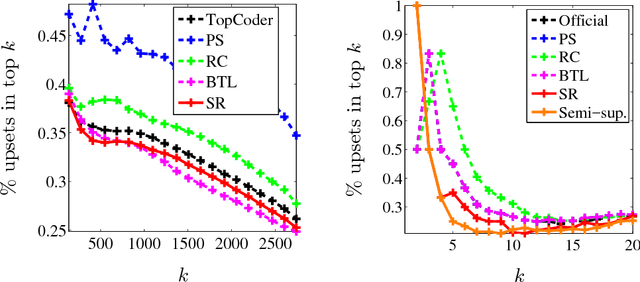
Abstract:We describe a seriation algorithm for ranking a set of items given pairwise comparisons between these items. Intuitively, the algorithm assigns similar rankings to items that compare similarly with all others. It does so by constructing a similarity matrix from pairwise comparisons, using seriation methods to reorder this matrix and construct a ranking. We first show that this spectral seriation algorithm recovers the true ranking when all pairwise comparisons are observed and consistent with a total order. We then show that ranking reconstruction is still exact when some pairwise comparisons are corrupted or missing, and that seriation based spectral ranking is more robust to noise than classical scoring methods. Finally, we bound the ranking error when only a random subset of the comparions are observed. An additional benefit of the seriation formulation is that it allows us to solve semi-supervised ranking problems. Experiments on both synthetic and real datasets demonstrate that seriation based spectral ranking achieves competitive and in some cases superior performance compared to classical ranking methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge