Reducing the Cost of Quantum Chemical Data By Backpropagating Through Density Functional Theory

Density Functional Theory (DFT) accurately predicts the quantum chemical properties of molecules, but scales as $O(N_{\text{electrons}}^3)$. Sch\"utt et al. (2019) successfully approximate DFT 1000x faster with Neural Networks (NN). Arguably, the biggest problem one faces when scaling to larger molecules is the cost of DFT labels. For example, it took years to create the PCQ dataset (Nakata & Shimazaki, 2017) on which subsequent NNs are trained within a week. DFT labels molecules by minimizing energy $E(\cdot )$ as a "loss function." We bypass dataset creation by directly training NNs with $E(\cdot )$ as a loss function. For comparison, Sch\"utt et al. (2019) spent 626 hours creating a dataset on which they trained their NN for 160h, for a total of 786h; our method achieves comparable performance within 31h.

Generating QM1B with PySCF$_{\text{IPU}}$

The emergence of foundation models in Computer Vision and Natural Language Processing have resulted in immense progress on downstream tasks. This progress was enabled by datasets with billions of training examples. Similar benefits are yet to be unlocked for quantum chemistry, where the potential of deep learning is constrained by comparatively small datasets with 100k to 20M training examples. These datasets are limited in size because the labels are computed using the accurate (but computationally demanding) predictions of Density Functional Theory (DFT). Notably, prior DFT datasets were created using CPU supercomputers without leveraging hardware acceleration. In this paper, we take a first step towards utilising hardware accelerators by introducing the data generator PySCF$_{\text{IPU}}$ using Intelligence Processing Units (IPUs). This allowed us to create the dataset QM1B with one billion training examples containing 9-11 heavy atoms. We demonstrate that a simple baseline neural network (SchNet 9M) improves its performance by simply increasing the amount of training data without additional inductive biases. To encourage future researchers to use QM1B responsibly, we highlight several limitations of QM1B and emphasise the low-resolution of our DFT options, which also serves as motivation for even larger, more accurate datasets. Code and dataset are available on Github: http://github.com/graphcore-research/pyscf-ipu

One Reflection Suffice

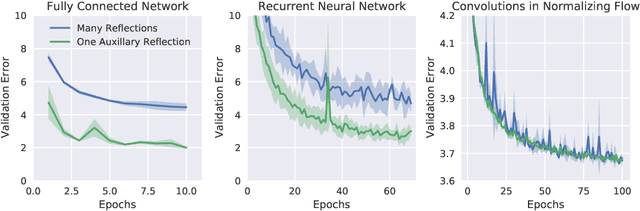
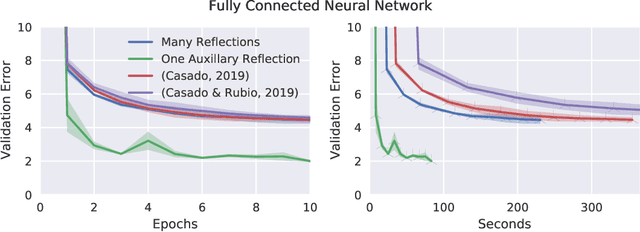
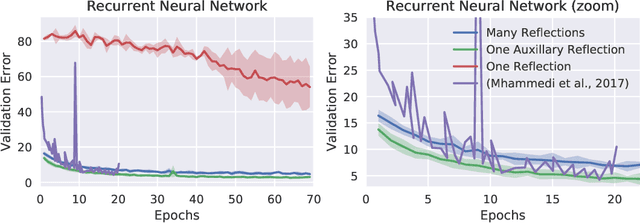
Orthogonal weight matrices are used in many areas of deep learning. Much previous work attempt to alleviate the additional computational resources it requires to constrain weight matrices to be orthogonal. One popular approach utilizes *many* Householder reflections. The only practical drawback is that many reflections cause low GPU utilization. We mitigate this final drawback by proving that *one* reflection is sufficient, if the reflection is computed by an auxiliary neural network.

Fast Fréchet Inception Distance

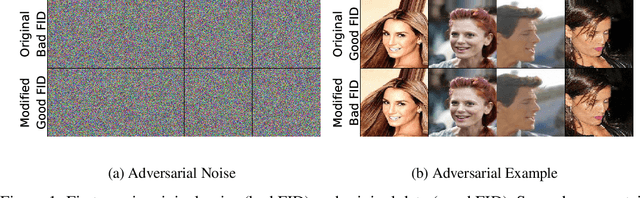
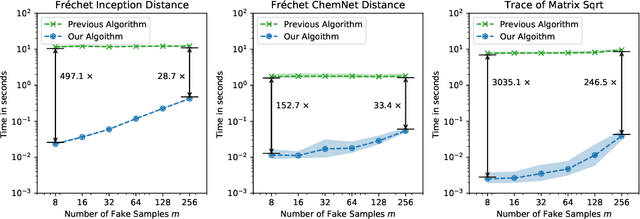
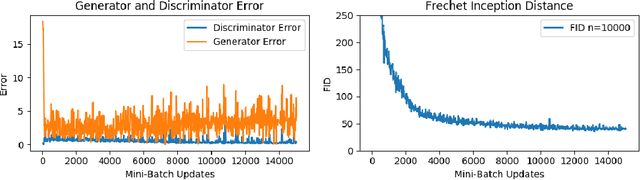
The Fr\'echet Inception Distance (FID) has been used to evaluate thousands of generative models. We present a novel algorithm, FastFID, which allows fast computation and backpropagation for FID. FastFID can efficiently (1) evaluate generative model *during* training and (2) construct adversarial examples for FID.

What if Neural Networks had SVDs?

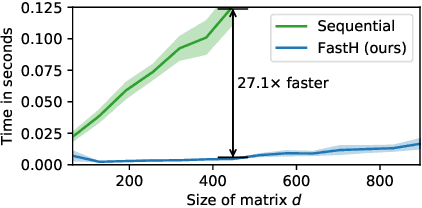
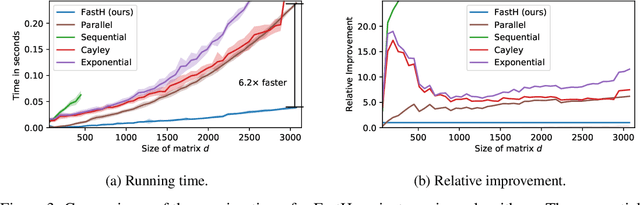
Various Neural Networks employ time-consuming matrix operations like matrix inversion. Many such matrix operations are faster to compute given the Singular Value Decomposition (SVD). Previous work allows using the SVD in Neural Networks without computing it. In theory, the techniques can speed up matrix operations, however, in practice, they are not fast enough. We present an algorithm that is fast enough to speed up several matrix operations. The algorithm increases the degree of parallelism of an underlying matrix multiplication $H\cdot X$ where $H$ is an orthogonal matrix represented by a product of Householder matrices. Code is available at www.github.com/AlexanderMath/fasth .

Margin-Based Generalization Lower Bounds for Boosted Classifiers

Boosting is one of the most successful ideas in machine learning. The most well-accepted explanations for the low generalization error of boosting algorithms such as AdaBoost stem from margin theory. The study of margins in the context of boosting algorithms was initiated by Schapire, Freund, Bartlett and Lee (1998) and has inspired numerous boosting algorithms and generalization bounds. To date, the strongest known generalization (upper bound) is the $k$th margin bound of Gao and Zhou (2013). Despite the numerous generalization upper bounds that have been proved over the last two decades, nothing is known about the tightness of these bounds. In this paper, we give the first margin-based lower bounds on the generalization error of boosted classifiers. Our lower bounds nearly match the $k$th margin bound and thus almost settle the generalization performance of boosted classifiers in terms of margins.

Optimal Minimal Margin Maximization with Boosting

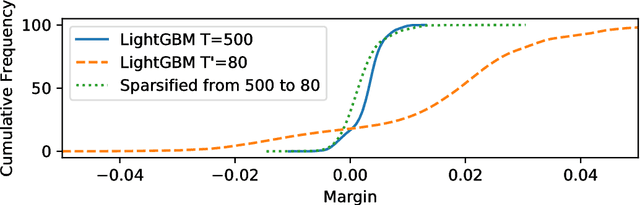
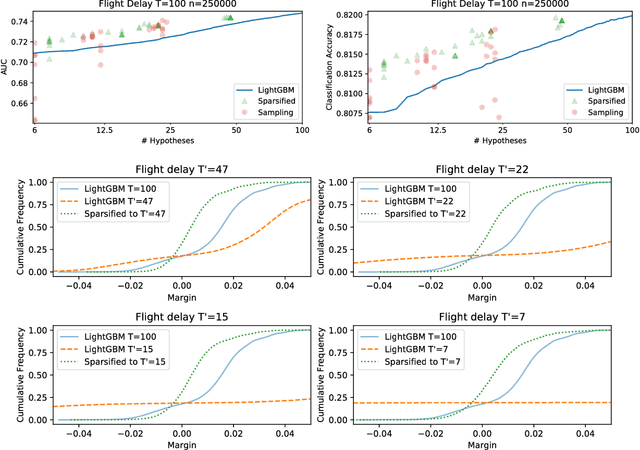
Boosting algorithms produce a classifier by iteratively combining base hypotheses. It has been observed experimentally that the generalization error keeps improving even after achieving zero training error. One popular explanation attributes this to improvements in margins. A common goal in a long line of research, is to maximize the smallest margin using as few base hypotheses as possible, culminating with the AdaBoostV algorithm by (R{\"a}tsch and Warmuth [JMLR'04]). The AdaBoostV algorithm was later conjectured to yield an optimal trade-off between number of hypotheses trained and the minimal margin over all training points (Nie et al. [JMLR'13]). Our main contribution is a new algorithm refuting this conjecture. Furthermore, we prove a lower bound which implies that our new algorithm is optimal.

Fast Exact k-Means, k-Medians and Bregman Divergence Clustering in 1D

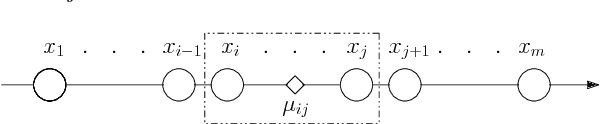
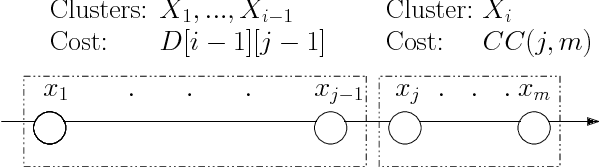
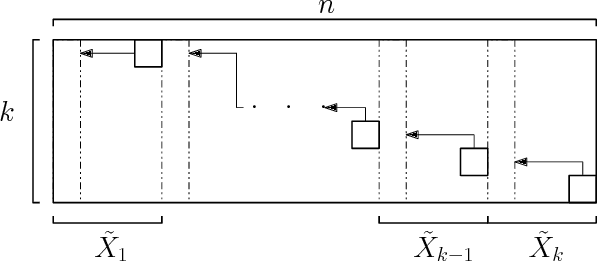
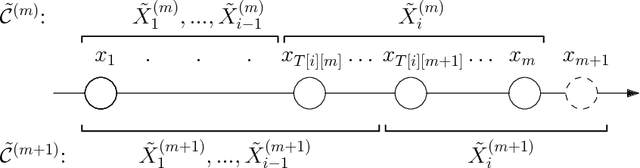
The $k$-Means clustering problem on $n$ points is NP-Hard for any dimension $d\ge 2$, however, for the 1D case there exists exact polynomial time algorithms. Previous literature reported an $O(kn^2)$ time dynamic programming algorithm that uses $O(kn)$ space. It turns out that the problem has been considered under a different name more than twenty years ago. We present all the existing work that had been overlooked and compare the various solutions theoretically. Moreover, we show how to reduce the space usage for some of them, as well as generalize them to data structures that can quickly report an optimal $k$-Means clustering for any $k$. Finally we also generalize all the algorithms to work for the absolute distance and to work for any Bregman Divergence. We complement our theoretical contributions by experiments that compare the practical performance of the various algorithms.