Mingzhou Song
Fast Exact k-Means, k-Medians and Bregman Divergence Clustering in 1D
Apr 25, 2018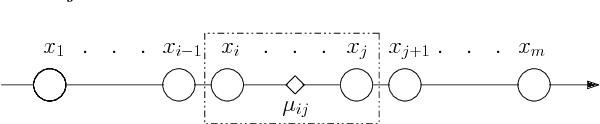
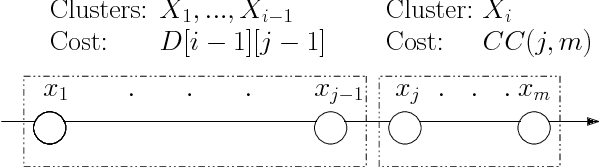
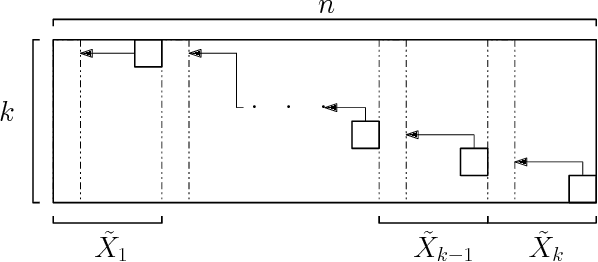
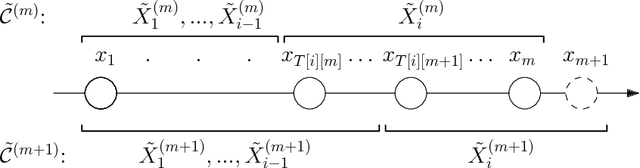
Abstract:The $k$-Means clustering problem on $n$ points is NP-Hard for any dimension $d\ge 2$, however, for the 1D case there exists exact polynomial time algorithms. Previous literature reported an $O(kn^2)$ time dynamic programming algorithm that uses $O(kn)$ space. It turns out that the problem has been considered under a different name more than twenty years ago. We present all the existing work that had been overlooked and compare the various solutions theoretically. Moreover, we show how to reduce the space usage for some of them, as well as generalize them to data structures that can quickly report an optimal $k$-Means clustering for any $k$. Finally we also generalize all the algorithms to work for the absolute distance and to work for any Bregman Divergence. We complement our theoretical contributions by experiments that compare the practical performance of the various algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge