An Exponential Separation Between Quantum and Quantum-Inspired Classical Algorithms for Machine Learning

Achieving a provable exponential quantum speedup for an important machine learning task has been a central research goal since the seminal HHL quantum algorithm for solving linear systems and the subsequent quantum recommender systems algorithm by Kerenidis and Prakash. These algorithms were initially believed to be strong candidates for exponential speedups, but a lower bound ruling out similar classical improvements remained absent. In breakthrough work by Tang, it was demonstrated that this lack of progress in classical lower bounds was for good reasons. Concretely, she gave a classical counterpart of the quantum recommender systems algorithm, reducing the quantum advantage to a mere polynomial. Her approach is quite general and was named quantum-inspired classical algorithms. Since then, almost all the initially exponential quantum machine learning speedups have been reduced to polynomial via new quantum-inspired classical algorithms. From the current state-of-affairs, it is unclear whether we can hope for exponential quantum speedups for any natural machine learning task. In this work, we present the first such provable exponential separation between quantum and quantum-inspired classical algorithms. We prove the separation for the basic problem of solving a linear system when the input matrix is well-conditioned and has sparse rows and columns.

Compression Implies Generalization

Explaining the surprising generalization performance of deep neural networks is an active and important line of research in theoretical machine learning. Influential work by Arora et al. (ICML'18) showed that, noise stability properties of deep nets occurring in practice can be used to provably compress model representations. They then argued that the small representations of compressed networks imply good generalization performance albeit only of the compressed nets. Extending their compression framework to yield generalization bounds for the original uncompressed networks remains elusive. Our main contribution is the establishment of a compression-based framework for proving generalization bounds. The framework is simple and powerful enough to extend the generalization bounds by Arora et al. to also hold for the original network. To demonstrate the flexibility of the framework, we also show that it allows us to give simple proofs of the strongest known generalization bounds for other popular machine learning models, namely Support Vector Machines and Boosting.

Learning to Detect Fortified Areas

High resolution data models like grid terrain models made from LiDAR data are a prerequisite for modern day Geographic Information Systems applications. Besides providing the foundation for the very accurate digital terrain models, LiDAR data is also extensively used to classify which parts of the considered surface comprise relevant elements like water, buildings and vegetation. In this paper we consider the problem of classifying which areas of a given surface are fortified by for instance, roads, sidewalks, parking spaces, paved driveways and terraces. We consider using LiDAR data and orthophotos, combined and alone, to show how well the modern machine learning algorithms Gradient Boosted Trees and Convolutional Neural Networks are able to detect fortified areas on large real world data. The LiDAR data features, in particular the intensity feature that measures the signal strength of the return, that we consider in this project are heavily dependent on the actual LiDAR sensor that made the measurement. This is highly problematic, in particular for the generalisation capability of pattern matching algorithms, as this means that data features for test data may be very different from the data the model is trained on. We propose an algorithmic solution to this problem by designing a neural net embedding architecture that transforms data from all the different sensor systems into a new common representation that works as well as if the training data and test data originated from the same sensor. The final algorithm result has an accuracy above 96 percent, and an AUC score above 0.99.

Margins are Insufficient for Explaining Gradient Boosting

Boosting is one of the most successful ideas in machine learning, achieving great practical performance with little fine-tuning. The success of boosted classifiers is most often attributed to improvements in margins. The focus on margin explanations was pioneered in the seminal work by Schapire et al. (1998) and has culminated in the $k$'th margin generalization bound by Gao and Zhou (2013), which was recently proved to be near-tight for some data distributions (Gronlund et al. 2019). In this work, we first demonstrate that the $k$'th margin bound is inadequate in explaining the performance of state-of-the-art gradient boosters. We then explain the short comings of the $k$'th margin bound and prove a stronger and more refined margin-based generalization bound for boosted classifiers that indeed succeeds in explaining the performance of modern gradient boosters. Finally, we improve upon the recent generalization lower bound by Gr{\o}nlund et al. (2019).

Near-Tight Margin-Based Generalization Bounds for Support Vector Machines

Support Vector Machines (SVMs) are among the most fundamental tools for binary classification. In its simplest formulation, an SVM produces a hyperplane separating two classes of data using the largest possible margin to the data. The focus on maximizing the margin has been well motivated through numerous generalization bounds. In this paper, we revisit and improve the classic generalization bounds in terms of margins. Furthermore, we complement our new generalization bound by a nearly matching lower bound, thus almost settling the generalization performance of SVMs in terms of margins.

Margin-Based Generalization Lower Bounds for Boosted Classifiers

Boosting is one of the most successful ideas in machine learning. The most well-accepted explanations for the low generalization error of boosting algorithms such as AdaBoost stem from margin theory. The study of margins in the context of boosting algorithms was initiated by Schapire, Freund, Bartlett and Lee (1998) and has inspired numerous boosting algorithms and generalization bounds. To date, the strongest known generalization (upper bound) is the $k$th margin bound of Gao and Zhou (2013). Despite the numerous generalization upper bounds that have been proved over the last two decades, nothing is known about the tightness of these bounds. In this paper, we give the first margin-based lower bounds on the generalization error of boosted classifiers. Our lower bounds nearly match the $k$th margin bound and thus almost settle the generalization performance of boosted classifiers in terms of margins.

Learning to Find Hydrological Corrections

High resolution Digital Elevation models, such as the (Big) grid terrain model of Denmark with more than 200 billion measurements, is a basic requirement for water flow modelling and flood risk analysis. However, a large number of modifications often need to be made to even very accurate terrain models, such as the Danish model, before they can be used in realistic flow modeling. These modifications include removal of bridges, which otherwise will act as dams in flow modeling, and inclusion of culverts that transport water underneath roads. In fact, the danish model is accompanied by a detailed set of hydrological corrections for the digital elevation model. However, producing these hydrological corrections is a very slow an expensive process, since it is to a large extent done manually and often with local input. This also means that corrections can be of varying quality. In this paper we propose a new algorithmic apporach based on machine learning and convolutional neural networks for automatically detecting hydrological corrections for such large terrain data. Our model is able to detect most hydrological corrections known for the danish model and quite a few more that should have been included in the original list.

Optimal Minimal Margin Maximization with Boosting

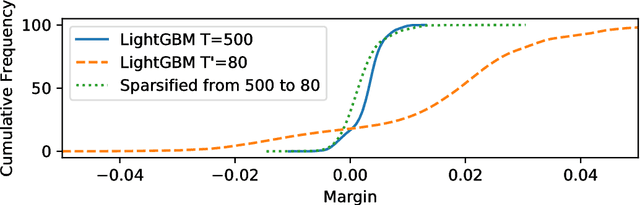
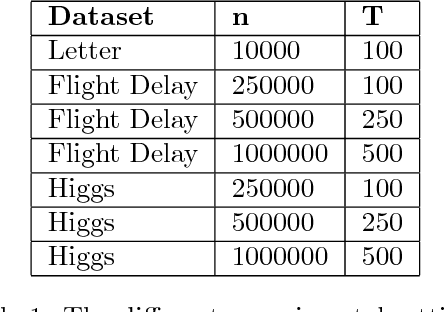
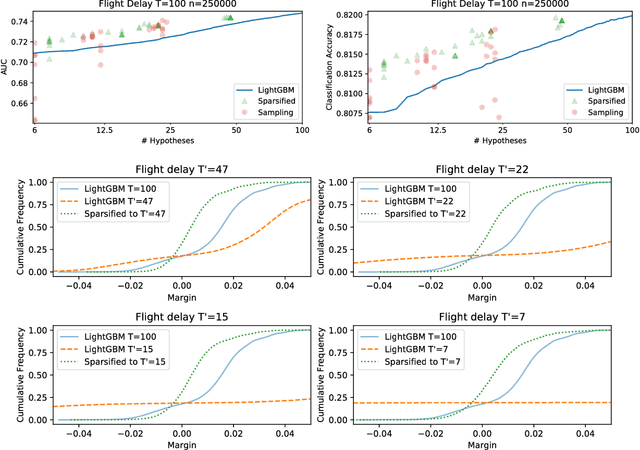
Boosting algorithms produce a classifier by iteratively combining base hypotheses. It has been observed experimentally that the generalization error keeps improving even after achieving zero training error. One popular explanation attributes this to improvements in margins. A common goal in a long line of research, is to maximize the smallest margin using as few base hypotheses as possible, culminating with the AdaBoostV algorithm by (R{\"a}tsch and Warmuth [JMLR'04]). The AdaBoostV algorithm was later conjectured to yield an optimal trade-off between number of hypotheses trained and the minimal margin over all training points (Nie et al. [JMLR'13]). Our main contribution is a new algorithm refuting this conjecture. Furthermore, we prove a lower bound which implies that our new algorithm is optimal.

Fast Exact k-Means, k-Medians and Bregman Divergence Clustering in 1D

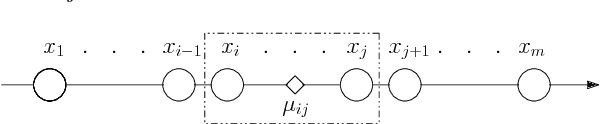
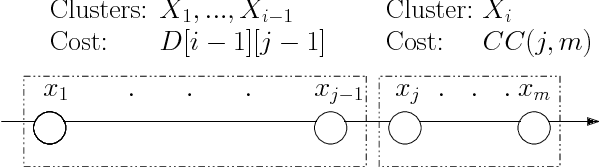
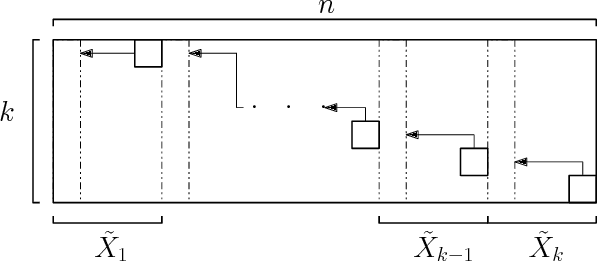
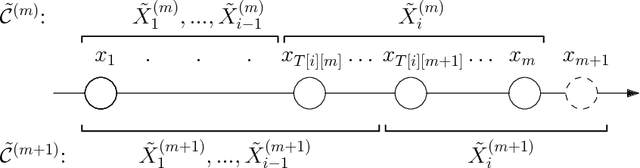
The $k$-Means clustering problem on $n$ points is NP-Hard for any dimension $d\ge 2$, however, for the 1D case there exists exact polynomial time algorithms. Previous literature reported an $O(kn^2)$ time dynamic programming algorithm that uses $O(kn)$ space. It turns out that the problem has been considered under a different name more than twenty years ago. We present all the existing work that had been overlooked and compare the various solutions theoretically. Moreover, we show how to reduce the space usage for some of them, as well as generalize them to data structures that can quickly report an optimal $k$-Means clustering for any $k$. Finally we also generalize all the algorithms to work for the absolute distance and to work for any Bregman Divergence. We complement our theoretical contributions by experiments that compare the practical performance of the various algorithms.