Optimal Minimal Margin Maximization with Boosting
Paper and Code
Jan 30, 2019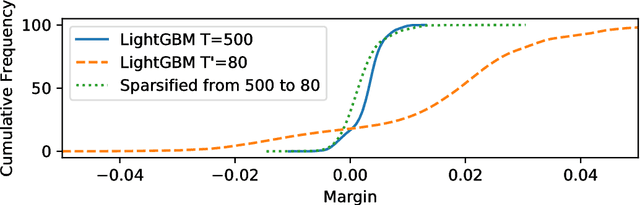
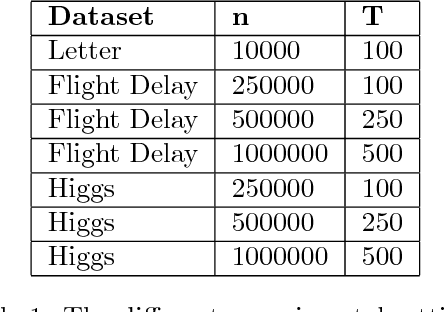

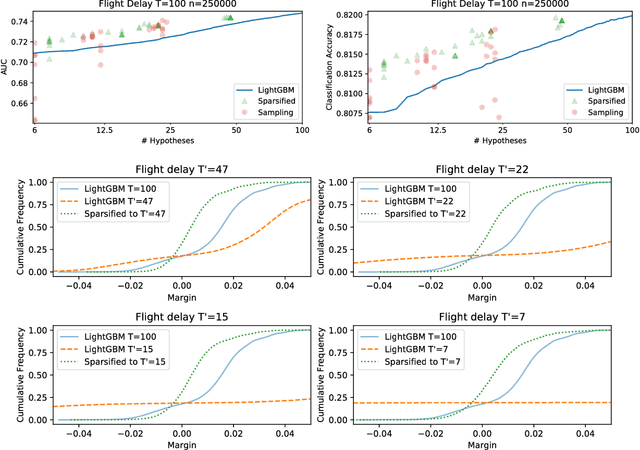
Boosting algorithms produce a classifier by iteratively combining base hypotheses. It has been observed experimentally that the generalization error keeps improving even after achieving zero training error. One popular explanation attributes this to improvements in margins. A common goal in a long line of research, is to maximize the smallest margin using as few base hypotheses as possible, culminating with the AdaBoostV algorithm by (R{\"a}tsch and Warmuth [JMLR'04]). The AdaBoostV algorithm was later conjectured to yield an optimal trade-off between number of hypotheses trained and the minimal margin over all training points (Nie et al. [JMLR'13]). Our main contribution is a new algorithm refuting this conjecture. Furthermore, we prove a lower bound which implies that our new algorithm is optimal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge