Reducing the Cost of Quantum Chemical Data By Backpropagating Through Density Functional Theory

Density Functional Theory (DFT) accurately predicts the quantum chemical properties of molecules, but scales as $O(N_{\text{electrons}}^3)$. Sch\"utt et al. (2019) successfully approximate DFT 1000x faster with Neural Networks (NN). Arguably, the biggest problem one faces when scaling to larger molecules is the cost of DFT labels. For example, it took years to create the PCQ dataset (Nakata & Shimazaki, 2017) on which subsequent NNs are trained within a week. DFT labels molecules by minimizing energy $E(\cdot )$ as a "loss function." We bypass dataset creation by directly training NNs with $E(\cdot )$ as a loss function. For comparison, Sch\"utt et al. (2019) spent 626 hours creating a dataset on which they trained their NN for 160h, for a total of 786h; our method achieves comparable performance within 31h.

Training and inference of large language models using 8-bit floating point

FP8 formats are gaining popularity to boost the computational efficiency for training and inference of large deep learning models. Their main challenge is that a careful choice of scaling is needed to prevent degradation due to the reduced dynamic range compared to higher-precision formats. Although there exists ample literature about selecting such scalings for INT formats, this critical aspect has yet to be addressed for FP8. This paper presents a methodology to select the scalings for FP8 linear layers, based on dynamically updating per-tensor scales for the weights, gradients and activations. We apply this methodology to train and validate large language models of the type of GPT and Llama 2 using FP8, for model sizes ranging from 111M to 70B. To facilitate the understanding of the FP8 dynamics, our results are accompanied by plots of the per-tensor scale distribution for weights, activations and gradients during both training and inference.

Tuple Packing: Efficient Batching of Small Graphs in Graph Neural Networks

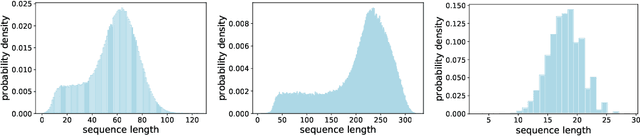
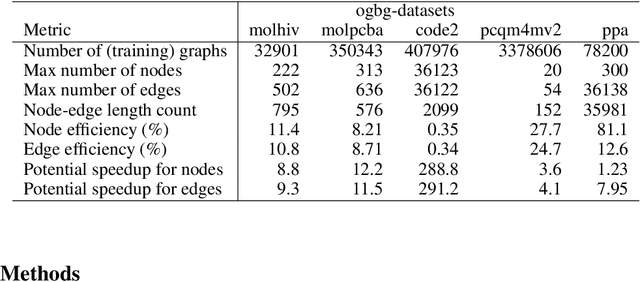
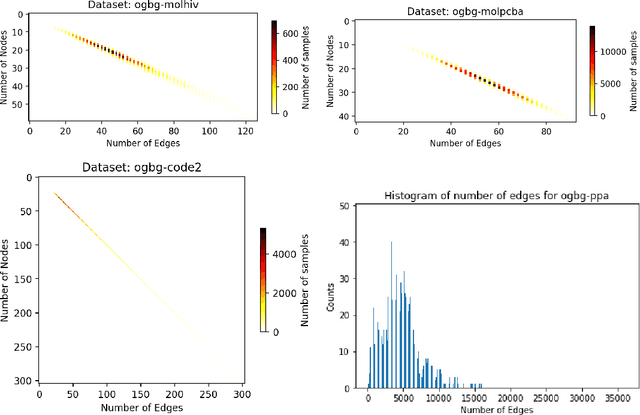
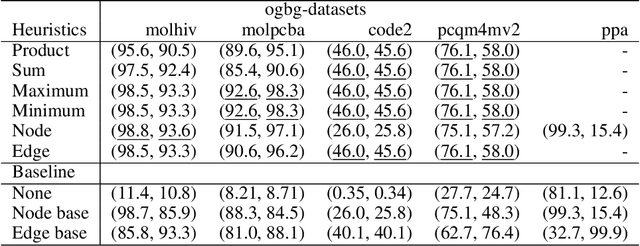
When processing a batch of graphs in machine learning models such as Graph Neural Networks (GNN), it is common to combine several small graphs into one overall graph to accelerate processing and remove or reduce the overhead of padding. This is for example supported in the PyG library. However, the sizes of small graphs can vary substantially with respect to the number of nodes and edges, and hence the size of the combined graph can still vary considerably, especially for small batch sizes. Therefore, the costs of excessive padding and wasted compute are still incurred when working with static shapes, which are preferred for maximum acceleration. This paper proposes a new hardware agnostic approach -- tuple packing -- for generating batches that cause minimal overhead. The algorithm extends recently introduced sequence packing approaches to work on the 2D tuples of (|nodes|, |edges|). A monotone heuristic is applied to the 2D histogram of tuple values to define a priority for packing histogram bins together with the objective to reach a limit on the number of nodes as well as the number of edges. Experiments verify the effectiveness of the algorithm on multiple datasets.

The Phong Surface: Efficient 3D Model Fitting using Lifted Optimization

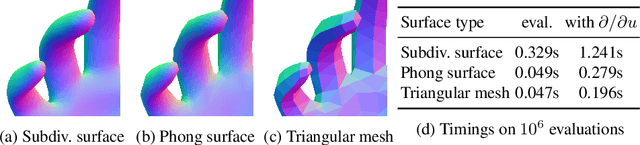
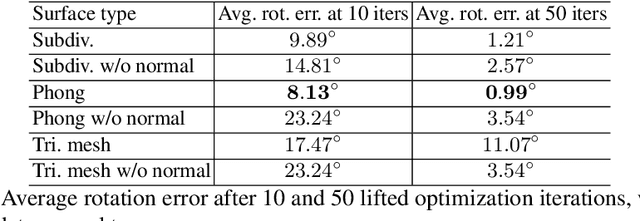
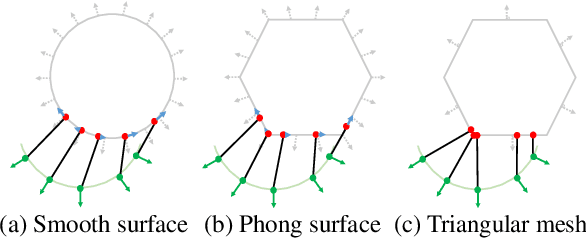
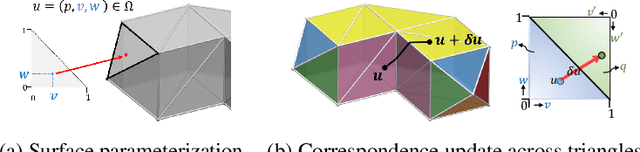
Realtime perceptual and interaction capabilities in mixed reality require a range of 3D tracking problems to be solved at low latency on resource-constrained hardware such as head-mounted devices. Indeed, for devices such as HoloLens 2 where the CPU and GPU are left available for applications, multiple tracking subsystems are required to run on a continuous, real-time basis while sharing a single Digital Signal Processor. To solve model-fitting problems for HoloLens 2 hand tracking, where the computational budget is approximately 100 times smaller than an iPhone 7, we introduce a new surface model: the `Phong surface'. Using ideas from computer graphics, the Phong surface describes the same 3D shape as a triangulated mesh model, but with continuous surface normals which enable the use of lifting-based optimization, providing significant efficiency gains over ICP-based methods. We show that Phong surfaces retain the convergence benefits of smoother surface models, while triangle meshes do not.