Principal Orthogonal Latent Components Analysis (POLCA Net)

Representation learning is a pivotal area in the field of machine learning, focusing on the development of methods to automatically discover the representations or features needed for a given task from raw data. Unlike traditional feature engineering, which requires manual crafting of features, representation learning aims to learn features that are more useful and relevant for tasks such as classification, prediction, and clustering. We introduce Principal Orthogonal Latent Components Analysis Network (POLCA Net), an approach to mimic and extend PCA and LDA capabilities to non-linear domains. POLCA Net combines an autoencoder framework with a set of specialized loss functions to achieve effective dimensionality reduction, orthogonality, variance-based feature sorting, high-fidelity reconstructions, and additionally, when used with classification labels, a latent representation well suited for linear classifiers and low dimensional visualization of class distribution as well.

Tuple Packing: Efficient Batching of Small Graphs in Graph Neural Networks

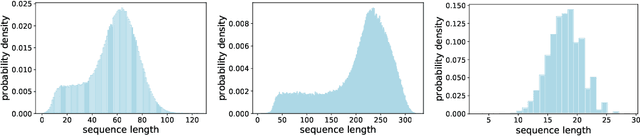
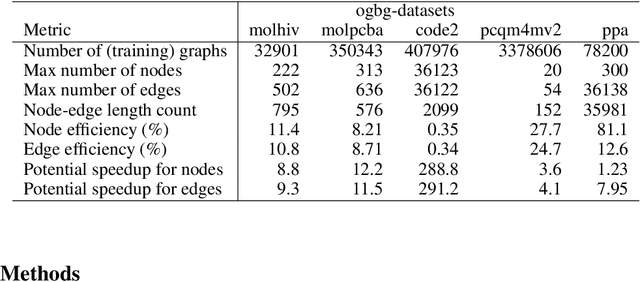
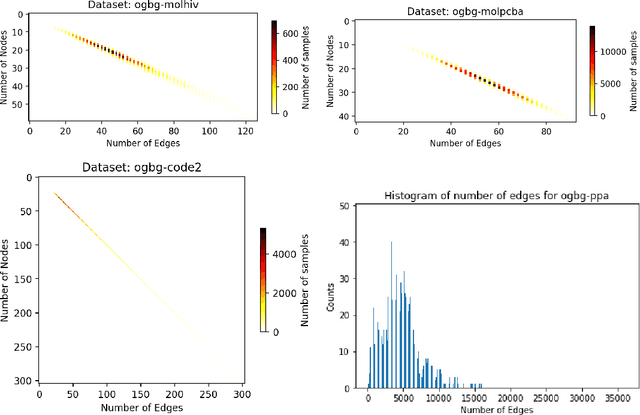
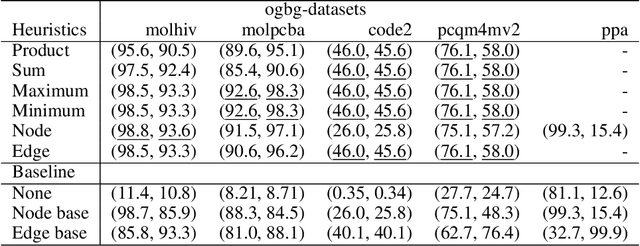
When processing a batch of graphs in machine learning models such as Graph Neural Networks (GNN), it is common to combine several small graphs into one overall graph to accelerate processing and remove or reduce the overhead of padding. This is for example supported in the PyG library. However, the sizes of small graphs can vary substantially with respect to the number of nodes and edges, and hence the size of the combined graph can still vary considerably, especially for small batch sizes. Therefore, the costs of excessive padding and wasted compute are still incurred when working with static shapes, which are preferred for maximum acceleration. This paper proposes a new hardware agnostic approach -- tuple packing -- for generating batches that cause minimal overhead. The algorithm extends recently introduced sequence packing approaches to work on the 2D tuples of (|nodes|, |edges|). A monotone heuristic is applied to the 2D histogram of tuple values to define a priority for packing histogram bins together with the objective to reach a limit on the number of nodes as well as the number of edges. Experiments verify the effectiveness of the algorithm on multiple datasets.