Meta Adaptive Task Sampling for Few-Domain Generalization

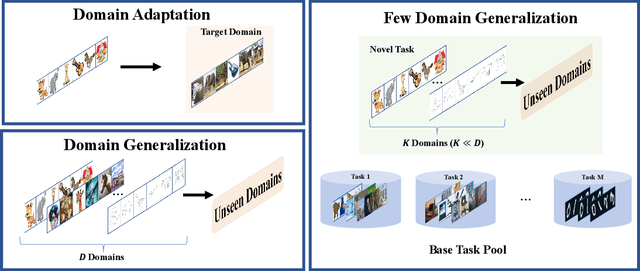
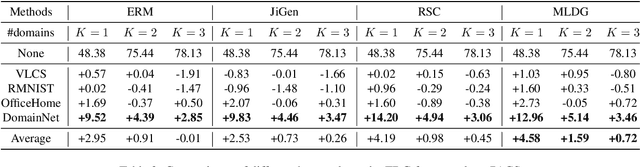
To ensure the out-of-distribution (OOD) generalization performance, traditional domain generalization (DG) methods resort to training on data from multiple sources with different underlying distributions. And the success of those DG methods largely depends on the fact that there are diverse training distributions. However, it usually needs great efforts to obtain enough heterogeneous data due to the high expenses, privacy issues or the scarcity of data. Thus an interesting yet seldom investigated problem arises: how to improve the OOD generalization performance when the perceived heterogeneity is limited. In this paper, we instantiate a new framework called few-domain generalization (FDG), which aims to learn a generalizable model from very few domains of novel tasks with the knowledge acquired from previous learning experiences on base tasks. Moreover, we propose a Meta Adaptive Task Sampling (MATS) procedure to differentiate base tasks according to their semantic and domain-shift similarity to the novel task. Empirically, we show that the newly introduced FDG framework can substantially improve the OOD generalization performance on the novel task and further combining MATS with episodic training could outperform several state-of-the-art DG baselines on widely used benchmarks like PACS and DomainNet.

Stable Learning via Sparse Variable Independence

The problem of covariate-shift generalization has attracted intensive research attention. Previous stable learning algorithms employ sample reweighting schemes to decorrelate the covariates when there is no explicit domain information about training data. However, with finite samples, it is difficult to achieve the desirable weights that ensure perfect independence to get rid of the unstable variables. Besides, decorrelating within stable variables may bring about high variance of learned models because of the over-reduced effective sample size. A tremendous sample size is required for these algorithms to work. In this paper, with theoretical justification, we propose SVI (Sparse Variable Independence) for the covariate-shift generalization problem. We introduce sparsity constraint to compensate for the imperfectness of sample reweighting under the finite-sample setting in previous methods. Furthermore, we organically combine independence-based sample reweighting and sparsity-based variable selection in an iterative way to avoid decorrelating within stable variables, increasing the effective sample size to alleviate variance inflation. Experiments on both synthetic and real-world datasets demonstrate the improvement of covariate-shift generalization performance brought by SVI.

Distributionally Invariant Learning: Rationalization and Practical Algorithms

The invariance property across environments is at the heart of invariant learning methods for the Out-of-Distribution (OOD) Generalization problem. Although intuitively reasonable, strong assumptions on the availability and quality of environments have to be made for the learnability of the strict invariance property. Recently, to relax the requirements for environments empirically, some works propose to learn pseudo-environments for invariant learning. However, it could be misleading when pursuing strict invariance under latent heterogeneity, since the underlying invariance could have been violated during the pseudo-environment learning procedure. To this end, we come up with the distributional invariance property as a relaxed alternative to the strict invariance, which considers the invariance only among sub-populations down to a prescribed scale and allows a certain degree of variation. We reformulate the invariant learning problem under latent heterogeneity into a relaxed form that pursues the distributional invariance, based on which we propose our novel Distributionally Invariant Learning (DIL) framework as well as two implementations named DIL-MMD and DIL-KL. Theoretically, we provide the guarantees for the distributional invariance as well as bounds of the generalization error gap. Extensive experimental results validate the effectiveness of our proposed algorithms.

NICO++: Towards Better Benchmarking for Domain Generalization

Despite the remarkable performance that modern deep neural networks have achieved on independent and identically distributed (I.I.D.) data, they can crash under distribution shifts. Most current evaluation methods for domain generalization (DG) adopt the leave-one-out strategy as a compromise on the limited number of domains. We propose a large-scale benchmark with extensive labeled domains named NICO++ along with more rational evaluation methods for comprehensively evaluating DG algorithms. To evaluate DG datasets, we propose two metrics to quantify covariate shift and concept shift, respectively. Two novel generalization bounds from the perspective of data construction are proposed to prove that limited concept shift and significant covariate shift favor the evaluation capability for generalization. Through extensive experiments, NICO++ shows its superior evaluation capability compared with current DG datasets and its contribution in alleviating unfairness caused by the leak of oracle knowledge in model selection.

Regulatory Instruments for Fair Personalized Pricing

Personalized pricing is a business strategy to charge different prices to individual consumers based on their characteristics and behaviors. It has become common practice in many industries nowadays due to the availability of a growing amount of high granular consumer data. The discriminatory nature of personalized pricing has triggered heated debates among policymakers and academics on how to design regulation policies to balance market efficiency and equity. In this paper, we propose two sound policy instruments, i.e., capping the range of the personalized prices or their ratios. We investigate the optimal pricing strategy of a profit-maximizing monopoly under both regulatory constraints and the impact of imposing them on consumer surplus, producer surplus, and social welfare. We theoretically prove that both proposed constraints can help balance consumer surplus and producer surplus at the expense of total surplus for common demand distributions, such as uniform, logistic, and exponential distributions. Experiments on both simulation and real-world datasets demonstrate the correctness of these theoretical results. Our findings and insights shed light on regulatory policy design for the increasingly monopolized business in the digital era.

Why Stable Learning Works? A Theory of Covariate Shift Generalization

Covariate shift generalization, a typical case in out-of-distribution (OOD) generalization, requires a good performance on the unknown testing distribution, which varies from the accessible training distribution in the form of covariate shift. Recently, stable learning algorithms have shown empirical effectiveness to deal with covariate shift generalization on several learning models involving regression algorithms and deep neural networks. However, the theoretical explanations for such effectiveness are still missing. In this paper, we take a step further towards the theoretical analysis of stable learning algorithms by explaining them as feature selection processes. We first specify a set of variables, named minimal stable variable set, that is minimal and optimal to deal with covariate shift generalization for common loss functions, including the mean squared loss and binary cross entropy loss. Then we prove that under ideal conditions, stable learning algorithms could identify the variables in this set. Further analysis on asymptotic properties and error propagation are also provided. These theories shed light on why stable learning works for covariate shift generalization.

Kernelized Heterogeneous Risk Minimization

The ability to generalize under distributional shifts is essential to reliable machine learning, while models optimized with empirical risk minimization usually fail on non-$i.i.d$ testing data. Recently, invariant learning methods for out-of-distribution (OOD) generalization propose to find causally invariant relationships with multi-environments. However, modern datasets are frequently multi-sourced without explicit source labels, rendering many invariant learning methods inapplicable. In this paper, we propose Kernelized Heterogeneous Risk Minimization (KerHRM) algorithm, which achieves both the latent heterogeneity exploration and invariant learning in kernel space, and then gives feedback to the original neural network by appointing invariant gradient direction. We theoretically justify our algorithm and empirically validate the effectiveness of our algorithm with extensive experiments.

Towards Out-Of-Distribution Generalization: A Survey

Classic machine learning methods are built on the $i.i.d.$ assumption that training and testing data are independent and identically distributed. However, in real scenarios, the $i.i.d.$ assumption can hardly be satisfied, rendering the sharp drop of classic machine learning algorithms' performances under distributional shifts, which indicates the significance of investigating the Out-of-Distribution generalization problem. Out-of-Distribution (OOD) generalization problem addresses the challenging setting where the testing distribution is unknown and different from the training. This paper serves as the first effort to systematically and comprehensively discuss the OOD generalization problem, from the definition, methodology, evaluation to the implications and future directions. Firstly, we provide the formal definition of the OOD generalization problem. Secondly, existing methods are categorized into three parts based on their positions in the whole learning pipeline, namely unsupervised representation learning, supervised model learning and optimization, and typical methods for each category are discussed in detail. We then demonstrate the theoretical connections of different categories, and introduce the commonly used datasets and evaluation metrics. Finally, we summarize the whole literature and raise some future directions for OOD generalization problem. The summary of OOD generalization methods reviewed in this survey can be found at http://out-of-distribution-generalization.com.

Domain-Irrelevant Representation Learning for Unsupervised Domain Generalization

Domain generalization (DG) aims to help models trained on a set of source domains generalize better on unseen target domains. The performances of current DG methods largely rely on sufficient labeled data, which however are usually costly or unavailable. While unlabeled data are far more accessible, we seek to explore how unsupervised learning can help deep models generalizes across domains. Specifically, we study a novel generalization problem called unsupervised domain generalization, which aims to learn generalizable models with unlabeled data. Furthermore, we propose a Domain-Irrelevant Unsupervised Learning (DIUL) method to cope with the significant and misleading heterogeneity within unlabeled data and severe distribution shifts between source and target data. Surprisingly we observe that DIUL can not only counterbalance the scarcity of labeled data but also further strengthen the generalization ability of models when the labeled data are sufficient. As a pretraining approach, DIUL shows superior to ImageNet pretraining protocol even when the available data are unlabeled and of a greatly smaller amount compared to ImageNet. Extensive experiments clearly demonstrate the effectiveness of our method compared with state-of-the-art unsupervised learning counterparts.

Distributionally Robust Learning with Stable Adversarial Training

Machine learning algorithms with empirical risk minimization are vulnerable under distributional shifts due to the greedy adoption of all the correlations found in training data. There is an emerging literature on tackling this problem by minimizing the worst-case risk over an uncertainty set. However, existing methods mostly construct ambiguity sets by treating all variables equally regardless of the stability of their correlations with the target, resulting in the overwhelmingly-large uncertainty set and low confidence of the learner. In this paper, we propose a novel Stable Adversarial Learning (SAL) algorithm that leverages heterogeneous data sources to construct a more practical uncertainty set and conduct differentiated robustness optimization, where covariates are differentiated according to the stability of their correlations with the target. We theoretically show that our method is tractable for stochastic gradient-based optimization and provide the performance guarantees for our method. Empirical studies on both simulation and real datasets validate the effectiveness of our method in terms of uniformly good performance across unknown distributional shifts.