Partial Fairness Awareness: Belief-Guided Strategic Mechanism for Strategic Agents

Strategic machine learning investigates scenarios where agents manipulate their features to receive favorable decisions from predictive models. To address fairness concerns intrinsic to strategic classification, recent work has introduced group-specific fairness constraints. However, current fairness-aware approaches face a fundamental dilemma in the issue of fairness exposure: making these constraints public enables strategic manipulation and can lead to fairness reversal, while keeping them hidden may reduce social welfare and discourage genuine improvement. To fill this gap, we subsequently propose the problem of partial fairness awareness (PFA), as our theoretical analysis informs that such a dilemma can be mitigated by releasing the candidate set of fairness constraints and concealing the grounding constraint. To be specific, we introduce a belief-guided strategic mechanism, wherein agents iteratively interact with the decision system and maintain a belief distribution over the candidate set of fairness constraints. This belief-guided process enables agents, through iterative interaction and feedback, to update their belief distribution over the candidate set, thereby gradually aligning their belief with the grounding fairness constraint employed by the system. Extensive experiments on real-world and synthetic datasets demonstrate that PFA achieves lower group fairness gaps, higher acceptance of truly qualified individuals, and more stable outcomes compared to fully public or private fairness regimes.

Beyond Independent Manipulation: Individual Fairness-aware Strategic Classification with Peer Imitation

Strategic classification (SC) investigates scenarios where agents manipulate their features to obtain favorable decisions from predictive models. Existing fairness-aware SC approaches primarily focus on group fairness and typically assume that agents respond independently. However, when individual fairness is required, ensuring similar individuals receive similar outcomes, agents' manipulation becomes interdependent: an agent's preferred manipulation depends on the neighborhoods' outcomes. This induces a mismatch between classical SC formulations and fairness-aware decision settings, where independent models no longer accurately characterize strategic manipulations. To address this issue, we introduce individual fairness-aware strategic classification (IFSC), a framework that models peer-driven manipulation arising from individual fairness, where agents imitate nearby positively decided peers to obtain favorable outcomes. IFSC characterizes strategic manipulation as similarity-based imitation toward visible accepted peers and learns classifiers under the resulting post-manipulation distributions. To account for uncertainty in peer observability, IFSC employs a robust learning process that introduces stochastic perturbations during manipulation simulation. Experiments on synthetic and real-world datasets demonstrate that IFSC improves individual-fairness consistency and mitigates imitation-induced distortions.

Revisiting Zeroth-Order Hessian Approximation: A Single-Step Policy Optimization Lens

Accurate Zeroth-Order (ZO) Hessian estimation is a cornerstone of derivative-free methods, essential for tasks such as bilevel optimization, Bayesian inference, and uncertainty quantification. However, obtaining a complete suite of low-variance estimators for the Hessian and its inverse in high-dimensional settings remains a significant challenge. To address this, we propose a unified framework that reinterprets ZO Hessian approximation through the lens of single-step Policy Optimization (PO). This perspective establishes a theoretical equivalence between general ZO Hessian estimators and the Hessian of a smoothed PO objective, unifying distinct classical randomized estimators as specific instances of baseline selection. Building on this foundation, we introduce ZoVH, a comprehensive suite of variance-reduced estimators for the full Hessian matrix, its regularized inverse, and the bias-corrected inverse Hessian-gradient product. ZoVH leverages two key techniques: (1) a unique optimal baseline derived to provably minimize variance, and (2) a query reuse strategy that incorporates historical function queries to enhance sample efficiency without inflating costs. Our rigorous theoretical analysis confirms the unbiasedness of the Hessian estimator, validates the variance optimality of our baseline, provides error bounds for the entire ZoVH suite, and establishes convergence guarantees for the resulting curvature-aware ZO algorithm. Extensive empirical results validate our theoretical findings, demonstrating that ZoVH achieves superior estimation accuracy and convergence performance in real-world applications. Code is available at https://github.com/Qjbtiger/ZoVH

Beyond Rational Illusion: Behaviorally Realistic Strategic Classification

Strategic classification(SC) studies the interaction between decision models and agents who strategically manipulate their features for favorable outcomes. Existing SC frameworks typically rely on the idealized assumption that agents are strictly rational. However, evidence from behavioral economics and psychology consistently shows that real-world decision-making is often shaped by cognitive biases, deviating from pure rationality. To formalize this limitation, we identify and define a new problem setting, termed the behaviorally realistic strategic classification problem, where agents' strategic manipulations deviate from full rationality due to psychological biases. Motivated by the identified limitation, we propose the Prospect-Guided Strategic Framework (Pro-SF) to address the problem, a principled framework grounded in prospect theory to model and learn under behaviorally realistic strategic responses. Specifically, to capture behaviorally realistic strategic manipulations, our framework reformulates the Stackelberg-style interaction between agents and the decision-maker by incorporating three key mechanisms inspired by prospect theory, including the asymmetry between benefits and costs, different subjective reference points, and non-rational probability distortion. Experiments on synthetic and real-world datasets establish Pro-SF as a behaviorally grounded approach to strategic classification, bridging machine learning and behavioral economics for more reliable deployment in the real world.

When Tabular Foundation Models Meet Strategic Tabular Data: A Prior Alignment Approach

Tabular foundation models based on pretrained prior-data fitted networks~(PFNs) have shown strong generalization on diverse tabular tasks, but they are typically designed for \emph{non-strategic} settings where data distributions are independent of deployed classifiers. In many real-world decision scenarios, however, individuals may strategically modify their features after deployment to obtain favorable outcomes, inducing a post-deployment distribution shift. This paper studies whether PFN-style tabular foundation models can generalize to such \emph{strategic} tabular data. We show that strategic manipulation creates a mismatch between the non-strategic prior learned during pretraining and the post-manipulation strategic prior, which leads to systematic prediction bias. To address this issue, we propose \textbf{Strategic Prior-data Fitted Network}~\textit{(SPN)}, an inference-time strategy-aware framework that adapts tabular foundation models to strategic environments without retraining. SPN constructs strategic in-context examples to approximate post-manipulation inputs and aligns PFN predictions with the induced strategic distribution. Experiments on real-world and synthetic tabular datasets show that SPN consistently improves robustness and predictive performance under strategic manipulation compared with both tabular foundation models and classical tabular methods.

LimiX: Unleashing Structured-Data Modeling Capability for Generalist Intelligence

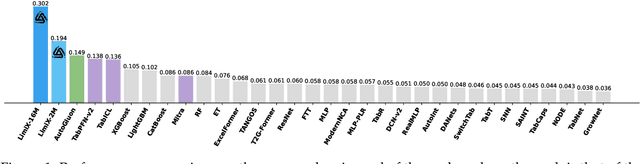
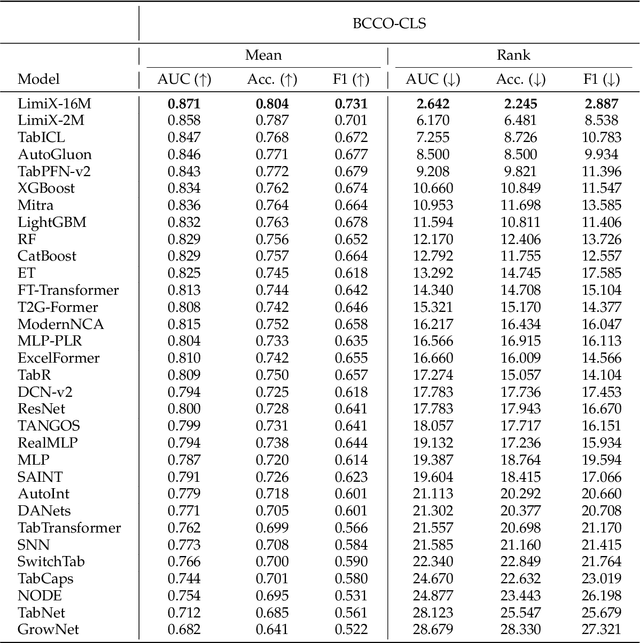
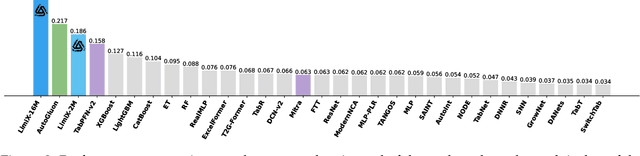
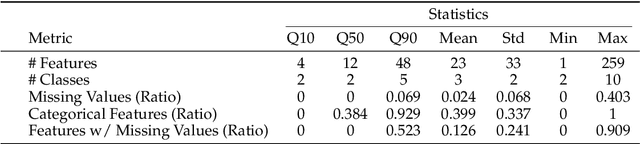
We argue that progress toward general intelligence requires complementary foundation models grounded in language, the physical world, and structured data. This report presents LimiX, the first installment of our large structured-data models (LDMs). LimiX treats structured data as a joint distribution over variables and missingness, thus capable of addressing a wide range of tabular tasks through query-based conditional prediction via a single model. LimiX is pretrained using masked joint-distribution modeling with an episodic, context-conditional objective, where the model predicts for query subsets conditioned on dataset-specific contexts, supporting rapid, training-free adaptation at inference. We evaluate LimiX across 10 large structured-data benchmarks with broad regimes of sample size, feature dimensionality, class number, categorical-to-numerical feature ratio, missingness, and sample-to-feature ratios. With a single model and a unified interface, LimiX consistently surpasses strong baselines including gradient-boosting trees, deep tabular networks, recent tabular foundation models, and automated ensembles, as shown in Figure 1 and Figure 2. The superiority holds across a wide range of tasks, such as classification, regression, missing value imputation, and data generation, often by substantial margins, while avoiding task-specific architectures or bespoke training per task. All LimiX models are publicly accessible under Apache 2.0.

Heterogeneous Data Game: Characterizing the Model Competition Across Multiple Data Sources

Data heterogeneity across multiple sources is common in real-world machine learning (ML) settings. Although many methods focus on enabling a single model to handle diverse data, real-world markets often comprise multiple competing ML providers. In this paper, we propose a game-theoretic framework -- the Heterogeneous Data Game -- to analyze how such providers compete across heterogeneous data sources. We investigate the resulting pure Nash equilibria (PNE), showing that they can be non-existent, homogeneous (all providers converge on the same model), or heterogeneous (providers specialize in distinct data sources). Our analysis spans monopolistic, duopolistic, and more general markets, illustrating how factors such as the "temperature" of data-source choice models and the dominance of certain data sources shape equilibrium outcomes. We offer theoretical insights into both homogeneous and heterogeneous PNEs, guiding regulatory policies and practical strategies for competitive ML marketplaces.

COUNTS: Benchmarking Object Detectors and Multimodal Large Language Models under Distribution Shifts

Current object detectors often suffer significant perfor-mance degradation in real-world applications when encountering distributional shifts. Consequently, the out-of-distribution (OOD) generalization capability of object detectors has garnered increasing attention from researchers. Despite this growing interest, there remains a lack of a large-scale, comprehensive dataset and evaluation benchmark with fine-grained annotations tailored to assess the OOD generalization on more intricate tasks like object detection and grounding. To address this gap, we introduce COUNTS, a large-scale OOD dataset with object-level annotations. COUNTS encompasses 14 natural distributional shifts, over 222K samples, and more than 1,196K labeled bounding boxes. Leveraging COUNTS, we introduce two novel benchmarks: O(OD)2 and OODG. O(OD)2 is designed to comprehensively evaluate the OOD generalization capabilities of object detectors by utilizing controlled distribution shifts between training and testing data. OODG, on the other hand, aims to assess the OOD generalization of grounding abilities in multimodal large language models (MLLMs). Our findings reveal that, while large models and extensive pre-training data substantially en hance performance in in-distribution (IID) scenarios, significant limitations and opportunities for improvement persist in OOD contexts for both object detectors and MLLMs. In visual grounding tasks, even the advanced GPT-4o and Gemini-1.5 only achieve 56.7% and 28.0% accuracy, respectively. We hope COUNTS facilitates advancements in the development and assessment of robust object detectors and MLLMs capable of maintaining high performance under distributional shifts.

Understanding the Generalization of In-Context Learning in Transformers: An Empirical Study

Large language models (LLMs) like GPT-4 and LLaMA-3 utilize the powerful in-context learning (ICL) capability of Transformer architecture to learn on the fly from limited examples. While ICL underpins many LLM applications, its full potential remains hindered by a limited understanding of its generalization boundaries and vulnerabilities. We present a systematic investigation of transformers' generalization capability with ICL relative to training data coverage by defining a task-centric framework along three dimensions: inter-problem, intra-problem, and intra-task generalization. Through extensive simulation and real-world experiments, encompassing tasks such as function fitting, API calling, and translation, we find that transformers lack inter-problem generalization with ICL, but excel in intra-task and intra-problem generalization. When the training data includes a greater variety of mixed tasks, it significantly enhances the generalization ability of ICL on unseen tasks and even on known simple tasks. This guides us in designing training data to maximize the diversity of tasks covered and to combine different tasks whenever possible, rather than solely focusing on the target task for testing.

Sample Weight Averaging for Stable Prediction

The challenge of Out-of-Distribution (OOD) generalization poses a foundational concern for the application of machine learning algorithms to risk-sensitive areas. Inspired by traditional importance weighting and propensity weighting methods, prior approaches employ an independence-based sample reweighting procedure. They aim at decorrelating covariates to counteract the bias introduced by spurious correlations between unstable variables and the outcome, thus enhancing generalization and fulfilling stable prediction under covariate shift. Nonetheless, these methods are prone to experiencing an inflation of variance, primarily attributable to the reduced efficacy in utilizing training samples during the reweighting process. Existing remedies necessitate either environmental labels or substantially higher time costs along with additional assumptions and supervised information. To mitigate this issue, we propose SAmple Weight Averaging (SAWA), a simple yet efficacious strategy that can be universally integrated into various sample reweighting algorithms to decrease the variance and coefficient estimation error, thus boosting the covariate-shift generalization and achieving stable prediction across different environments. We prove its rationality and benefits theoretically. Experiments across synthetic datasets and real-world datasets consistently underscore its superiority against covariate shift.