Safe Reinforcement Learning by Imagining the Near Future

Safe reinforcement learning is a promising path toward applying reinforcement learning algorithms to real-world problems, where suboptimal behaviors may lead to actual negative consequences. In this work, we focus on the setting where unsafe states can be avoided by planning ahead a short time into the future. In this setting, a model-based agent with a sufficiently accurate model can avoid unsafe states. We devise a model-based algorithm that heavily penalizes unsafe trajectories, and derive guarantees that our algorithm can avoid unsafe states under certain assumptions. Experiments demonstrate that our algorithm can achieve competitive rewards with fewer safety violations in several continuous control tasks.

Learning Barrier Certificates: Towards Safe Reinforcement Learning with Zero Training-time Violations

Training-time safety violations have been a major concern when we deploy reinforcement learning algorithms in the real world. This paper explores the possibility of safe RL algorithms with zero training-time safety violations in the challenging setting where we are only given a safe but trivial-reward initial policy without any prior knowledge of the dynamics model and additional offline data. We propose an algorithm, Co-trained Barrier Certificate for Safe RL (CRABS), which iteratively learns barrier certificates, dynamics models, and policies. The barrier certificates, learned via adversarial training, ensure the policy's safety assuming calibrated learned dynamics model. We also add a regularization term to encourage larger certified regions to enable better exploration. Empirical simulations show that zero safety violations are already challenging for a suite of simple environments with only 2-4 dimensional state space, especially if high-reward policies have to visit regions near the safety boundary. Prior methods require hundreds of violations to achieve decent rewards on these tasks, whereas our proposed algorithms incur zero violations.

Towards Learning to Play Piano with Dexterous Hands and Touch

The virtuoso plays the piano with passion, poetry and extraordinary technical ability. As Liszt said (a virtuoso)must call up scent and blossom, and breathe the breath of life. The strongest robots that can play a piano are based on a combination of specialized robot hands/piano and hardcoded planning algorithms. In contrast to that, in this paper, we demonstrate how an agent can learn directly from machine-readable music score to play the piano with dexterous hands on a simulated piano using reinforcement learning (RL) from scratch. We demonstrate the RL agents can not only find the correct key position but also deal with various rhythmic, volume and fingering, requirements. We achieve this by using a touch-augmented reward and a novel curriculum of tasks. We conclude by carefully studying the important aspects to enable such learning algorithms and that can potentially shed light on future research in this direction.

Towards Resolving the Implicit Bias of Gradient Descent for Matrix Factorization: Greedy Low-Rank Learning

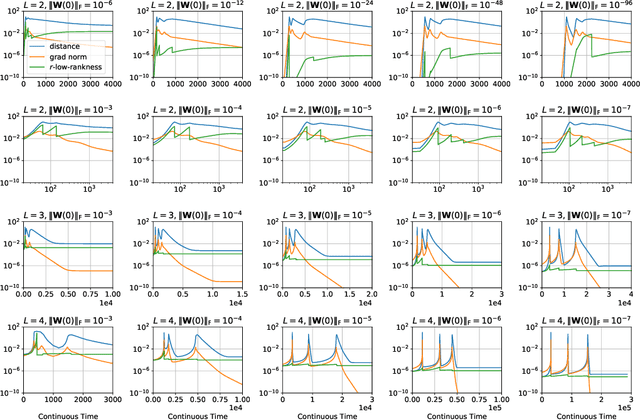
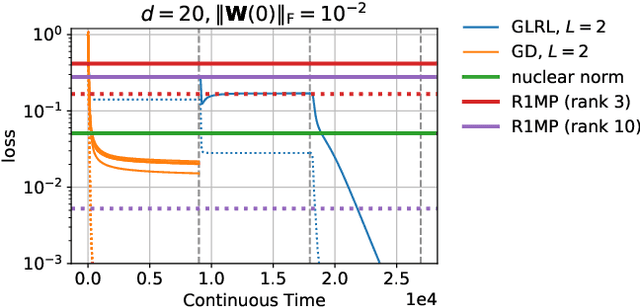
Matrix factorization is a simple and natural test-bed to investigate the implicit regularization of gradient descent. Gunasekar et al. (2018) conjectured that Gradient Flow with infinitesimal initialization converges to the solution that minimizes the nuclear norm, but a series of recent papers argued that the language of norm minimization is not sufficient to give a full characterization for the implicit regularization. In this work, we provide theoretical and empirical evidence that for depth-2 matrix factorization, gradient flow with infinitesimal initialization is mathematically equivalent to a simple heuristic rank minimization algorithm, Greedy Low-Rank Learning, under some reasonable assumptions. This generalizes the rank minimization view from previous works to a much broader setting and enables us to construct counter-examples to refute the conjecture from Gunasekar et al. (2018). We also extend the results to the case where depth $\ge 3$, and we show that the benefit of being deeper is that the above convergence has a much weaker dependence over initialization magnitude so that this rank minimization is more likely to take effect for initialization with practical scale.

Provable Representation Learning for Imitation Learning via Bi-level Optimization

A common strategy in modern learning systems is to learn a representation that is useful for many tasks, a.k.a. representation learning. We study this strategy in the imitation learning setting for Markov decision processes (MDPs) where multiple experts' trajectories are available. We formulate representation learning as a bi-level optimization problem where the "outer" optimization tries to learn the joint representation and the "inner" optimization encodes the imitation learning setup and tries to learn task-specific parameters. We instantiate this framework for the imitation learning settings of behavior cloning and observation-alone. Theoretically, we show using our framework that representation learning can provide sample complexity benefits for imitation learning in both settings. We also provide proof-of-concept experiments to verify our theory.

Bootstrapping the Expressivity with Model-based Planning

We compare the model-free reinforcement learning with the model-based approaches through the lens of the expressive power of neural networks for policies, $Q$-functions, and dynamics. We show, theoretically and empirically, that even for one-dimensional continuous state space, there are many MDPs whose optimal $Q$-functions and policies are much more complex than the dynamics. We hypothesize many real-world MDPs also have a similar property. For these MDPs, model-based planning is a favorable algorithm, because the resulting policies can approximate the optimal policy significantly better than a neural network parameterization can, and model-free or model-based policy optimization rely on policy parameterization. Motivated by the theory, we apply a simple multi-step model-based bootstrapping planner (BOOTS) to bootstrap a weak $Q$-function into a stronger policy. Empirical results show that applying BOOTS on top of model-based or model-free policy optimization algorithms at the test time improves the performance on MuJoCo benchmark tasks.

Learning Self-Correctable Policies and Value Functions from Demonstrations with Negative Sampling

Imitation learning, followed by reinforcement learning algorithms, is a promising paradigm to solve complex control tasks sample-efficiently. However, learning from demonstrations often suffers from the covariate shift problem, which results in cascading errors of the learned policy. We introduce a notion of conservatively-extrapolated value functions, which provably lead to policies with self-correction. We design an algorithm Value Iteration with Negative Sampling (VINS) that practically learns such value functions with conservative extrapolation. We show that VINS can correct mistakes of the behavioral cloning policy on simulated robotics benchmark tasks. We also propose the algorithm of using VINS to initialize a reinforcement learning algorithm, which is shown to outperform significantly prior works in sample efficiency.

Provably Efficient $Q$-learning with Function Approximation via Distribution Shift Error Checking Oracle

$Q$-learning with function approximation is one of the most popular methods in reinforcement learning. Though the idea of using function approximation was proposed at least $60$ years ago, even in the simplest setup, i.e, approximating $Q$-functions with linear functions, it is still an open problem how to design a provably efficient algorithm that learns a near-optimal policy. The key challenges are how to efficiently explore the state space and how to decide when to stop exploring in conjunction with the function approximation scheme. The current paper presents a provably efficient algorithm for $Q$-learning with linear function approximation. Under certain regularity assumptions, our algorithm, Difference Maximization $Q$-learning (DMQ), combined with linear function approximation, returns a near optimal policy using polynomial number of trajectories. Our algorithm introduces a new notion, the Distribution Shift Error Checking (DSEC) oracle. This oracle tests whether there exists a function in the function class that predicts well on a distribution $\mathcal{D}_1$, but predicts poorly on another distribution $\mathcal{D}_2$, where $\mathcal{D}_1$ and $\mathcal{D}_2$ are distributions over states induced by two different exploration policies. For the linear function class, this oracle is equivalent to solving a top eigenvalue problem. We believe our algorithmic insights, especially the DSEC oracle, are also useful in designing and analyzing reinforcement learning algorithms with general function approximation.

Implicit Regularization in Deep Matrix Factorization

Efforts to understand the generalization mystery in deep learning have led to the belief that gradient-based optimization induces a form of implicit regularization, a bias towards models of low "complexity." We study the implicit regularization of gradient descent over deep linear neural networks for matrix completion and sensing, a model referred to as deep matrix factorization. Our first finding, supported by theory and experiments, is that adding depth to a matrix factorization enhances an implicit tendency towards low-rank solutions, oftentimes leading to more accurate recovery. Secondly, we present theoretical and empirical arguments questioning a nascent view by which implicit regularization in matrix factorization can be captured using simple mathematical norms. Our results point to the possibility that the language of standard regularizers may not be rich enough to fully encompass the implicit regularization brought forth by gradient-based optimization.

Algorithmic Framework for Model-based Deep Reinforcement Learning with Theoretical Guarantees

Model-based reinforcement learning (RL) is considered to be a promising approach to reduce the sample complexity that hinders model-free RL. However, the theoretical understanding of such methods has been rather limited. This paper introduces a novel algorithmic framework for designing and analyzing model-based RL algorithms with theoretical guarantees. We design a meta-algorithm with a theoretical guarantee of monotone improvement to a local maximum of the expected reward. The meta-algorithm iteratively builds a lower bound of the expected reward based on the estimated dynamical model and sample trajectories, and then maximizes the lower bound jointly over the policy and the model. The framework extends the optimism-in-face-of-uncertainty principle to non-linear dynamical models in a way that requires no explicit uncertainty quantification. Instantiating our framework with simplification gives a variant of model-based RL algorithms Stochastic Lower Bounds Optimization (SLBO). Experiments demonstrate that SLBO achieves state-of-the-art performance when only one million or fewer samples are permitted on a range of continuous control benchmark tasks.