SmileSplat: Generalizable Gaussian Splats for Unconstrained Sparse Images

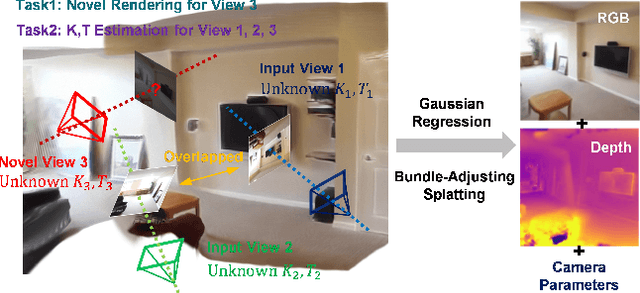
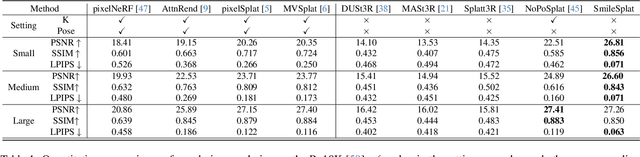
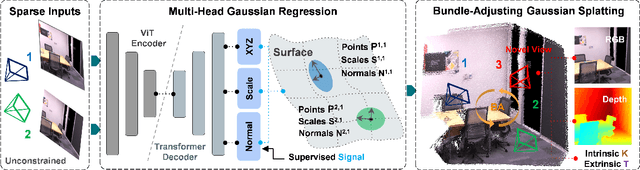
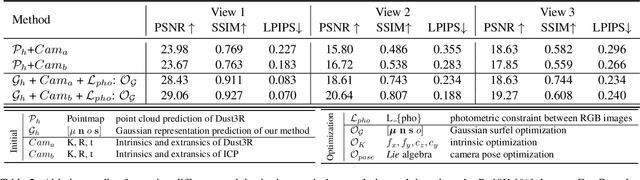
Sparse Multi-view Images can be Learned to predict explicit radiance fields via Generalizable Gaussian Splatting approaches, which can achieve wider application prospects in real-life when ground-truth camera parameters are not required as inputs. In this paper, a novel generalizable Gaussian Splatting method, SmileSplat, is proposed to reconstruct pixel-aligned Gaussian surfels for diverse scenarios only requiring unconstrained sparse multi-view images. First, Gaussian surfels are predicted based on the multi-head Gaussian regression decoder, which can are represented with less degree-of-freedom but have better multi-view consistency. Furthermore, the normal vectors of Gaussian surfel are enhanced based on high-quality of normal priors. Second, the Gaussians and camera parameters (both extrinsic and intrinsic) are optimized to obtain high-quality Gaussian radiance fields for novel view synthesis tasks based on the proposed Bundle-Adjusting Gaussian Splatting module. Extensive experiments on novel view rendering and depth map prediction tasks are conducted on public datasets, demonstrating that the proposed method achieves state-of-the-art performance in various 3D vision tasks. More information can be found on our project page (https://yanyan-li.github.io/project/gs/smilesplat)

LiLoc: Lifelong Localization using Adaptive Submap Joining and Egocentric Factor Graph

This paper proposes a versatile graph-based lifelong localization framework, LiLoc, which enhances its timeliness by maintaining a single central session while improves the accuracy through multi-modal factors between the central and subsidiary sessions. First, an adaptive submap joining strategy is employed to generate prior submaps (keyframes and poses) for the central session, and to provide priors for subsidiaries when constraints are needed for robust localization. Next, a coarse-to-fine pose initialization for subsidiary sessions is performed using vertical recognition and ICP refinement in the global coordinate frame. To elevate the accuracy of subsequent localization, we propose an egocentric factor graph (EFG) module that integrates the IMU preintegration, LiDAR odometry and scan match factors in a joint optimization manner. Specifically, the scan match factors are constructed by a novel propagation model that efficiently distributes the prior constrains as edges to the relevant prior pose nodes, weighted by noises based on keyframe registration errors. Additionally, the framework supports flexible switching between two modes: relocalization (RLM) and incremental localization (ILM) based on the proposed overlap-based mechanism to select or update the prior submaps from central session. The proposed LiLoc is tested on public and custom datasets, demonstrating accurate localization performance against state-of-the-art methods. Our codes will be publicly available on https://github.com/Yixin-F/LiLoc.

Solving the Batch Stochastic Bin Packing Problem in Cloud: A Chance-constrained Optimization Approach

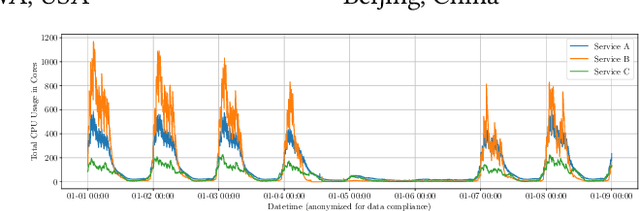
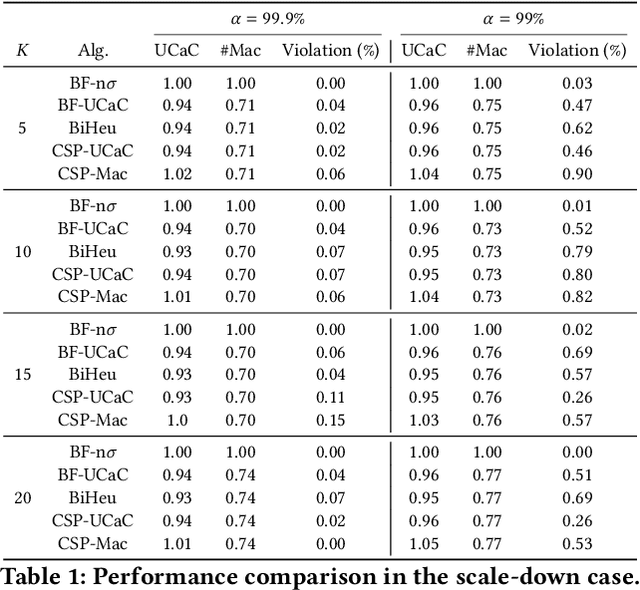
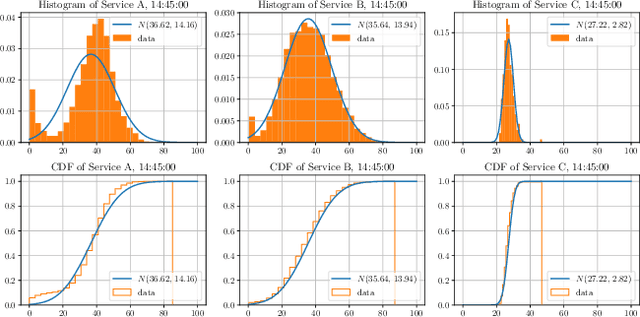
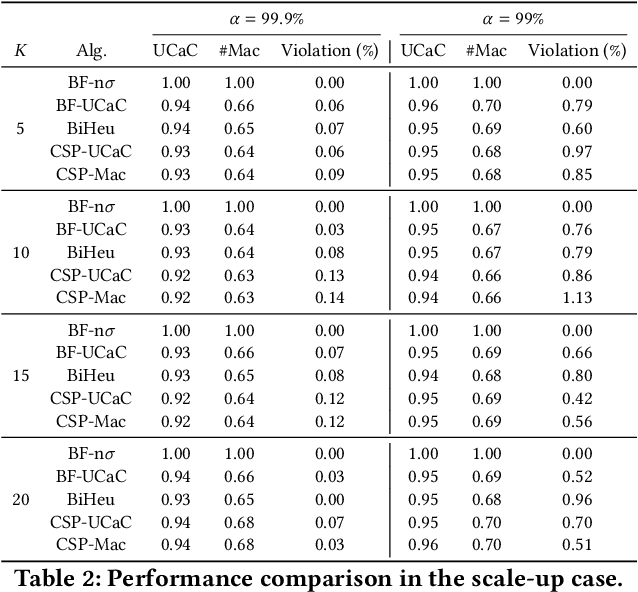
This paper investigates a critical resource allocation problem in the first party cloud: scheduling containers to machines. There are tens of services and each service runs a set of homogeneous containers with dynamic resource usage; containers of a service are scheduled daily in a batch fashion. This problem can be naturally formulated as Stochastic Bin Packing Problem (SBPP). However, traditional SBPP research often focuses on cases of empty machines, whose objective, i.e., to minimize the number of used machines, is not well-defined for the more common reality with nonempty machines. This paper aims to close this gap. First, we define a new objective metric, Used Capacity at Confidence (UCaC), which measures the maximum used resources at a probability and is proved to be consistent for both empty and nonempty machines, and reformulate the SBPP under chance constraints. Second, by modeling the container resource usage distribution in a generative approach, we reveal that UCaC can be approximated with Gaussian, which is verified by trace data of real-world applications. Third, we propose an exact solver by solving the equivalent cutting stock variant as well as two heuristics-based solvers -- UCaC best fit, bi-level heuristics. We experimentally evaluate these solvers on both synthetic datasets and real application traces, demonstrating our methodology's advantage over traditional SBPP optimal solver minimizing the number of used machines, with a low rate of resource violations.

Isomer: Transfer enhanced Dual-Channel Heterogeneous Dependency Attention Network for Aspect-based Sentiment Classification

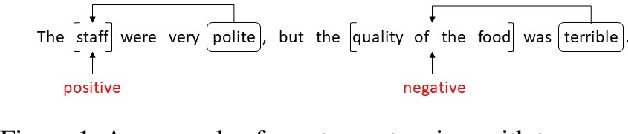
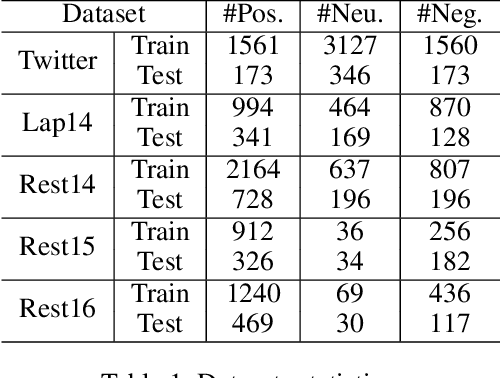
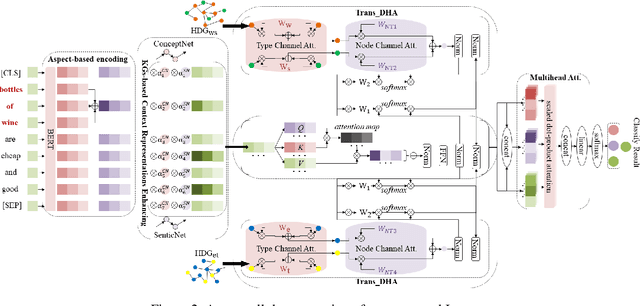
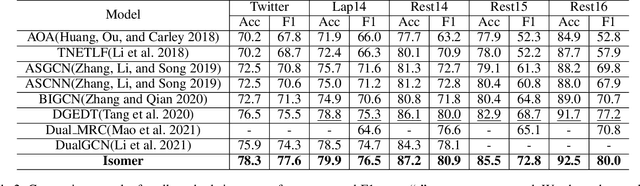
Aspect-based sentiment classification aims to predict the sentiment polarity of a specific aspect in a sentence. However, most existing methods attempt to construct dependency relations into a homogeneous dependency graph with the sparsity and ambiguity, which cannot cover the comprehensive contextualized features of short texts or consider any additional node types or semantic relation information. To solve those issues, we present a sentiment analysis model named Isomer, which performs a dual-channel attention on heterogeneous dependency graphs incorporating external knowledge, to effectively integrate other additional information. Specifically, a transfer-enhanced dual-channel heterogeneous dependency attention network is devised in Isomer to model short texts using heterogeneous dependency graphs. These heterogeneous dependency graphs not only consider different types of information but also incorporate external knowledge. Experiments studies show that our model outperforms recent models on benchmark datasets. Furthermore, the results suggest that our method captures the importance of various information features to focus on informative contextual words.

On Scalable Inference with Stochastic Gradient Descent

In many applications involving large dataset or online updating, stochastic gradient descent (SGD) provides a scalable way to compute parameter estimates and has gained increasing popularity due to its numerical convenience and memory efficiency. While the asymptotic properties of SGD-based estimators have been established decades ago, statistical inference such as interval estimation remains much unexplored. The traditional resampling method such as the bootstrap is not computationally feasible since it requires to repeatedly draw independent samples from the entire dataset. The plug-in method is not applicable when there are no explicit formulas for the covariance matrix of the estimator. In this paper, we propose a scalable inferential procedure for stochastic gradient descent, which, upon the arrival of each observation, updates the SGD estimate as well as a large number of randomly perturbed SGD estimates. The proposed method is easy to implement in practice. We establish its theoretical properties for a general class of models that includes generalized linear models and quantile regression models as special cases. The finite-sample performance and numerical utility is evaluated by simulation studies and two real data applications.

Sparse Convex Clustering

Convex clustering, a convex relaxation of k-means clustering and hierarchical clustering, has drawn recent attentions since it nicely addresses the instability issue of traditional nonconvex clustering methods. Although its computational and statistical properties have been recently studied, the performance of convex clustering has not yet been investigated in the high-dimensional clustering scenario, where the data contains a large number of features and many of them carry no information about the clustering structure. In this paper, we demonstrate that the performance of convex clustering could be distorted when the uninformative features are included in the clustering. To overcome it, we introduce a new clustering method, referred to as Sparse Convex Clustering, to simultaneously cluster observations and conduct feature selection. The key idea is to formulate convex clustering in a form of regularization, with an adaptive group-lasso penalty term on cluster centers. In order to optimally balance the tradeoff between the cluster fitting and sparsity, a tuning criterion based on clustering stability is developed. In theory, we provide an unbiased estimator for the degrees of freedom of the proposed sparse convex clustering method. Finally, the effectiveness of the sparse convex clustering is examined through a variety of numerical experiments and a real data application.

Consistent selection of tuning parameters via variable selection stability

Penalized regression models are popularly used in high-dimensional data analysis to conduct variable selection and model fitting simultaneously. Whereas success has been widely reported in literature, their performances largely depend on the tuning parameters that balance the trade-off between model fitting and model sparsity. Existing tuning criteria mainly follow the route of minimizing the estimated prediction error or maximizing the posterior model probability, such as cross-validation, AIC and BIC. This article introduces a general tuning parameter selection criterion based on a novel concept of variable selection stability. The key idea is to select the tuning parameters so that the resultant penalized regression model is stable in variable selection. The asymptotic selection consistency is established for both fixed and diverging dimensions. The effectiveness of the proposed criterion is also demonstrated in a variety of simulated examples as well as an application to the prostate cancer data.

A note on selection stability: combining stability and prediction

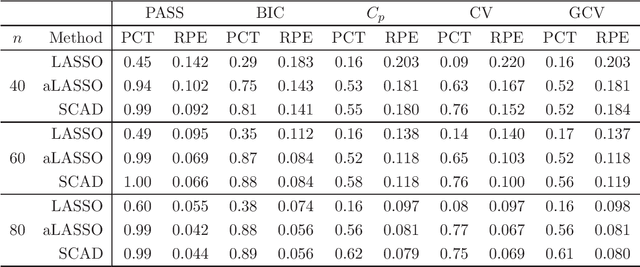
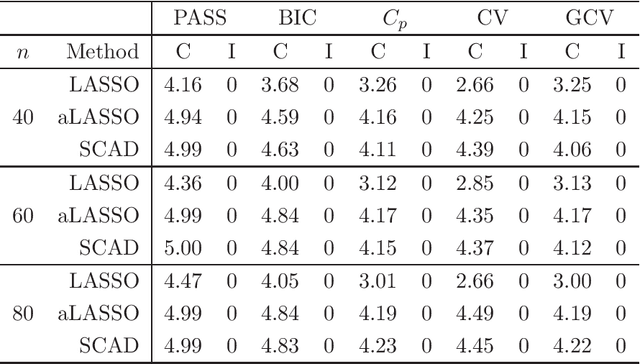
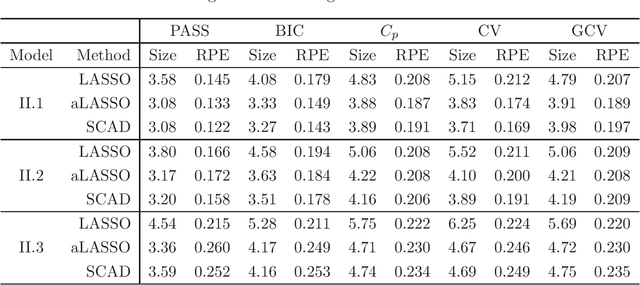
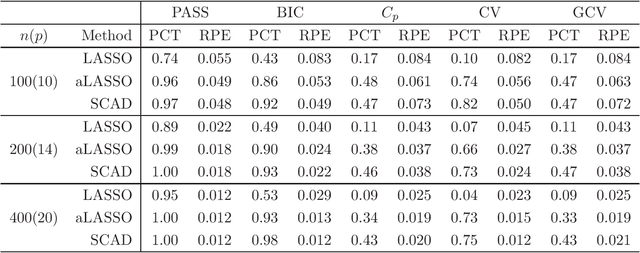
Recently, many regularized procedures have been proposed for variable selection in linear regression, but their performance depends on the tuning parameter selection. Here a criterion for the tuning parameter selection is proposed, which combines the strength of both stability selection and cross-validation and therefore is referred as the prediction and stability selection (PASS). The selection consistency is established assuming the data generating model is a subset of the full model, and the small sample performance is demonstrated through some simulation studies where the assumption is either held or violated.