Investigating the Impact of Data Selection Strategies on Language Model Performance

Data selection is critical for enhancing the performance of language models, particularly when aligning training datasets with a desired target distribution. This study explores the effects of different data selection methods and feature types on model performance. We evaluate whether selecting data subsets can influence downstream tasks, whether n-gram features improve alignment with target distributions, and whether embedding-based neural features provide complementary benefits. Through comparative experiments using baseline random selection methods and distribution aligned approaches, we provide insights into the interplay between data selection strategies and model training efficacy. All code for this study can be found on \href{https://github.com/jgu13/HIR-Hybrid-Importance-Resampling-for-Language-Models}{github repository}.

Introspective Tips: Large Language Model for In-Context Decision Making

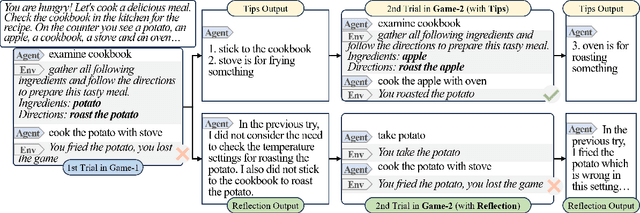
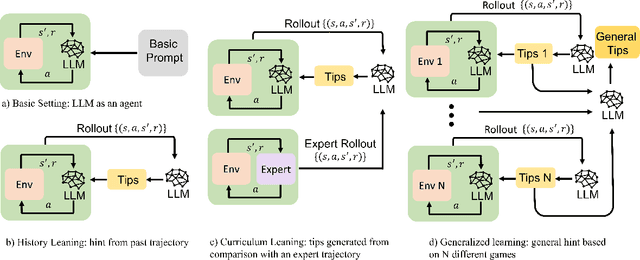
The emergence of large language models (LLMs) has substantially influenced natural language processing, demonstrating exceptional results across various tasks. In this study, we employ ``Introspective Tips" to facilitate LLMs in self-optimizing their decision-making. By introspectively examining trajectories, LLM refines its policy by generating succinct and valuable tips. Our method enhances the agent's performance in both few-shot and zero-shot learning situations by considering three essential scenarios: learning from the agent's past experiences, integrating expert demonstrations, and generalizing across diverse games. Importantly, we accomplish these improvements without fine-tuning the LLM parameters; rather, we adjust the prompt to generalize insights from the three aforementioned situations. Our framework not only supports but also emphasizes the advantage of employing LLM in in-contxt decision-making. Experiments involving over 100 games in TextWorld illustrate the superior performance of our approach.

Conservative State Value Estimation for Offline Reinforcement Learning

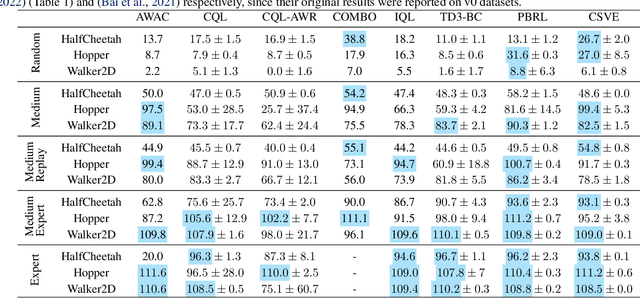
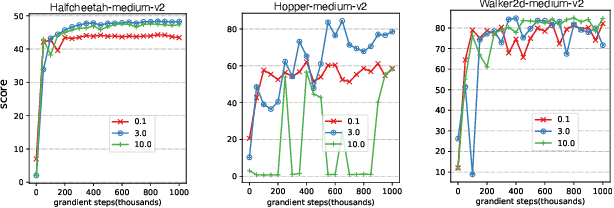
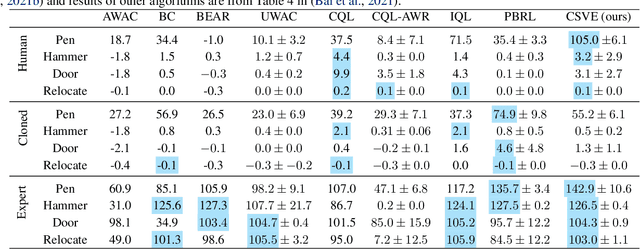
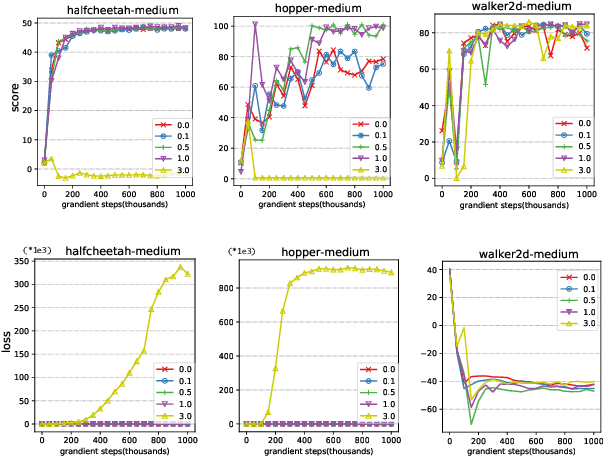
Offline reinforcement learning faces a significant challenge of value over-estimation due to the distributional drift between the dataset and the current learned policy, leading to learning failure in practice. The common approach is to incorporate a penalty term to reward or value estimation in the Bellman iterations. Meanwhile, to avoid extrapolation on out-of-distribution (OOD) states and actions, existing methods focus on conservative Q-function estimation. In this paper, we propose Conservative State Value Estimation (CSVE), a new approach that learns conservative V-function via directly imposing penalty on OOD states. Compared to prior work, CSVE allows more effective in-data policy optimization with conservative value guarantees. Further, we apply CSVE and develop a practical actor-critic algorithm in which the critic does the conservative value estimation by additionally sampling and penalizing the states \emph{around} the dataset, and the actor applies advantage weighted updates extended with state exploration to improve the policy. We evaluate in classic continual control tasks of D4RL, showing that our method performs better than the conservative Q-function learning methods and is strongly competitive among recent SOTA methods.

Solving the Batch Stochastic Bin Packing Problem in Cloud: A Chance-constrained Optimization Approach

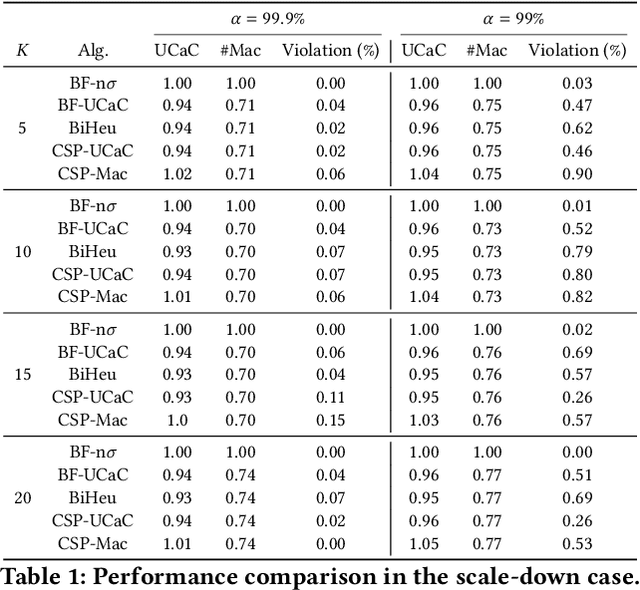
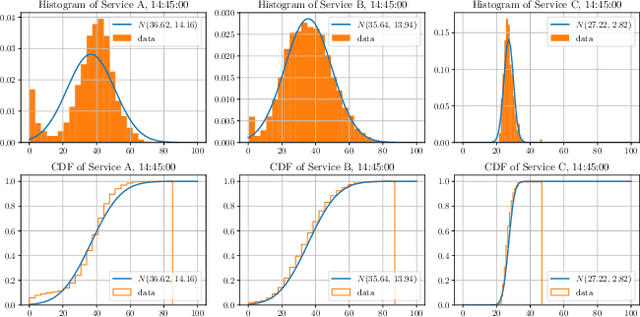
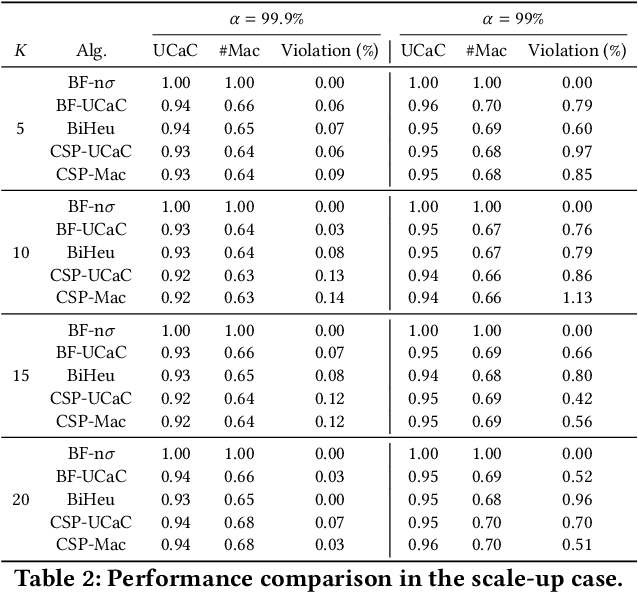
This paper investigates a critical resource allocation problem in the first party cloud: scheduling containers to machines. There are tens of services and each service runs a set of homogeneous containers with dynamic resource usage; containers of a service are scheduled daily in a batch fashion. This problem can be naturally formulated as Stochastic Bin Packing Problem (SBPP). However, traditional SBPP research often focuses on cases of empty machines, whose objective, i.e., to minimize the number of used machines, is not well-defined for the more common reality with nonempty machines. This paper aims to close this gap. First, we define a new objective metric, Used Capacity at Confidence (UCaC), which measures the maximum used resources at a probability and is proved to be consistent for both empty and nonempty machines, and reformulate the SBPP under chance constraints. Second, by modeling the container resource usage distribution in a generative approach, we reveal that UCaC can be approximated with Gaussian, which is verified by trace data of real-world applications. Third, we propose an exact solver by solving the equivalent cutting stock variant as well as two heuristics-based solvers -- UCaC best fit, bi-level heuristics. We experimentally evaluate these solvers on both synthetic datasets and real application traces, demonstrating our methodology's advantage over traditional SBPP optimal solver minimizing the number of used machines, with a low rate of resource violations.

A Surrogate Objective Framework for Prediction+Optimization with Soft Constraints

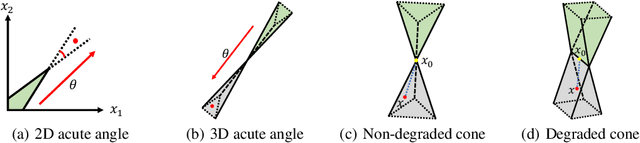
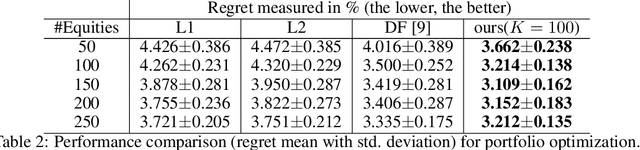
Prediction+optimization is a common real-world paradigm where we have to predict problem parameters before solving the optimization problem. However, the criteria by which the prediction model is trained are often inconsistent with the goal of the downstream optimization problem. Recently, decision-focused prediction approaches, such as SPO+ and direct optimization, have been proposed to fill this gap. However, they cannot directly handle the soft constraints with the $max$ operator required in many real-world objectives. This paper proposes a novel analytically differentiable surrogate objective framework for real-world linear and semi-definite negative quadratic programming problems with soft linear and non-negative hard constraints. This framework gives the theoretical bounds on constraints' multipliers, and derives the closed-form solution with respect to predictive parameters and thus gradients for any variable in the problem. We evaluate our method in three applications extended with soft constraints: synthetic linear programming, portfolio optimization, and resource provisioning, demonstrating that our method outperforms traditional two-staged methods and other decision-focused approaches.