Solving the Batch Stochastic Bin Packing Problem in Cloud: A Chance-constrained Optimization Approach
Paper and Code
Jul 20, 2022
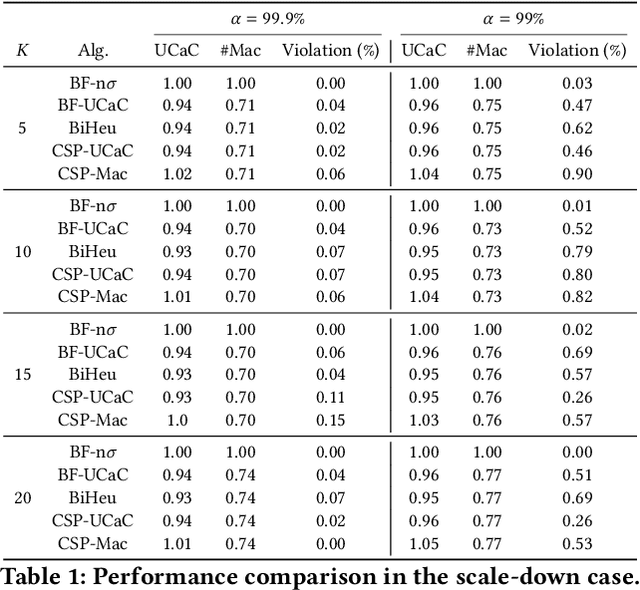
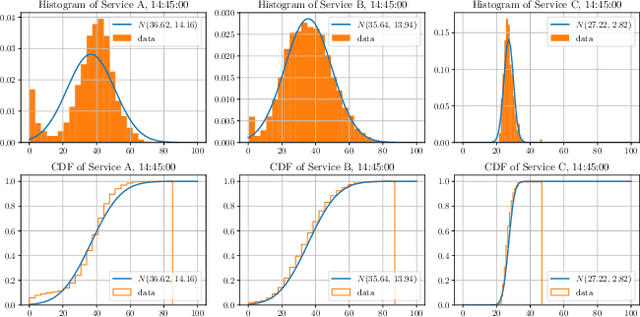
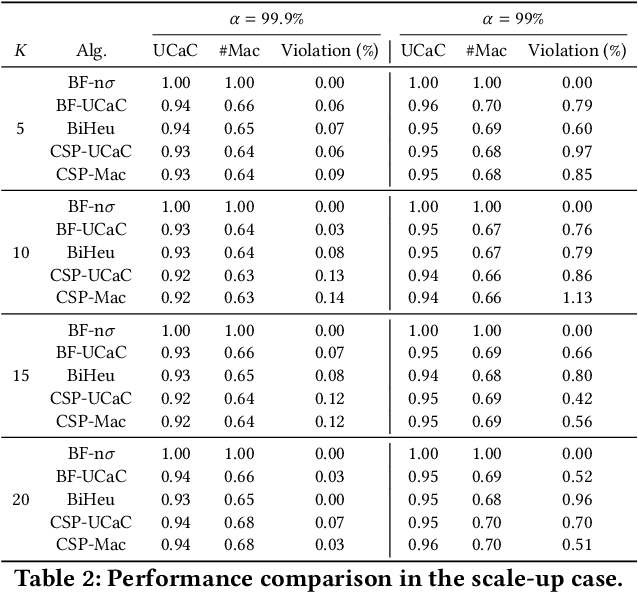
This paper investigates a critical resource allocation problem in the first party cloud: scheduling containers to machines. There are tens of services and each service runs a set of homogeneous containers with dynamic resource usage; containers of a service are scheduled daily in a batch fashion. This problem can be naturally formulated as Stochastic Bin Packing Problem (SBPP). However, traditional SBPP research often focuses on cases of empty machines, whose objective, i.e., to minimize the number of used machines, is not well-defined for the more common reality with nonempty machines. This paper aims to close this gap. First, we define a new objective metric, Used Capacity at Confidence (UCaC), which measures the maximum used resources at a probability and is proved to be consistent for both empty and nonempty machines, and reformulate the SBPP under chance constraints. Second, by modeling the container resource usage distribution in a generative approach, we reveal that UCaC can be approximated with Gaussian, which is verified by trace data of real-world applications. Third, we propose an exact solver by solving the equivalent cutting stock variant as well as two heuristics-based solvers -- UCaC best fit, bi-level heuristics. We experimentally evaluate these solvers on both synthetic datasets and real application traces, demonstrating our methodology's advantage over traditional SBPP optimal solver minimizing the number of used machines, with a low rate of resource violations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge