Junhui Wang
TopoDiffuser: A Diffusion-Based Multimodal Trajectory Prediction Model with Topometric Maps
Aug 01, 2025Abstract:This paper introduces TopoDiffuser, a diffusion-based framework for multimodal trajectory prediction that incorporates topometric maps to generate accurate, diverse, and road-compliant future motion forecasts. By embedding structural cues from topometric maps into the denoising process of a conditional diffusion model, the proposed approach enables trajectory generation that naturally adheres to road geometry without relying on explicit constraints. A multimodal conditioning encoder fuses LiDAR observations, historical motion, and route information into a unified bird's-eye-view (BEV) representation. Extensive experiments on the KITTI benchmark demonstrate that TopoDiffuser outperforms state-of-the-art methods, while maintaining strong geometric consistency. Ablation studies further validate the contribution of each input modality, as well as the impact of denoising steps and the number of trajectory samples. To support future research, we publicly release our code at https://github.com/EI-Nav/TopoDiffuser.
When Less Is More: Binary Feedback Can Outperform Ordinal Comparisons in Ranking Recovery
Jul 02, 2025Abstract:Paired comparison data, where users evaluate items in pairs, play a central role in ranking and preference learning tasks. While ordinal comparison data intuitively offer richer information than binary comparisons, this paper challenges that conventional wisdom. We propose a general parametric framework for modeling ordinal paired comparisons without ties. The model adopts a generalized additive structure, featuring a link function that quantifies the preference difference between two items and a pattern function that governs the distribution over ordinal response levels. This framework encompasses classical binary comparison models as special cases, by treating binary responses as binarized versions of ordinal data. Within this framework, we show that binarizing ordinal data can significantly improve the accuracy of ranking recovery. Specifically, we prove that under the counting algorithm, the ranking error associated with binary comparisons exhibits a faster exponential convergence rate than that of ordinal data. Furthermore, we characterize a substantial performance gap between binary and ordinal data in terms of a signal-to-noise ratio (SNR) determined by the pattern function. We identify the pattern function that minimizes the SNR and maximizes the benefit of binarization. Extensive simulations and a real application on the MovieLens dataset further corroborate our theoretical findings.
Nonparametric learning of heterogeneous graphical model on network-linked data
Jul 02, 2025Abstract:Graphical models have been popularly used for capturing conditional independence structure in multivariate data, which are often built upon independent and identically distributed observations, limiting their applicability to complex datasets such as network-linked data. This paper proposes a nonparametric graphical model that addresses these limitations by accommodating heterogeneous graph structures without imposing any specific distributional assumptions. The proposed estimation method effectively integrates network embedding with nonparametric graphical model estimation. It further transforms the graph learning task into solving a finite-dimensional linear equation system by leveraging the properties of vector-valued reproducing kernel Hilbert space. Moreover, theoretical guarantees are established for the proposed method in terms of the estimation consistency and exact recovery of the heterogeneous graph structures. Its effectiveness is also demonstrated through a variety of simulated examples and a real application to the statistician coauthorship dataset.
OpenBench: A New Benchmark and Baseline for Semantic Navigation in Smart Logistics
Feb 13, 2025
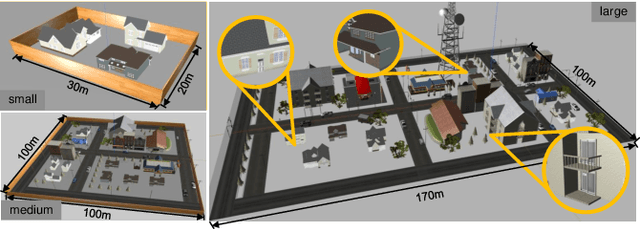


Abstract:The increasing demand for efficient last-mile delivery in smart logistics underscores the role of autonomous robots in enhancing operational efficiency and reducing costs. Traditional navigation methods, which depend on high-precision maps, are resource-intensive, while learning-based approaches often struggle with generalization in real-world scenarios. To address these challenges, this work proposes the Openstreetmap-enhanced oPen-air sEmantic Navigation (OPEN) system that combines foundation models with classic algorithms for scalable outdoor navigation. The system uses off-the-shelf OpenStreetMap (OSM) for flexible map representation, thereby eliminating the need for extensive pre-mapping efforts. It also employs Large Language Models (LLMs) to comprehend delivery instructions and Vision-Language Models (VLMs) for global localization, map updates, and house number recognition. To compensate the limitations of existing benchmarks that are inadequate for assessing last-mile delivery, this work introduces a new benchmark specifically designed for outdoor navigation in residential areas, reflecting the real-world challenges faced by autonomous delivery systems. Extensive experiments in simulated and real-world environments demonstrate the proposed system's efficacy in enhancing navigation efficiency and reliability. To facilitate further research, our code and benchmark are publicly available.
How Privacy-Savvy Are Large Language Models? A Case Study on Compliance and Privacy Technical Review
Sep 04, 2024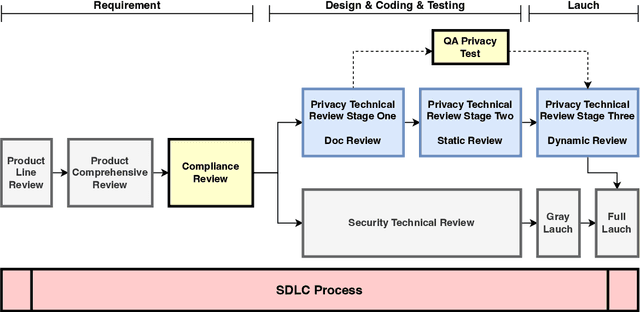
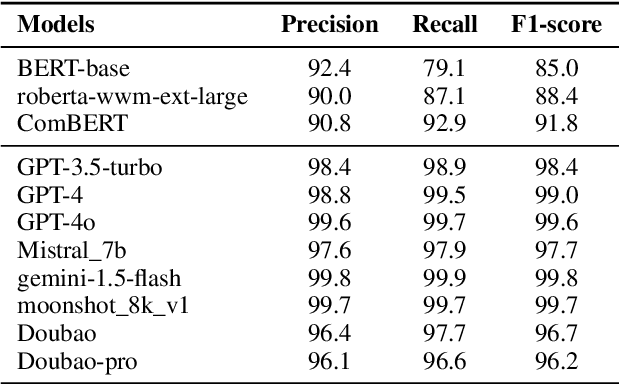
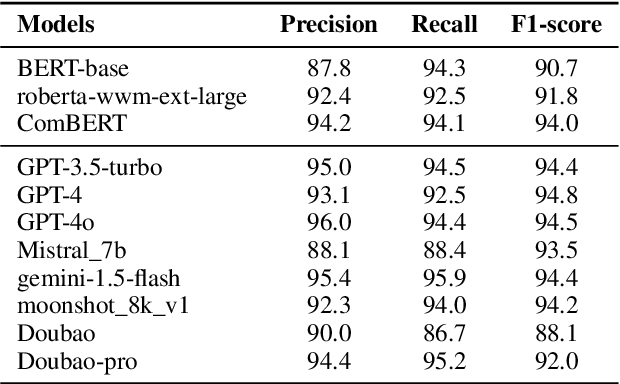
Abstract:The recent advances in large language models (LLMs) have significantly expanded their applications across various fields such as language generation, summarization, and complex question answering. However, their application to privacy compliance and technical privacy reviews remains under-explored, raising critical concerns about their ability to adhere to global privacy standards and protect sensitive user data. This paper seeks to address this gap by providing a comprehensive case study evaluating LLMs' performance in privacy-related tasks such as privacy information extraction (PIE), legal and regulatory key point detection (KPD), and question answering (QA) with respect to privacy policies and data protection regulations. We introduce a Privacy Technical Review (PTR) framework, highlighting its role in mitigating privacy risks during the software development life-cycle. Through an empirical assessment, we investigate the capacity of several prominent LLMs, including BERT, GPT-3.5, GPT-4, and custom models, in executing privacy compliance checks and technical privacy reviews. Our experiments benchmark the models across multiple dimensions, focusing on their precision, recall, and F1-scores in extracting privacy-sensitive information and detecting key regulatory compliance points. While LLMs show promise in automating privacy reviews and identifying regulatory discrepancies, significant gaps persist in their ability to fully comply with evolving legal standards. We provide actionable recommendations for enhancing LLMs' capabilities in privacy compliance, emphasizing the need for robust model improvements and better integration with legal and regulatory requirements. This study underscores the growing importance of developing privacy-aware LLMs that can both support businesses in compliance efforts and safeguard user privacy rights.
Do Large Language Models Possess Sensitive to Sentiment?
Sep 04, 2024Abstract:Large Language Models (LLMs) have recently displayed their extraordinary capabilities in language understanding. However, how to comprehensively assess the sentiment capabilities of LLMs continues to be a challenge. This paper investigates the ability of LLMs to detect and react to sentiment in text modal. As the integration of LLMs into diverse applications is on the rise, it becomes highly critical to comprehend their sensitivity to emotional tone, as it can influence the user experience and the efficacy of sentiment-driven tasks. We conduct a series of experiments to evaluate the performance of several prominent LLMs in identifying and responding appropriately to sentiments like positive, negative, and neutral emotions. The models' outputs are analyzed across various sentiment benchmarks, and their responses are compared with human evaluations. Our discoveries indicate that although LLMs show a basic sensitivity to sentiment, there are substantial variations in their accuracy and consistency, emphasizing the requirement for further enhancements in their training processes to better capture subtle emotional cues. Take an example in our findings, in some cases, the models might wrongly classify a strongly positive sentiment as neutral, or fail to recognize sarcasm or irony in the text. Such misclassifications highlight the complexity of sentiment analysis and the areas where the models need to be refined. Another aspect is that different LLMs might perform differently on the same set of data, depending on their architecture and training datasets. This variance calls for a more in-depth study of the factors that contribute to the performance differences and how they can be optimized.
Structural transfer learning of non-Gaussian DAG
Oct 16, 2023Abstract:Directed acyclic graph (DAG) has been widely employed to represent directional relationships among a set of collected nodes. Yet, the available data in one single study is often limited for accurate DAG reconstruction, whereas heterogeneous data may be collected from multiple relevant studies. It remains an open question how to pool the heterogeneous data together for better DAG structure reconstruction in the target study. In this paper, we first introduce a novel set of structural similarity measures for DAG and then present a transfer DAG learning framework by effectively leveraging information from auxiliary DAGs of different levels of similarities. Our theoretical analysis shows substantial improvement in terms of DAG reconstruction in the target study, even when no auxiliary DAG is overall similar to the target DAG, which is in sharp contrast to most existing transfer learning methods. The advantage of the proposed transfer DAG learning is also supported by extensive numerical experiments on both synthetic data and multi-site brain functional connectivity network data.
Non-Asymptotic Bounds for Adversarial Excess Risk under Misspecified Models
Sep 02, 2023Abstract:We propose a general approach to evaluating the performance of robust estimators based on adversarial losses under misspecified models. We first show that adversarial risk is equivalent to the risk induced by a distributional adversarial attack under certain smoothness conditions. This ensures that the adversarial training procedure is well-defined. To evaluate the generalization performance of the adversarial estimator, we study the adversarial excess risk. Our proposed analysis method includes investigations on both generalization error and approximation error. We then establish non-asymptotic upper bounds for the adversarial excess risk associated with Lipschitz loss functions. In addition, we apply our general results to adversarial training for classification and regression problems. For the quadratic loss in nonparametric regression, we show that the adversarial excess risk bound can be improved over those for a general loss.
Transfer learning for tensor Gaussian graphical models
Nov 17, 2022Abstract:Tensor Gaussian graphical models (GGMs), interpreting conditional independence structures within tensor data, have important applications in numerous areas. Yet, the available tensor data in one single study is often limited due to high acquisition costs. Although relevant studies can provide additional data, it remains an open question how to pool such heterogeneous data. In this paper, we propose a transfer learning framework for tensor GGMs, which takes full advantage of informative auxiliary domains even when non-informative auxiliary domains are present, benefiting from the carefully designed data-adaptive weights. Our theoretical analysis shows substantial improvement of estimation errors and variable selection consistency on the target domain under much relaxed conditions, by leveraging information from auxiliary domains. Extensive numerical experiments are conducted on both synthetic tensor graphs and a brain functional connectivity network data, which demonstrates the satisfactory performance of the proposed method.
Adaptive Embedding for Temporal Network
Nov 15, 2022
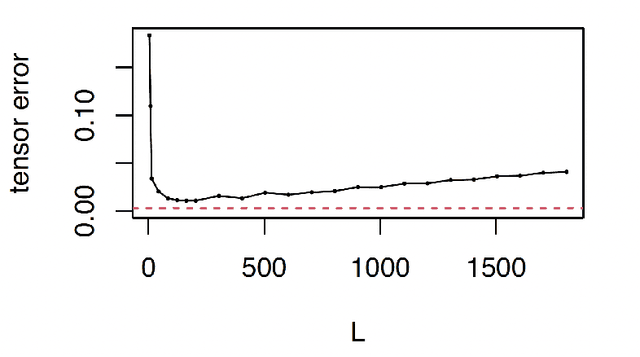
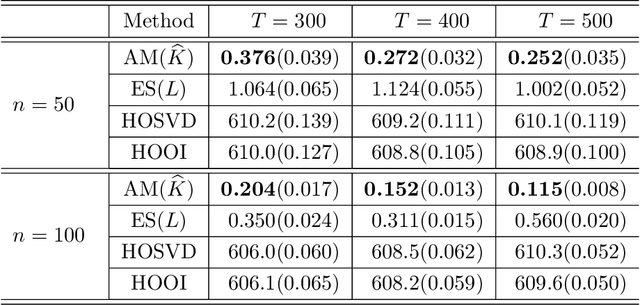
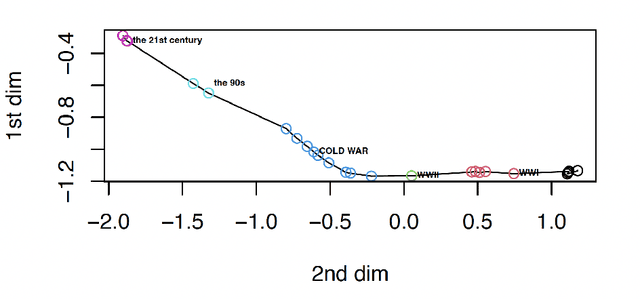
Abstract:Temporal network has become ubiquitous with the rise of online social platform and e-commerce, but largely under investigated in literature. In this paper, we propose a statistical framework for temporal network analysis, leveraging strengths of adaptive network merging, tensor decomposition and point process. A two-step embedding procedure and a regularized maximum likelihood estimate based on Poisson point process is developed, where the initial estimate is based on equal spaced time intervals while the final estimate on the adaptively merging time intervals. A projected gradient descent algorithm is proposed to facilitate estimation, where the upper bound of the tensor estimation error in each iteration is established. Through analysis, it is shown that the tensor estimation error is significantly reduced by the proposed method. Extensive numerical experiments also validate this phenomenon, as well as its advantage over other existing competitors. The proposed method is also applied to analyze a militarized interstate dispute dataset, where not only the prediction accuracy increases, but the adaptively merged intervals also lead to clear interpretation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge