360ORB-SLAM: A Visual SLAM System for Panoramic Images with Depth Completion Network

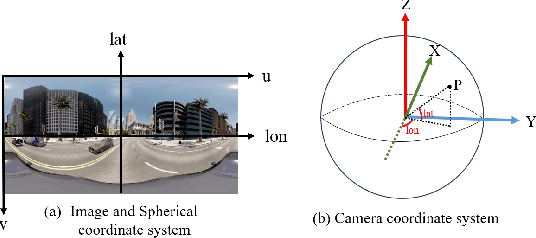
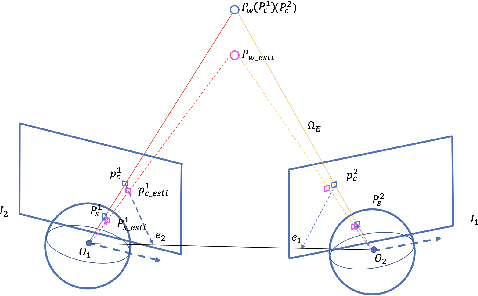
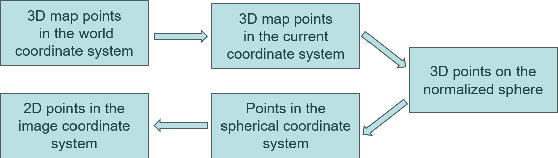
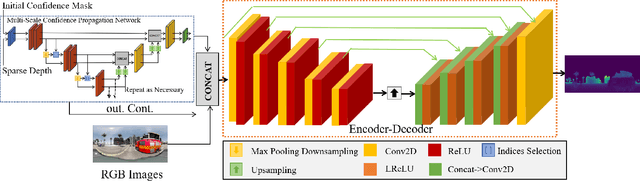
To enhance the performance and effect of AR/VR applications and visual assistance and inspection systems, visual simultaneous localization and mapping (vSLAM) is a fundamental task in computer vision and robotics. However, traditional vSLAM systems are limited by the camera's narrow field-of-view, resulting in challenges such as sparse feature distribution and lack of dense depth information. To overcome these limitations, this paper proposes a 360ORB-SLAM system for panoramic images that combines with a depth completion network. The system extracts feature points from the panoramic image, utilizes a panoramic triangulation module to generate sparse depth information, and employs a depth completion network to obtain a dense panoramic depth map. Experimental results on our novel panoramic dataset constructed based on Carla demonstrate that the proposed method achieves superior scale accuracy compared to existing monocular SLAM methods and effectively addresses the challenges of feature association and scale ambiguity. The integration of the depth completion network enhances system stability and mitigates the impact of dynamic elements on SLAM performance.

Recent Methodological Advances in Federated Learning for Healthcare

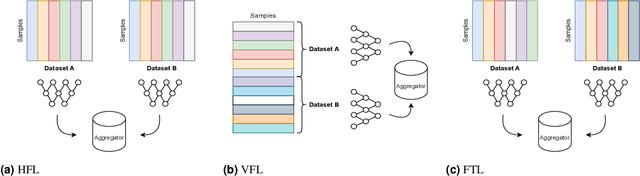
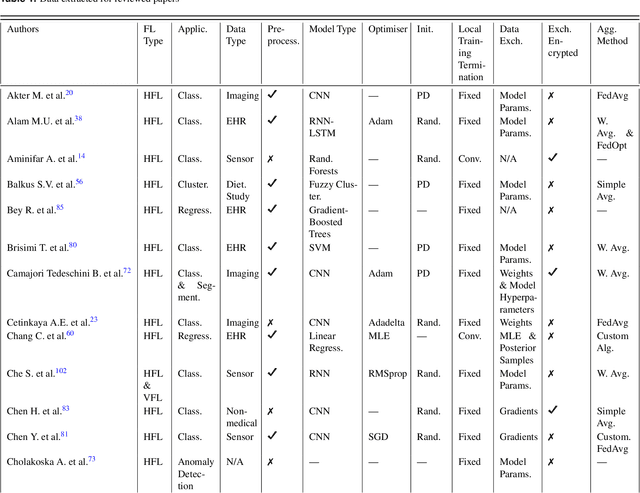
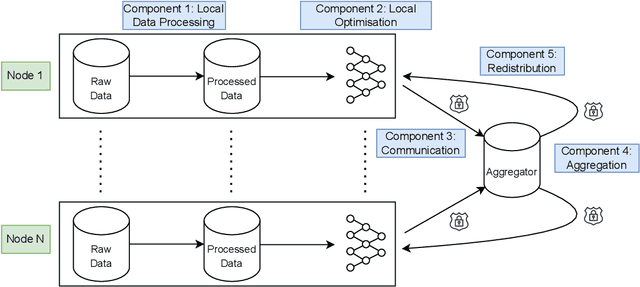
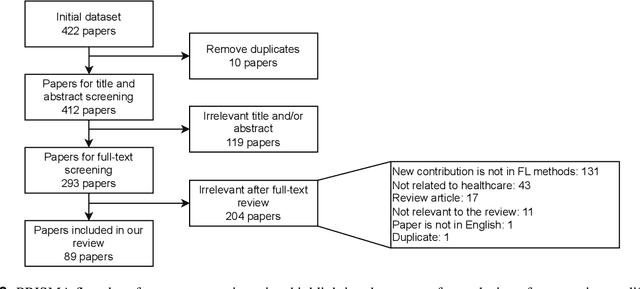
For healthcare datasets, it is often not possible to combine data samples from multiple sites due to ethical, privacy or logistical concerns. Federated learning allows for the utilisation of powerful machine learning algorithms without requiring the pooling of data. Healthcare data has many simultaneous challenges which require new methodologies to address, such as highly-siloed data, class imbalance, missing data, distribution shifts and non-standardised variables. Federated learning adds significant methodological complexity to conventional centralised machine learning, requiring distributed optimisation, communication between nodes, aggregation of models and redistribution of models. In this systematic review, we consider all papers on Scopus that were published between January 2015 and February 2023 and which describe new federated learning methodologies for addressing challenges with healthcare data. We performed a detailed review of the 89 papers which fulfilled these criteria. Significant systemic issues were identified throughout the literature which compromise the methodologies in many of the papers reviewed. We give detailed recommendations to help improve the quality of the methodology development for federated learning in healthcare.

Digital Twin Tracking Dataset : A New RGB+Depth 3D Dataset for Longer-Range Object Tracking Applications

Digital twin is a problem of augmenting real objects with their digital counterparts. It can underpin a wide range of applications in augmented reality (AR), autonomy, and UI/UX. A critical component in a good digital twin system is real-time, accurate 3D object tracking. Most existing works solve 3D object tracking through the lens of robotic grasping, employ older generations of depth sensors, and measure performance metrics that may not apply to other digital twin applications such as in AR. In this work, we create a novel RGB-D dataset, called Digital-Twin Tracking Dataset (DTTD), to enable further research of the problem and extend potential solutions towards longer ranges and mm localization accuracy. To reduce point cloud noise from the input source, we select the latest Microsoft Azure Kinect as the state-of-the-art time-of-flight (ToF) camera. In total, 103 scenes of 10 common off-the-shelf objects with rich textures are recorded, with each frame annotated with a per-pixel semantic segmentation and ground-truth object poses provided by a commercial motion capturing system. Through experiments, we demonstrate that DTTD can help researchers develop future object tracking methods and analyze new challenges. We provide the dataset, data generation, annotation, and model evaluation pipeline as open source code at: https://github.com/augcog/DTTDv1.

Scalable Bilinear $π$ Learning Using State and Action Features

Approximate linear programming (ALP) represents one of the major algorithmic families to solve large-scale Markov decision processes (MDP). In this work, we study a primal-dual formulation of the ALP, and develop a scalable, model-free algorithm called bilinear $\pi$ learning for reinforcement learning when a sampling oracle is provided. This algorithm enjoys a number of advantages. First, it adopts (bi)linear models to represent the high-dimensional value function and state-action distributions, using given state and action features. Its run-time complexity depends on the number of features, not the size of the underlying MDPs. Second, it operates in a fully online fashion without having to store any sample, thus having minimal memory footprint. Third, we prove that it is sample-efficient, solving for the optimal policy to high precision with a sample complexity linear in the dimension of the parameter space.

Lower Bound On the Computational Complexity of Discounted Markov Decision Problems

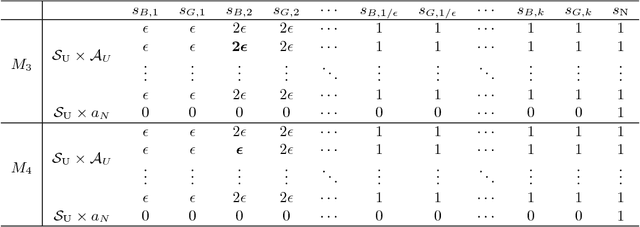
We study the computational complexity of the infinite-horizon discounted-reward Markov Decision Problem (MDP) with a finite state space $|\mathcal{S}|$ and a finite action space $|\mathcal{A}|$. We show that any randomized algorithm needs a running time at least $\Omega(|\mathcal{S}|^2|\mathcal{A}|)$ to compute an $\epsilon$-optimal policy with high probability. We consider two variants of the MDP where the input is given in specific data structures, including arrays of cumulative probabilities and binary trees of transition probabilities. For these cases, we show that the complexity lower bound reduces to $\Omega\left( \frac{|\mathcal{S}| |\mathcal{A}|}{\epsilon} \right)$. These results reveal a surprising observation that the computational complexity of the MDP depends on the data structure of input.

Stochastic Primal-Dual Methods and Sample Complexity of Reinforcement Learning

We study the online estimation of the optimal policy of a Markov decision process (MDP). We propose a class of Stochastic Primal-Dual (SPD) methods which exploit the inherent minimax duality of Bellman equations. The SPD methods update a few coordinates of the value and policy estimates as a new state transition is observed. These methods use small storage and has low computational complexity per iteration. The SPD methods find an absolute-$\epsilon$-optimal policy, with high probability, using $\mathcal{O}\left(\frac{|\mathcal{S}|^4 |\mathcal{A}|^2\sigma^2 }{(1-\gamma)^6\epsilon^2} \right)$ iterations/samples for the infinite-horizon discounted-reward MDP and $\mathcal{O}\left(\frac{|\mathcal{S}|^4 |\mathcal{A}|^2H^6\sigma^2 }{\epsilon^2} \right)$ for the finite-horizon MDP.

Random Multi-Constraint Projection: Stochastic Gradient Methods for Convex Optimization with Many Constraints

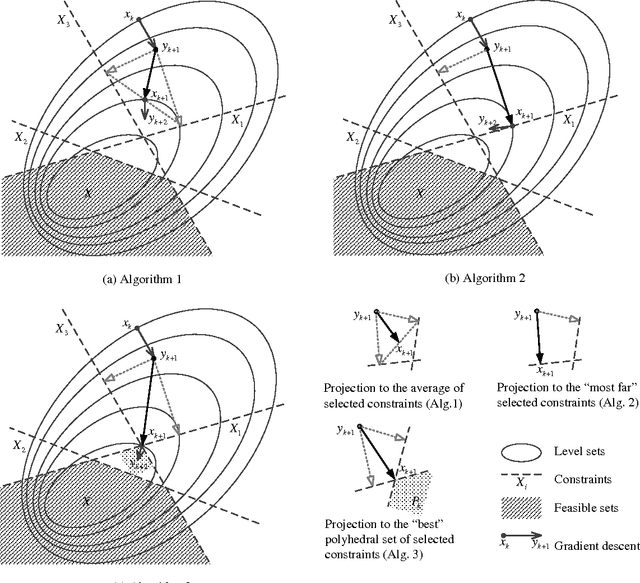
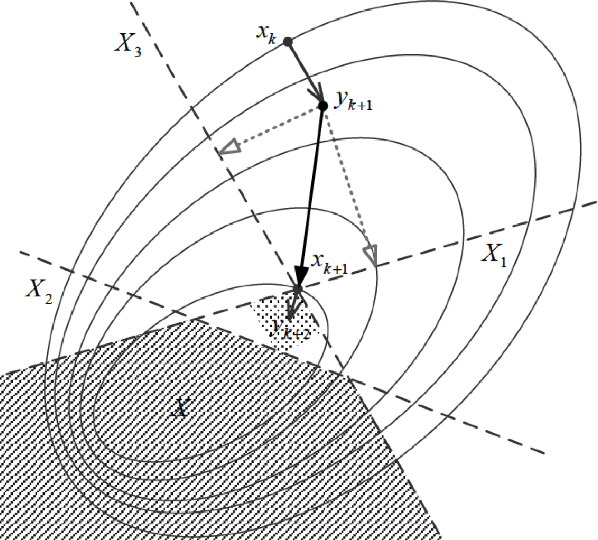
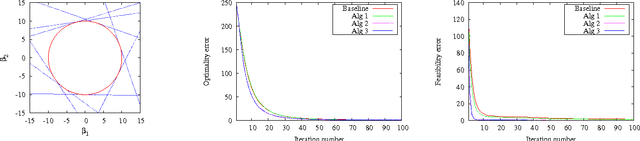
Consider convex optimization problems subject to a large number of constraints. We focus on stochastic problems in which the objective takes the form of expected values and the feasible set is the intersection of a large number of convex sets. We propose a class of algorithms that perform both stochastic gradient descent and random feasibility updates simultaneously. At every iteration, the algorithms sample a number of projection points onto a randomly selected small subsets of all constraints. Three feasibility update schemes are considered: averaging over random projected points, projecting onto the most distant sample, projecting onto a special polyhedral set constructed based on sample points. We prove the almost sure convergence of these algorithms, and analyze the iterates' feasibility error and optimality error, respectively. We provide new convergence rate benchmarks for stochastic first-order optimization with many constraints. The rate analysis and numerical experiments reveal that the algorithm using the polyhedral-set projection scheme is the most efficient one within known algorithms.