Locating the boundaries of Pareto fronts: A Many-Objective Evolutionary Algorithm Based on Corner Solution Search

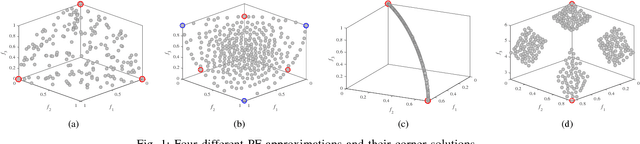
In this paper, an evolutionary many-objective optimization algorithm based on corner solution search (MaOEA-CS) was proposed. MaOEA-CS implicitly contains two phases: the exploitative search for the most important boundary optimal solutions - corner solutions, at the first phase, and the use of angle-based selection [1] with the explorative search for the extension of PF approximation at the second phase. Due to its high efficiency and robustness to the shapes of PFs, it has won the CEC'2017 Competition on Evolutionary Many-Objective Optimization. In addition, MaOEA-CS has also been applied on two real-world engineering optimization problems with very irregular PFs. The experimental results show that MaOEA-CS outperforms other six state-of-the-art compared algorithms, which indicates it has the ability to handle real-world complex optimization problems with irregular PFs.

MOEA/D with Angle-based Constrained Dominance Principle for Constrained Multi-objective Optimization Problems

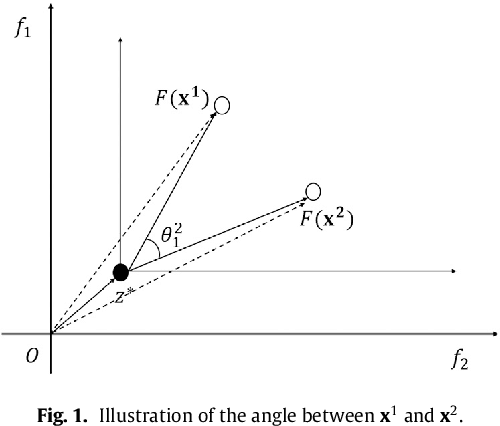
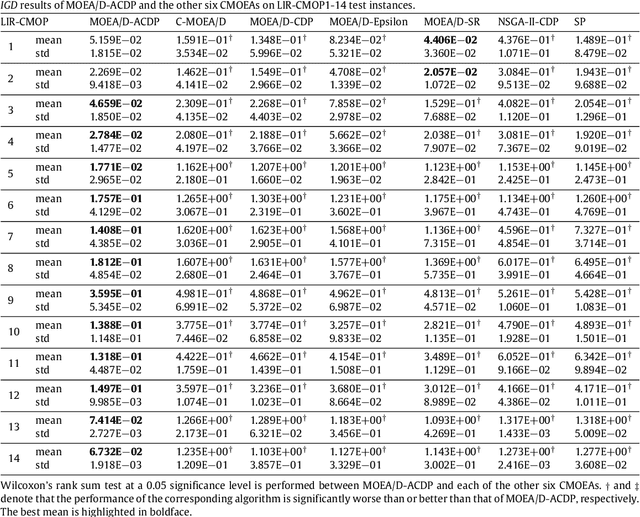
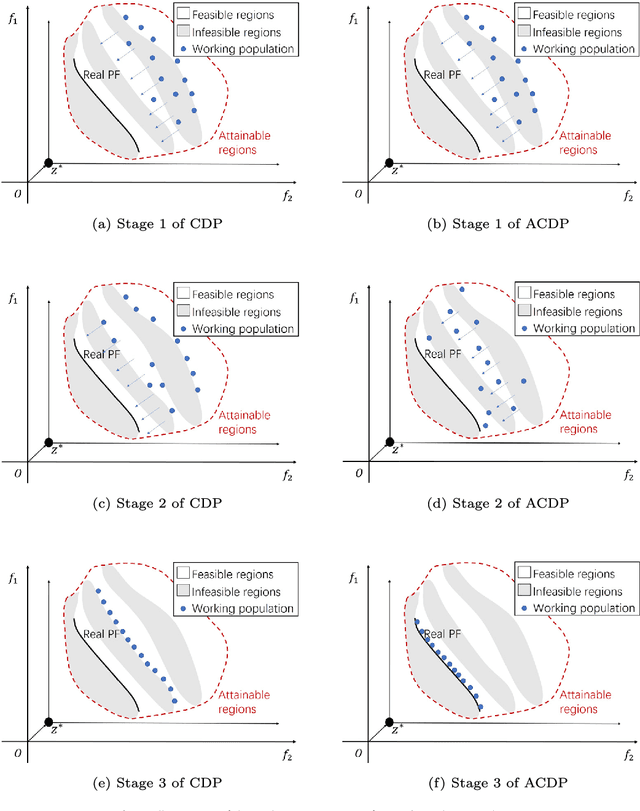
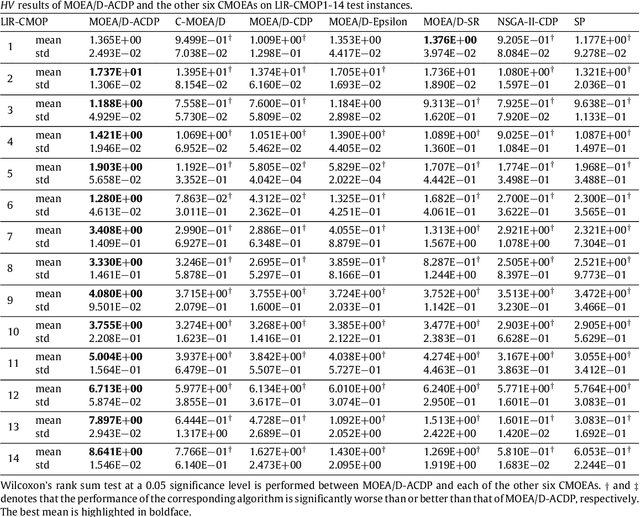
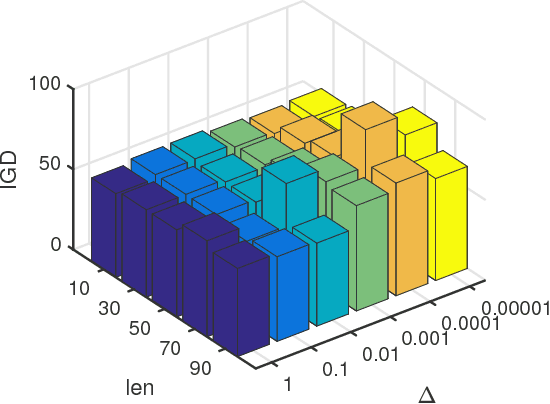
This paper proposes a novel constraint-handling mechanism named angle-based constrained dominance principle (ACDP) embedded in a decomposition-based multi-objective evolutionary algorithm (MOEA/D) to solve constrained multi-objective optimization problems (CMOPs). To maintain the diversity of the working population, ACDP utilizes the information of the angle of solutions to adjust the dominance relation of solutions during the evolutionary process. This paper uses 14 benchmark instances to evaluate the performance of the MOEA/D with ACDP (MOEA/D-ACDP). Additionally, an engineering optimization problem (which is I-beam optimization problem) is optimized. The proposed MOEA/D-ACDP, and four other decomposition-based CMOEAs, including C-MOEA/D, MOEA/D-CDP, MOEA/D-Epsilon and MOEA/D-SR are tested by the above benchmarks and the engineering application. The experimental results manifest that MOEA/D-ACDP is significantly better than the other four CMOEAs on these test instances and the real-world case, which indicates that ACDP is more effective for solving CMOPs.

A Hierarchical Image Matting Model for Blood Vessel Segmentation in Fundus images

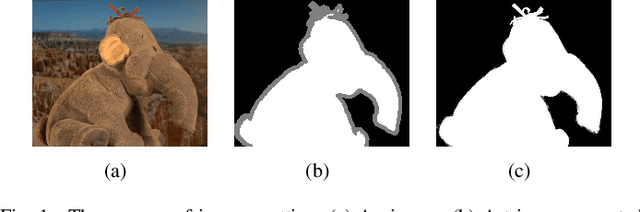
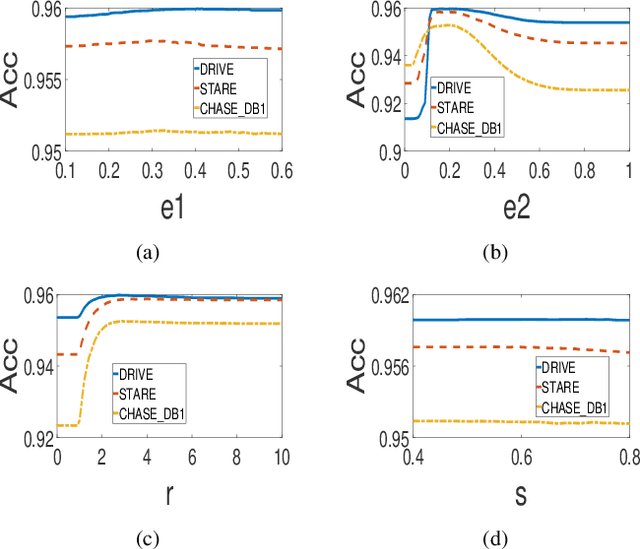
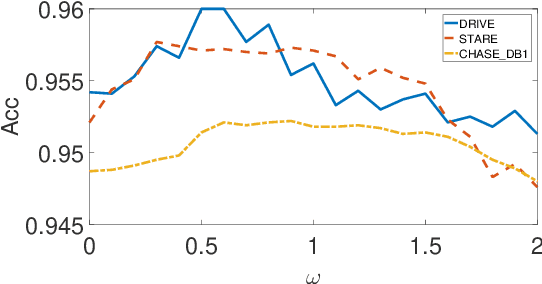
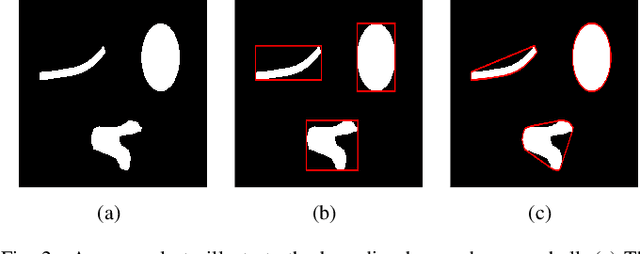
In this paper, a hierarchical image matting model is proposed to extract blood vessels from fundus images. More specifically, a hierarchical strategy utilizing the continuity and extendibility of retinal blood vessels is integrated into the image matting model for blood vessel segmentation. Normally the matting models require the user specified trimap, which separates the input image into three regions manually: the foreground, background and unknown regions. However, since creating a user specified trimap is a tedious and time-consuming task, region features of blood vessels are used to generate the trimap automatically in this paper. The proposed model has low computational complexity and outperforms many other state-ofart supervised and unsupervised methods in terms of accuracy, which achieves a vessel segmentation accuracy of 96:0%, 95:7% and 95:1% in an average time of 10:72s, 15:74s and 50:71s on images from three publicly available fundus image datasets DRIVE, STARE, and CHASE DB1, respectively.

Difficulty Adjustable and Scalable Constrained Multi-objective Test Problem Toolkit

Multi-objective evolutionary algorithms (MOEAs) have achieved great progress in recent decades, but most of them are designed to solve unconstrained multi-objective optimization problems. In fact, many real-world multi-objective problems usually contain a number of constraints. To promote the research of constrained multi-objective optimization, we first propose three primary types of difficulty, which reflect the challenges in the real-world optimization problems, to characterize the constraint functions in CMOPs, including feasibility-hardness, convergence-hardness and diversity-hardness. We then develop a general toolkit to construct difficulty adjustable and scalable constrained multi-objective optimization problems (CMOPs) with three types of parameterized constraint functions according to the proposed three primary types of difficulty. In fact, combination of the three primary constraint functions with different parameters can lead to construct a large variety of CMOPs, whose difficulty can be uniquely defined by a triplet with each of its parameter specifying the level of each primary difficulty type respectively. Furthermore, the number of objectives in this toolkit are able to scale to more than two. Based on this toolkit, we suggest nine difficulty adjustable and scalable CMOPs named DAS-CMOP1-9. To evaluate the proposed test problems, two popular CMOEAs - MOEA/D-CDP and NSGA-II-CDP are adopted to test their performances on DAS-CMOP1-9 with different difficulty triplets. The experiment results demonstrate that none of them can solve these problems efficiently, which stimulate us to develop new constrained MOEAs to solve the suggested DAS-CMOPs.

Push and Pull Search for Solving Constrained Multi-objective Optimization Problems

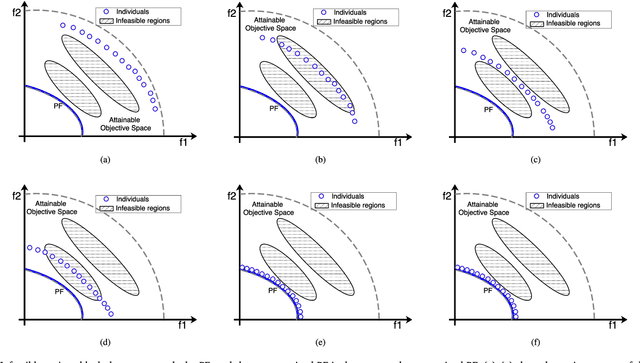
This paper proposes a push and pull search (PPS) framework for solving constrained multi-objective optimization problems (CMOPs). To be more specific, the proposed PPS divides the search process into two different stages, including the push and pull search stages. In the push stage, a multi-objective evolutionary algorithm (MOEA) is adopted to explore the search space without considering any constraints, which can help to get across infeasible regions very fast and approach the unconstrained Pareto front. Furthermore, the landscape of CMOPs with constraints can be probed and estimated in the push stage, which can be utilized to conduct the parameters setting for constraint-handling approaches applied in the pull stage. Then, a constrained multi-objective evolutionary algorithm (CMOEA) equipped with an improved epsilon constraint-handling is applied to pull the infeasible individuals achieved in the push stage to the feasible and non-dominated regions. Compared with other CMOEAs, the proposed PPS method can more efficiently get across infeasible regions and converge to the feasible and non-dominated regions by applying push and pull search strategies at different stages. To evaluate the performance regarding convergence and diversity, a set of benchmark CMOPs is used to test the proposed PPS and compare with other five CMOEAs, including MOEA/D-CDP, MOEA/D-SR, C-MOEA/D, MOEA/D-Epsilon and MOEA/D-IEpsilon. The comprehensive experimental results demonstrate that the proposed PPS achieves significantly better or competitive performance than the other five CMOEAs on most of the benchmark set.

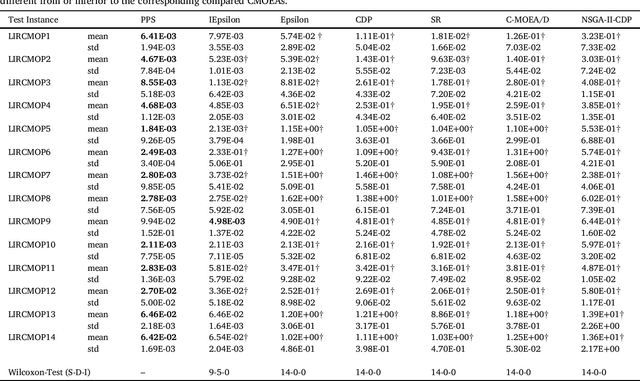
An Improved Epsilon Constraint-handling Method in MOEA/D for CMOPs with Large Infeasible Regions

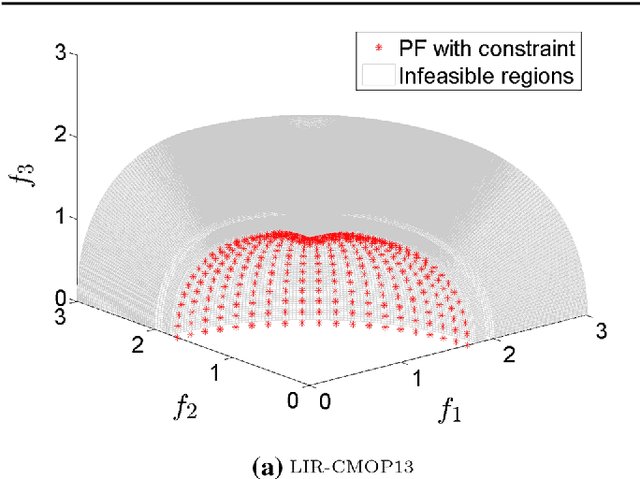
This paper proposes an improved epsilon constraint-handling mechanism, and combines it with a decomposition-based multi-objective evolutionary algorithm (MOEA/D) to solve constrained multi-objective optimization problems (CMOPs). The proposed constrained multi-objective evolutionary algorithm (CMOEA) is named MOEA/D-IEpsilon. It adjusts the epsilon level dynamically according to the ratio of feasible to total solutions (RFS) in the current population. In order to evaluate the performance of MOEA/D-IEpsilon, a new set of CMOPs with two and three objectives is designed, having large infeasible regions (relative to the feasible regions), and they are called LIR-CMOPs. Then the fourteen benchmarks, including LIR-CMOP1-14, are used to test MOEA/D-IEpsilon and four other decomposition-based CMOEAs, including MOEA/D-Epsilon, MOEA/D-SR, MOEA/D-CDP and C-MOEA/D. The experimental results indicate that MOEA/D-IEpsilon is significantly better than the other four CMOEAs on all of the test instances, which shows that MOEA/D-IEpsilon is more suitable for solving CMOPs with large infeasible regions. Furthermore, a real-world problem, namely the robot gripper optimization problem, is used to test the five CMOEAs. The experimental results demonstrate that MOEA/D-IEpsilon also outperforms the other four CMOEAs on this problem.

A New Repair Operator for Multi-objective Evolutionary Algorithm in Constrained Optimization Problems

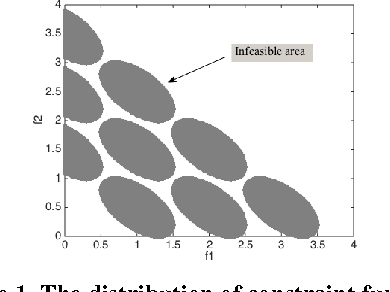
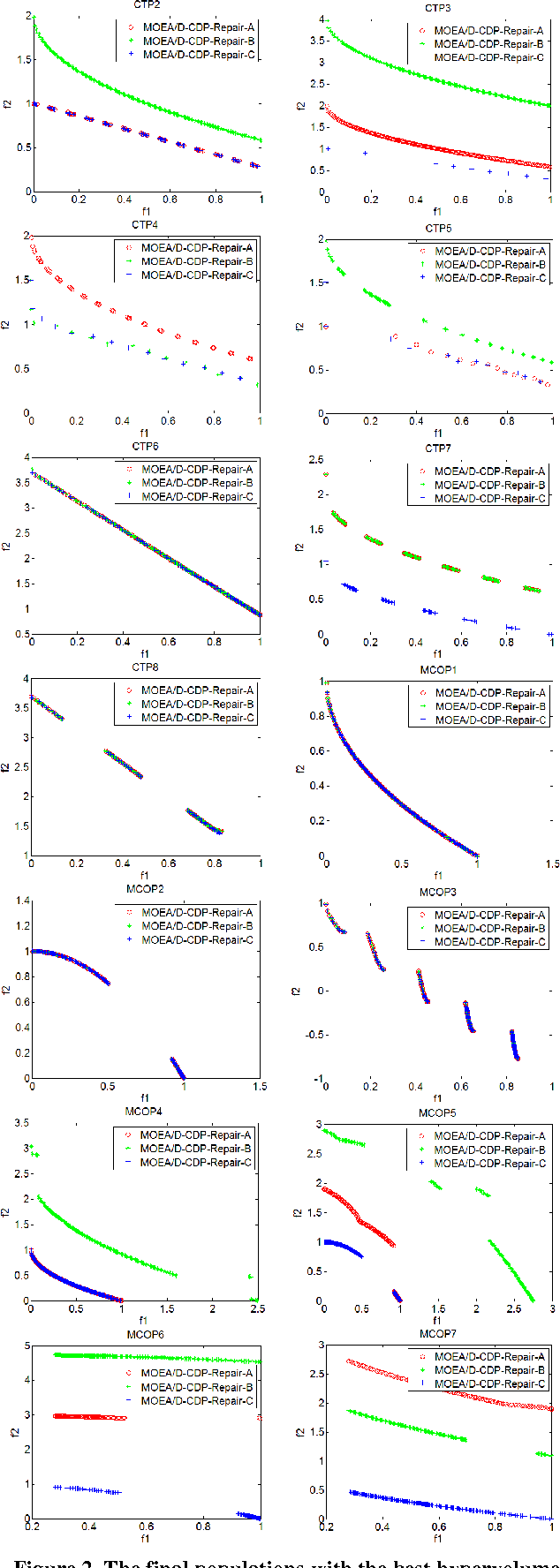
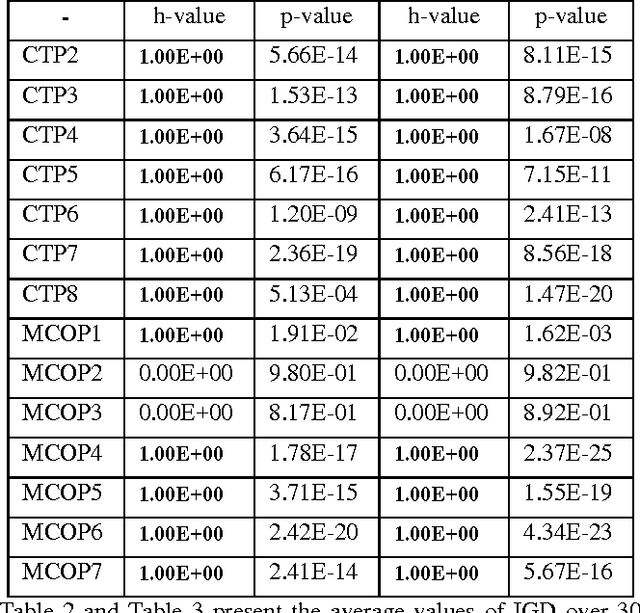
In this paper, we design a set of multi-objective constrained optimization problems (MCOPs) and propose a new repair operator to address them. The proposed repair operator is used to fix the solutions that violate the box constraints. More specifically, it employs a reversed correction strategy that can effectively avoid the population falling into local optimum. In addition, we integrate the proposed repair operator into two classical multi-objective evolutionary algorithms MOEA/D and NSGA-II. The proposed repair operator is compared with other two kinds of commonly used repair operators on benchmark problems CTPs and MCOPs. The experiment results demonstrate that our proposed approach is very effective in terms of convergence and diversity.