Push and Pull Search Embedded in an M2M Framework for Solving Constrained Multi-objective Optimization Problems

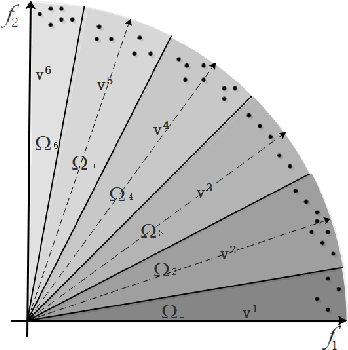
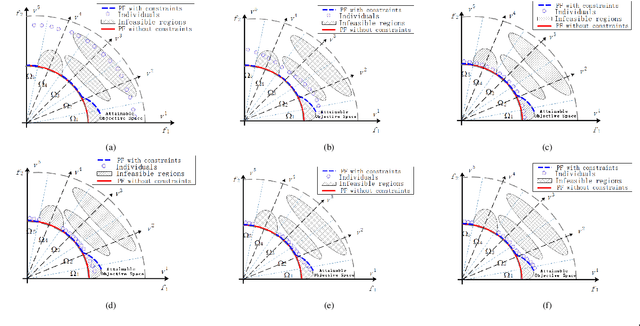
In dealing with constrained multi-objective optimization problems (CMOPs), a key issue of multi-objective evolutionary algorithms (MOEAs) is to balance the convergence and diversity of working populations.

Modeling and Multi-objective Optimization of a Kind of Teaching Manipulator

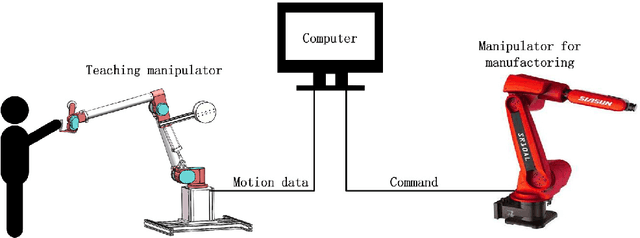
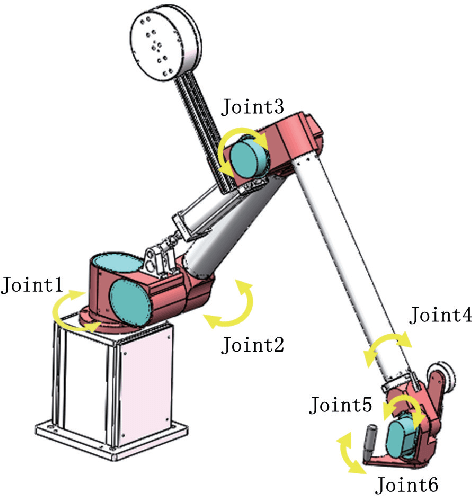
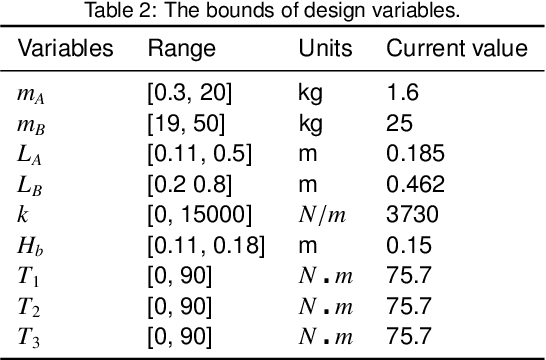
A new kind of six degree-of-freedom teaching manipulator without actuators is designed, for recording and conveniently setting a trajectory of an industrial robot. The device requires good gravity balance and operating force performance to ensure being controlled easily and fluently. In this paper, we propose a process for modeling the manipulator and then the model is used to formulate a multi-objective optimization problem to optimize the design of the testing manipulator. Three objectives, including total mass of the device, gravity balancing and operating force performance are analyzed and defined. A popular non-dominated sorting genetic algorithm (NSGA-II-CDP) is used to solve the optimization problem. The obtained solutions all outperform the design of a human expert. To extract design knowledge, an innovization study is performed to establish meaningful implicit relationship between the objective space and the decision space, which can be reused by the designer in future design process.

An Improved Epsilon Constraint-handling Method in MOEA/D for CMOPs with Large Infeasible Regions

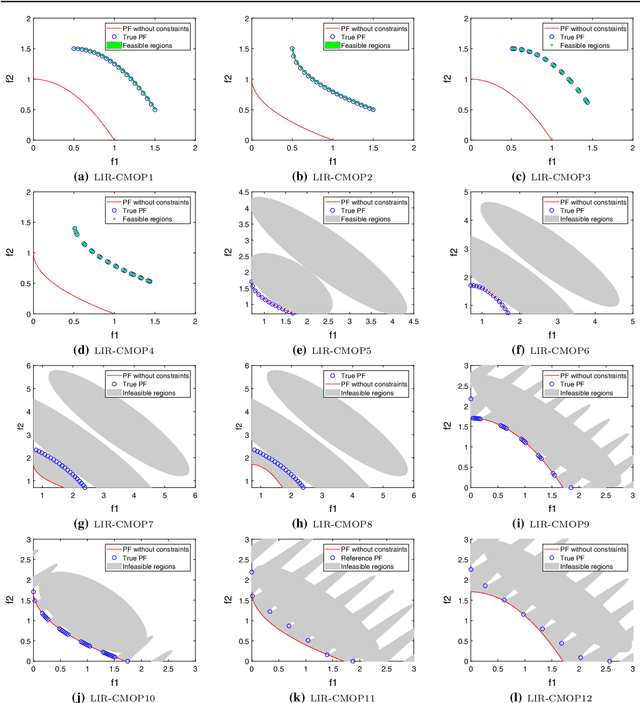
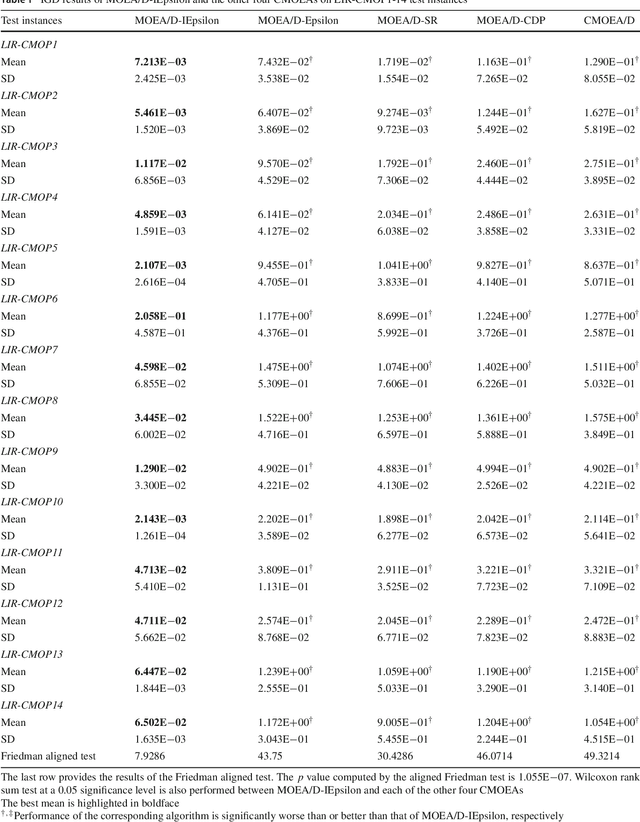
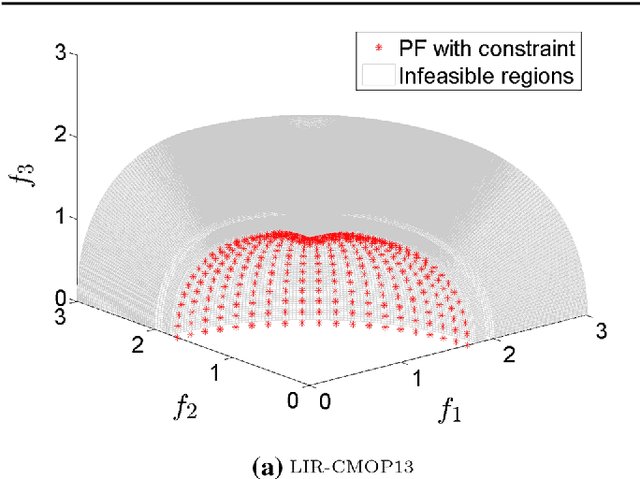
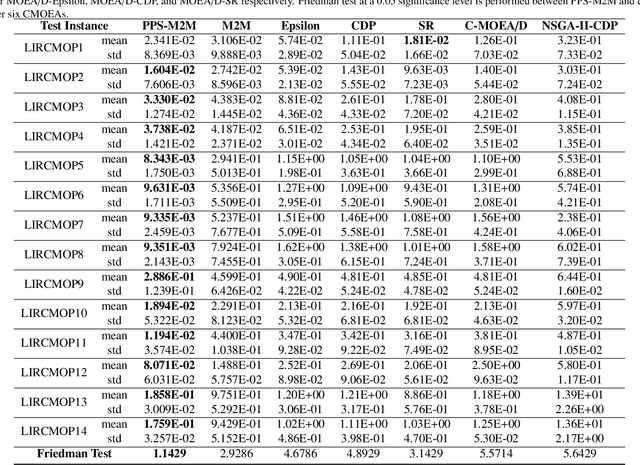
This paper proposes an improved epsilon constraint-handling mechanism, and combines it with a decomposition-based multi-objective evolutionary algorithm (MOEA/D) to solve constrained multi-objective optimization problems (CMOPs). The proposed constrained multi-objective evolutionary algorithm (CMOEA) is named MOEA/D-IEpsilon. It adjusts the epsilon level dynamically according to the ratio of feasible to total solutions (RFS) in the current population. In order to evaluate the performance of MOEA/D-IEpsilon, a new set of CMOPs with two and three objectives is designed, having large infeasible regions (relative to the feasible regions), and they are called LIR-CMOPs. Then the fourteen benchmarks, including LIR-CMOP1-14, are used to test MOEA/D-IEpsilon and four other decomposition-based CMOEAs, including MOEA/D-Epsilon, MOEA/D-SR, MOEA/D-CDP and C-MOEA/D. The experimental results indicate that MOEA/D-IEpsilon is significantly better than the other four CMOEAs on all of the test instances, which shows that MOEA/D-IEpsilon is more suitable for solving CMOPs with large infeasible regions. Furthermore, a real-world problem, namely the robot gripper optimization problem, is used to test the five CMOEAs. The experimental results demonstrate that MOEA/D-IEpsilon also outperforms the other four CMOEAs on this problem.