Automated Strabismus Detection based on Deep neural networks for Telemedicine Applications

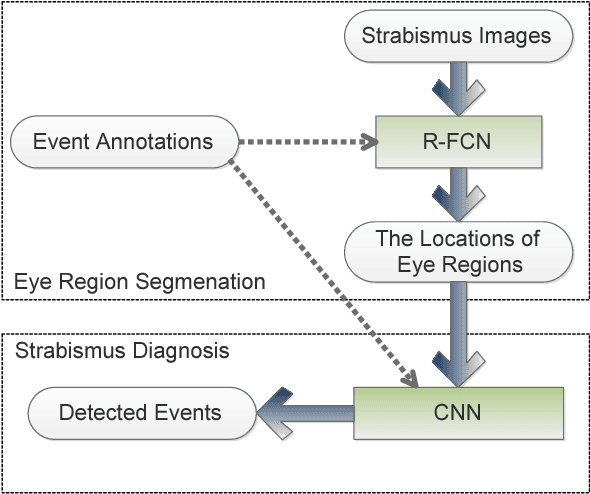
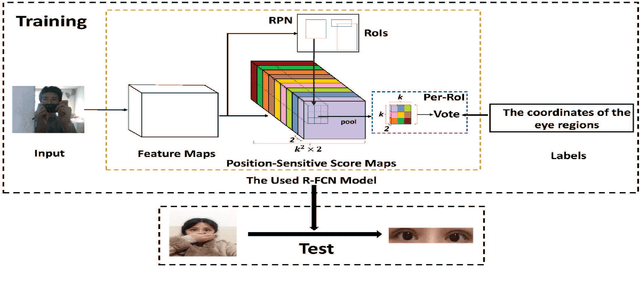
Strabismus is one of the most influential ophthalmologic diseases in humans life. Timely detection of strabismus contributes to its prognosis and treatment. Telemedicine, which has great potential to alleviate the growing demand of the diagnosis of ophthalmologic diseases, is an effective method to achieve timely strabismus detection. In addition, deep neural networks are beneficial to achieve fully automated strabismus detection. In this paper, a tele strabismus dataset is founded by the ophthalmologists. Then a new algorithm based on deep neural networks is proposed to achieve automated strabismus detection on the founded tele strabismus dataset. The proposed algorithm consists of two stages. In the first stage, R-FCN is applied to perform eye region segmentation. In the second stage, a deep convolutional neural networks is built and trained in order to classify the segmented eye regions as strabismus or normal. The experimental results on the founded tele strabismus dataset shows that the proposed method can have a good performance on automated strabismus detection for telemedicine application. Code is made publicly available at: https://github.com/jieWeiLu/Strabismus-Detection-for-Telemedicine-Application

Difficulty Adjustable and Scalable Constrained Multi-objective Test Problem Toolkit

Multi-objective evolutionary algorithms (MOEAs) have achieved great progress in recent decades, but most of them are designed to solve unconstrained multi-objective optimization problems. In fact, many real-world multi-objective problems usually contain a number of constraints. To promote the research of constrained multi-objective optimization, we first propose three primary types of difficulty, which reflect the challenges in the real-world optimization problems, to characterize the constraint functions in CMOPs, including feasibility-hardness, convergence-hardness and diversity-hardness. We then develop a general toolkit to construct difficulty adjustable and scalable constrained multi-objective optimization problems (CMOPs) with three types of parameterized constraint functions according to the proposed three primary types of difficulty. In fact, combination of the three primary constraint functions with different parameters can lead to construct a large variety of CMOPs, whose difficulty can be uniquely defined by a triplet with each of its parameter specifying the level of each primary difficulty type respectively. Furthermore, the number of objectives in this toolkit are able to scale to more than two. Based on this toolkit, we suggest nine difficulty adjustable and scalable CMOPs named DAS-CMOP1-9. To evaluate the proposed test problems, two popular CMOEAs - MOEA/D-CDP and NSGA-II-CDP are adopted to test their performances on DAS-CMOP1-9 with different difficulty triplets. The experiment results demonstrate that none of them can solve these problems efficiently, which stimulate us to develop new constrained MOEAs to solve the suggested DAS-CMOPs.

Push and Pull Search for Solving Constrained Multi-objective Optimization Problems

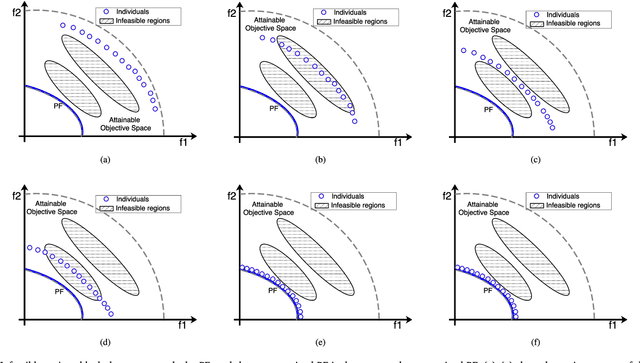
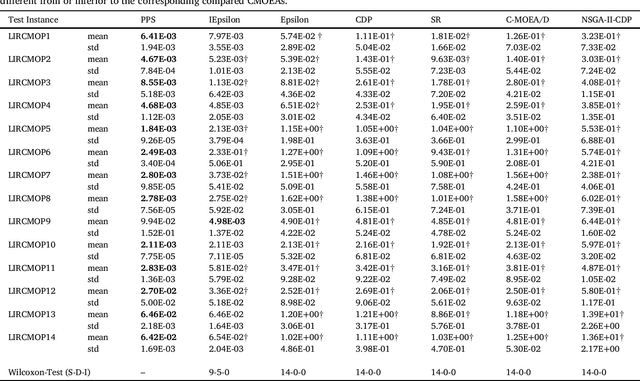
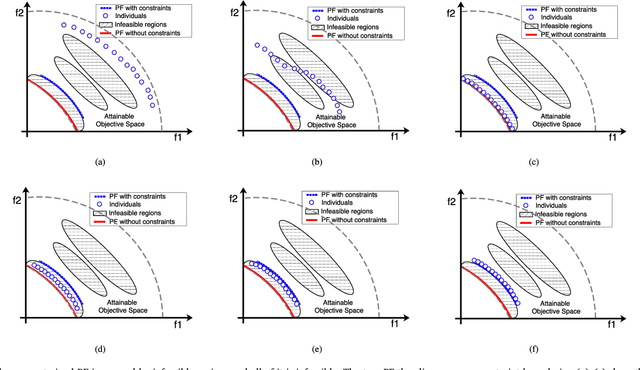
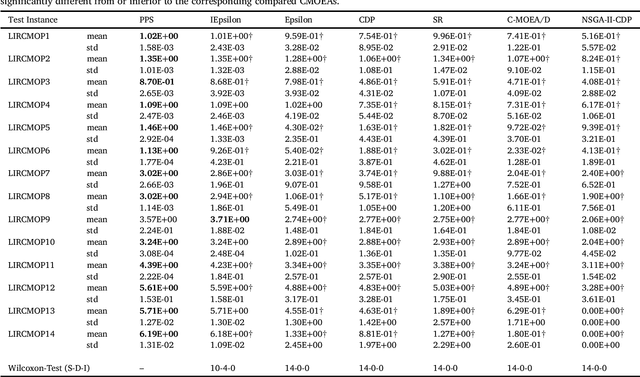
This paper proposes a push and pull search (PPS) framework for solving constrained multi-objective optimization problems (CMOPs). To be more specific, the proposed PPS divides the search process into two different stages, including the push and pull search stages. In the push stage, a multi-objective evolutionary algorithm (MOEA) is adopted to explore the search space without considering any constraints, which can help to get across infeasible regions very fast and approach the unconstrained Pareto front. Furthermore, the landscape of CMOPs with constraints can be probed and estimated in the push stage, which can be utilized to conduct the parameters setting for constraint-handling approaches applied in the pull stage. Then, a constrained multi-objective evolutionary algorithm (CMOEA) equipped with an improved epsilon constraint-handling is applied to pull the infeasible individuals achieved in the push stage to the feasible and non-dominated regions. Compared with other CMOEAs, the proposed PPS method can more efficiently get across infeasible regions and converge to the feasible and non-dominated regions by applying push and pull search strategies at different stages. To evaluate the performance regarding convergence and diversity, a set of benchmark CMOPs is used to test the proposed PPS and compare with other five CMOEAs, including MOEA/D-CDP, MOEA/D-SR, C-MOEA/D, MOEA/D-Epsilon and MOEA/D-IEpsilon. The comprehensive experimental results demonstrate that the proposed PPS achieves significantly better or competitive performance than the other five CMOEAs on most of the benchmark set.