Robust LiDAR-Camera Calibration with 2D Gaussian Splatting

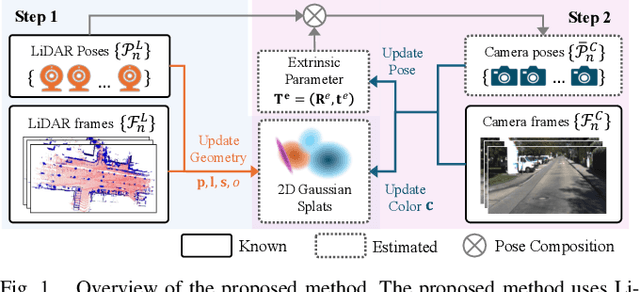
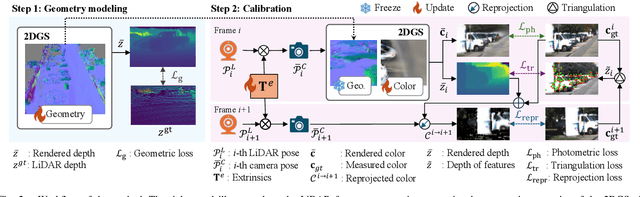
LiDAR-camera systems have become increasingly popular in robotics recently. A critical and initial step in integrating the LiDAR and camera data is the calibration of the LiDAR-camera system. Most existing calibration methods rely on auxiliary target objects, which often involve complex manual operations, whereas targetless methods have yet to achieve practical effectiveness. Recognizing that 2D Gaussian Splatting (2DGS) can reconstruct geometric information from camera image sequences, we propose a calibration method that estimates LiDAR-camera extrinsic parameters using geometric constraints. The proposed method begins by reconstructing colorless 2DGS using LiDAR point clouds. Subsequently, we update the colors of the Gaussian splats by minimizing the photometric loss. The extrinsic parameters are optimized during this process. Additionally, we address the limitations of the photometric loss by incorporating the reprojection and triangulation losses, thereby enhancing the calibration robustness and accuracy.

INF: Implicit Neural Fusion for LiDAR and Camera

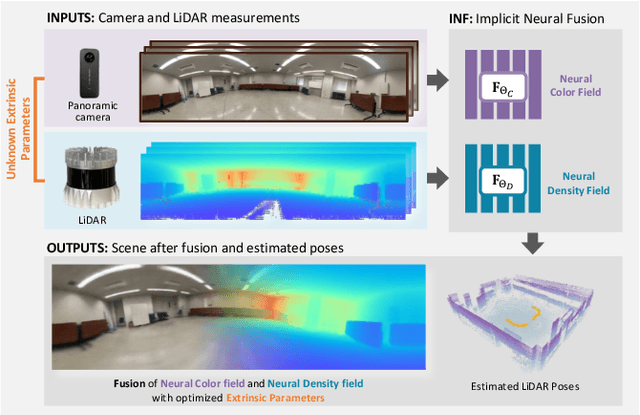
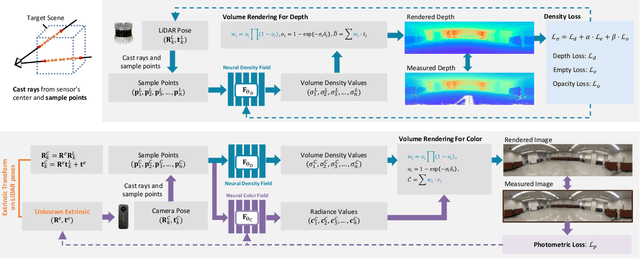
Sensor fusion has become a popular topic in robotics. However, conventional fusion methods encounter many difficulties, such as data representation differences, sensor variations, and extrinsic calibration. For example, the calibration methods used for LiDAR-camera fusion often require manual operation and auxiliary calibration targets. Implicit neural representations (INRs) have been developed for 3D scenes, and the volume density distribution involved in an INR unifies the scene information obtained by different types of sensors. Therefore, we propose implicit neural fusion (INF) for LiDAR and camera. INF first trains a neural density field of the target scene using LiDAR frames. Then, a separate neural color field is trained using camera images and the trained neural density field. Along with the training process, INF both estimates LiDAR poses and optimizes extrinsic parameters. Our experiments demonstrate the high accuracy and stable performance of the proposed method.

A New Repair Operator for Multi-objective Evolutionary Algorithm in Constrained Optimization Problems

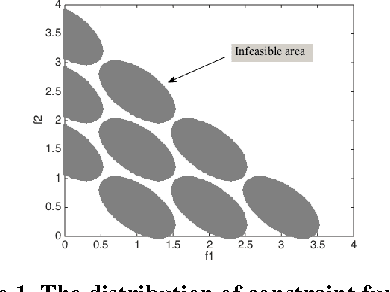
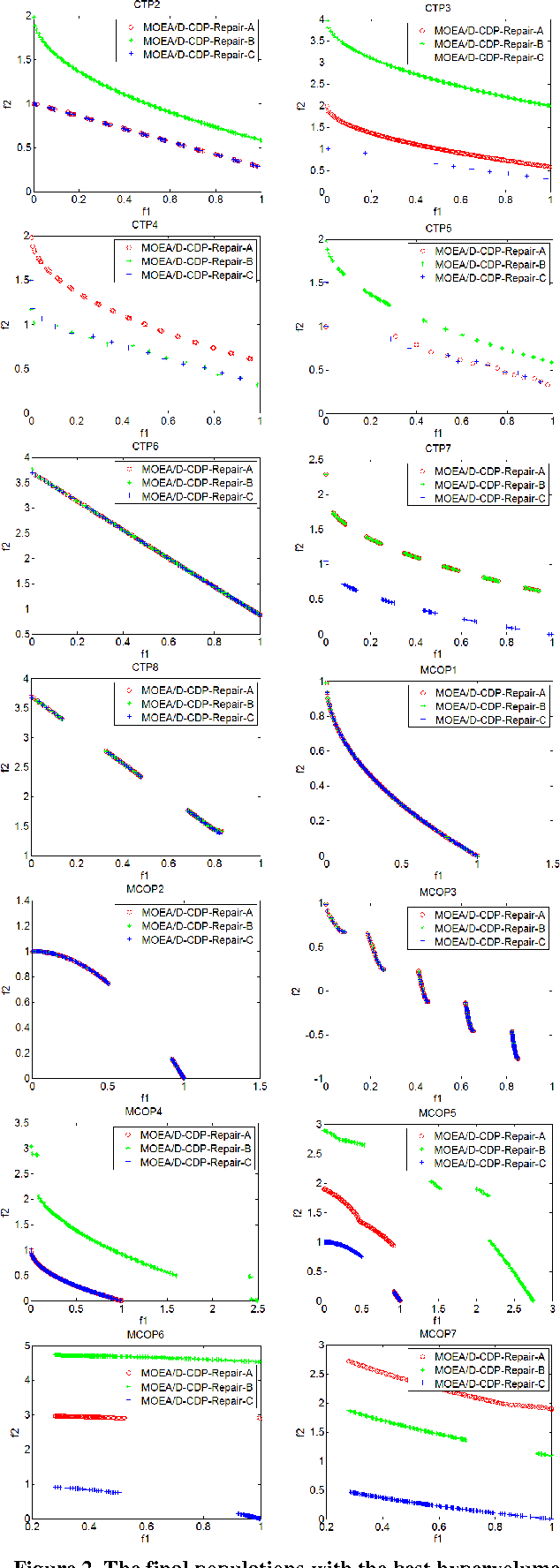
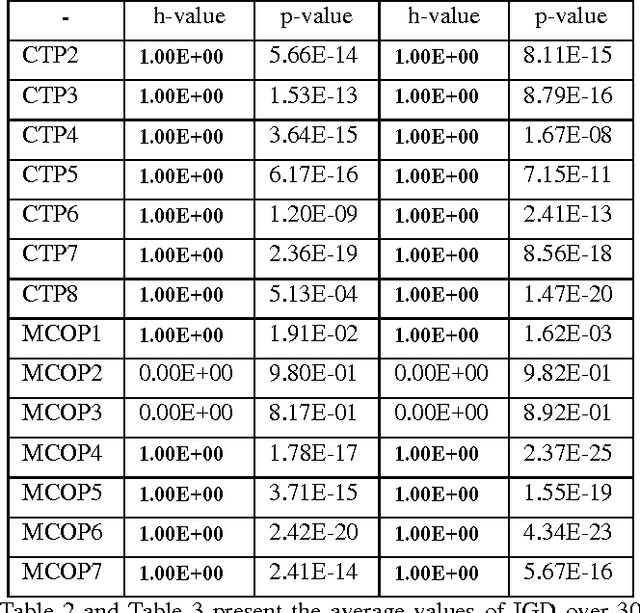
In this paper, we design a set of multi-objective constrained optimization problems (MCOPs) and propose a new repair operator to address them. The proposed repair operator is used to fix the solutions that violate the box constraints. More specifically, it employs a reversed correction strategy that can effectively avoid the population falling into local optimum. In addition, we integrate the proposed repair operator into two classical multi-objective evolutionary algorithms MOEA/D and NSGA-II. The proposed repair operator is compared with other two kinds of commonly used repair operators on benchmark problems CTPs and MCOPs. The experiment results demonstrate that our proposed approach is very effective in terms of convergence and diversity.