Wennan Zhu
Private Federated Frequency Estimation: Adapting to the Hardness of the Instance
Jun 15, 2023Abstract:In federated frequency estimation (FFE), multiple clients work together to estimate the frequencies of their collective data by communicating with a server that respects the privacy constraints of Secure Summation (SecSum), a cryptographic multi-party computation protocol that ensures that the server can only access the sum of client-held vectors. For single-round FFE, it is known that count sketching is nearly information-theoretically optimal for achieving the fundamental accuracy-communication trade-offs [Chen et al., 2022]. However, we show that under the more practical multi-round FEE setting, simple adaptations of count sketching are strictly sub-optimal, and we propose a novel hybrid sketching algorithm that is provably more accurate. We also address the following fundamental question: how should a practitioner set the sketch size in a way that adapts to the hardness of the underlying problem? We propose a two-phase approach that allows for the use of a smaller sketch size for simpler problems (e.g. near-sparse or light-tailed distributions). We conclude our work by showing how differential privacy can be added to our algorithm and verifying its superior performance through extensive experiments conducted on large-scale datasets.
Histogram Estimation under User-level Privacy with Heterogeneous Data
Jun 07, 2022



Abstract:We study the problem of histogram estimation under user-level differential privacy, where the goal is to preserve the privacy of all entries of any single user. While there is abundant literature on this classical problem under the item-level privacy setup where each user contributes only one data point, little has been known for the user-level counterpart. We consider the heterogeneous scenario where both the quantity and distribution of data can be different for each user. We propose an algorithm based on a clipping strategy that almost achieves a two-approximation with respect to the best clipping threshold in hindsight. This result holds without any distribution assumptions on the data. We also prove that the clipping bias can be significantly reduced when the counts are from non-i.i.d. Poisson distributions and show empirically that our debiasing method provides improvements even without such constraints. Experiments on both real and synthetic datasets verify our theoretical findings and demonstrate the effectiveness of our algorithms.
A Field Guide to Federated Optimization
Jul 14, 2021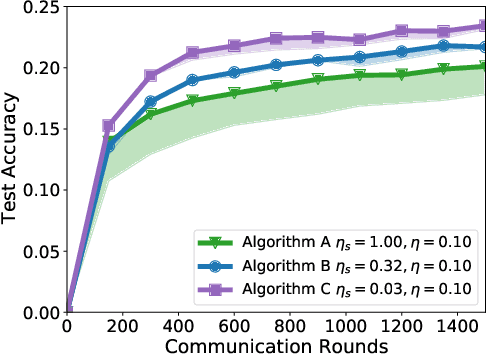


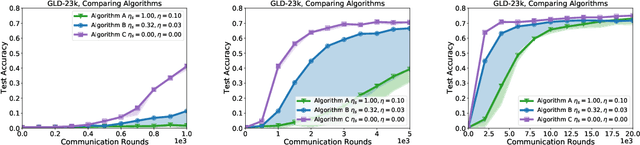
Abstract:Federated learning and analytics are a distributed approach for collaboratively learning models (or statistics) from decentralized data, motivated by and designed for privacy protection. The distributed learning process can be formulated as solving federated optimization problems, which emphasize communication efficiency, data heterogeneity, compatibility with privacy and system requirements, and other constraints that are not primary considerations in other problem settings. This paper provides recommendations and guidelines on formulating, designing, evaluating and analyzing federated optimization algorithms through concrete examples and practical implementation, with a focus on conducting effective simulations to infer real-world performance. The goal of this work is not to survey the current literature, but to inspire researchers and practitioners to design federated learning algorithms that can be used in various practical applications.
Awareness of Voter Passion Greatly Improves the Distortion of Metric Social Choice
Jun 25, 2019
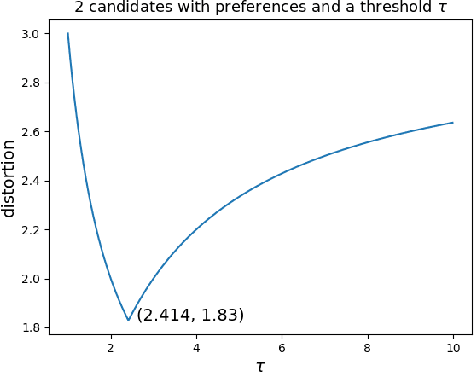
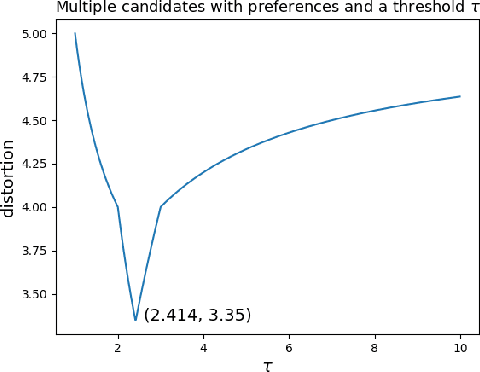

Abstract:We develop new voting mechanisms for the case when voters and candidates are located in an arbitrary unknown metric space, and the goal is to choose a candidate minimizing social cost: the total distance from the voters to this candidate. Previous work has often assumed that only ordinal preferences of the voters are known (instead of their true costs), and focused on minimizing distortion: the quality of the chosen candidate as compared with the best possible candidate. In this paper, we instead assume that a (very small) amount of information is known about the voter preference strengths, not just about their ordinal preferences. We provide mechanisms with much better distortion when this extra information is known as compared to mechanisms which use only ordinal information. We quantify tradeoffs between the amount of information known about preference strengths and the achievable distortion. We further provide advice about which type of information about preference strengths seems to be the most useful. Finally, we conclude by quantifying the ideal candidate distortion, which compares the quality of the chosen outcome with the best possible candidate that could ever exist, instead of only the best candidate that is actually in the running.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge