DeepVoting: Learning Voting Rules with Tailored Embeddings

Aggregating the preferences of multiple agents into a collective decision is a common step in many important problems across areas of computer science including information retrieval, reinforcement learning, and recommender systems. As Social Choice Theory has shown, the problem of designing algorithms for aggregation rules with specific properties (axioms) can be difficult, or provably impossible in some cases. Instead of designing algorithms by hand, one can learn aggregation rules, particularly voting rules, from data. However, the prior work in this area has required extremely large models, or been limited by the choice of preference representation, i.e., embedding. We recast the problem of designing a good voting rule into one of learning probabilistic versions of voting rules that output distributions over a set of candidates. Specifically, we use neural networks to learn probabilistic social choice functions from the literature. We show that embeddings of preference profiles derived from the social choice literature allows us to learn existing voting rules more efficiently and scale to larger populations of voters more easily than other work if the embedding is tailored to the learning objective. Moreover, we show that rules learned using embeddings can be tweaked to create novel voting rules with improved axiomatic properties. Namely, we show that existing voting rules require only minor modification to combat a probabilistic version of the No Show Paradox.

Learning Domain-Invariant Temporal Dynamics for Few-Shot Action Recognition

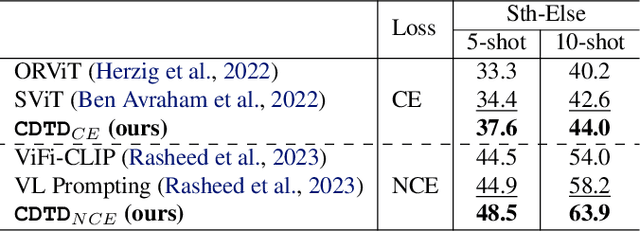
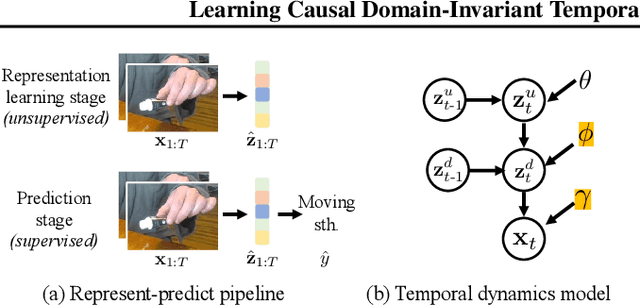
Few-shot action recognition aims at quickly adapting a pre-trained model to the novel data with a distribution shift using only a limited number of samples. Key challenges include how to identify and leverage the transferable knowledge learned by the pre-trained model. Our central hypothesis is that temporal invariance in the dynamic system between latent variables lends itself to transferability (domain-invariance). We therefore propose DITeD, or Domain-Invariant Temporal Dynamics for knowledge transfer. To detect the temporal invariance part, we propose a generative framework with a two-stage training strategy during pre-training. Specifically, we explicitly model invariant dynamics including temporal dynamic generation and transitions, and the variant visual and domain encoders. Then we pre-train the model with the self-supervised signals to learn the representation. After that, we fix the whole representation model and tune the classifier. During adaptation, we fix the transferable temporal dynamics and update the image encoder. The efficacy of our approach is revealed by the superior accuracy of DITeD over leading alternatives across standard few-shot action recognition datasets. Moreover, we validate that the learned temporal dynamic transition and temporal dynamic generation modules possess transferable qualities.

Pandering in a Flexible Representative Democracy

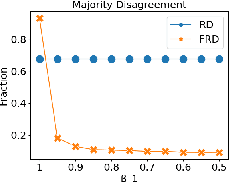
In representative democracies, the election of new representatives in regular election cycles is meant to prevent corruption and other misbehavior by elected officials and to keep them accountable in service of the ``will of the people." This democratic ideal can be undermined when candidates are dishonest when campaigning for election over these multiple cycles or rounds of voting. Much of the work on COMSOC to date has investigated strategic actions in only a single round. We introduce a novel formal model of \emph{pandering}, or strategic preference reporting by candidates seeking to be elected, and examine the resilience of two democratic voting systems to pandering within a single round and across multiple rounds. The two voting systems we compare are Representative Democracy (RD) and Flexible Representative Democracy (FRD). For each voting system, our analysis centers on the types of strategies candidates employ and how voters update their views of candidates based on how the candidates have pandered in the past. We provide theoretical results on the complexity of pandering in our setting for a single cycle, formulate our problem for multiple cycles as a Markov Decision Process, and use reinforcement learning to study the effects of pandering by both single candidates and groups of candidates across a number of rounds.

Weighting Experts with Inaccurate Judges

We consider the problem of aggregating binary votes from an ensemble of experts to reveal an underlying binary ground truth where each expert votes correctly with some independent probability. We focus on settings where the number of agents is too small for asymptotic results to apply, many experts may vote correctly with low probability, and there is no central authority who knows the experts' competences, or their probabilities of voting correctly. Our approach is to designate a second type of agent -- a judge -- to weight the experts to improve overall accuracy. The catch is that the judge has imperfect competence just like the experts. We demonstrate that having a single minimally competent judge is often better than having none at all. Using an ensemble of judges to weight the experts can provide a better weighting than any single judge; even the optimal weighting under the right conditions. As our results show, the ability of the judge(s) to distinguish between competent and incompetent experts is paramount. Lastly, given a fixed set of agents with unknown competences drawn i.i.d. from a common distribution, we show how the optimal split of the agents between judges and experts depends on the distribution.

Social Mechanism Design: A Low-Level Introduction

How do we deal with the fact that agents have preferences over both decision outcomes and the rules or procedures used to make decisions? If we create rules for aggregating preferences over rules, it would appear that we run into infinite regress with preferences and rules at successively higher "levels." The starting point of our analysis is the claim that infinite regress should not be a problem in practice, as any such preferences will necessarily be bounded in complexity and structured coherently in accordance with some (possibly latent) normative principles. Our core contributions are (1) the identification of simple, intuitive preference structures at low levels that can be generalized to form the building blocks of preferences at higher levels, and (2) the development of algorithms for maximizing the number of agents with such low-level preferences who will "accept" a decision. We analyze algorithms for acceptance maximization in two different domains: asymmetric dichotomous choice and constitutional amendment. In both settings we study the worst-case performance of the appropriate algorithms, and reveal circumstances under which universal acceptance is possible. In particular, we show that constitutional amendment procedures proposed recently by Abramowitz, Shapiro, and Talmon (2021) can achieve universal acceptance.

Towards Group Learning: Distributed Weighting of Experts

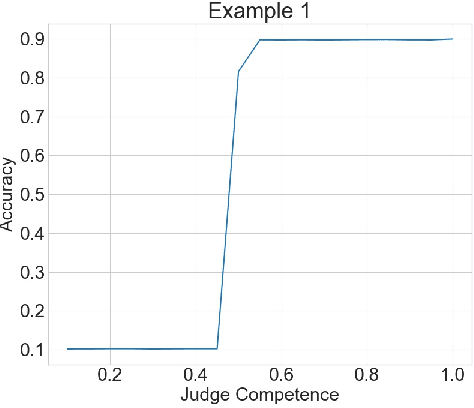
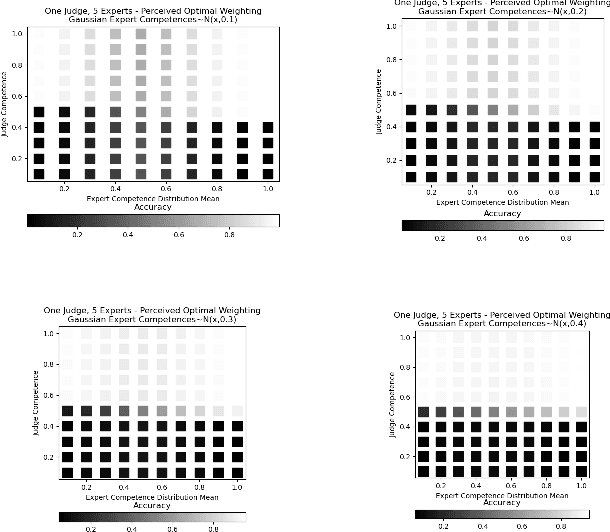
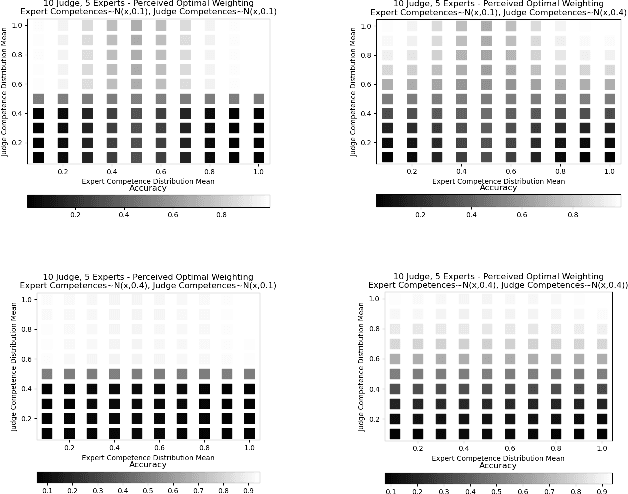
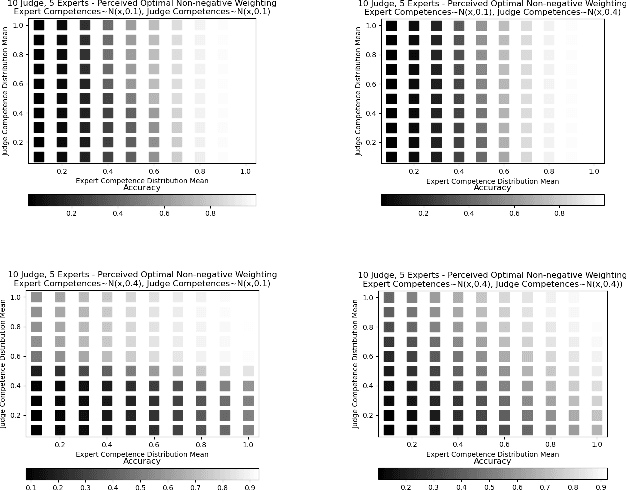
Aggregating signals from a collection of noisy sources is a fundamental problem in many domains including crowd-sourcing, multi-agent planning, sensor networks, signal processing, voting, ensemble learning, and federated learning. The core question is how to aggregate signals from multiple sources (e.g. experts) in order to reveal an underlying ground truth. While a full answer depends on the type of signal, correlation of signals, and desired output, a problem common to all of these applications is that of differentiating sources based on their quality and weighting them accordingly. It is often assumed that this differentiation and aggregation is done by a single, accurate central mechanism or agent (e.g. judge). We complicate this model in two ways. First, we investigate the setting with both a single judge, and one with multiple judges. Second, given this multi-agent interaction of judges, we investigate various constraints on the judges' reporting space. We build on known results for the optimal weighting of experts and prove that an ensemble of sub-optimal mechanisms can perform optimally under certain conditions. We then show empirically that the ensemble approximates the performance of the optimal mechanism under a broader range of conditions.

Awareness of Voter Passion Greatly Improves the Distortion of Metric Social Choice

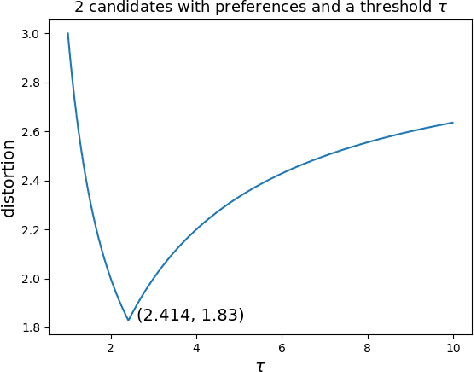
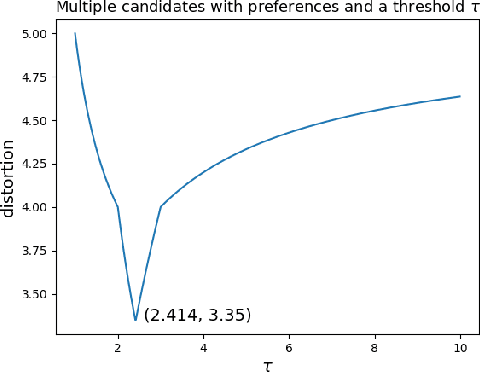
We develop new voting mechanisms for the case when voters and candidates are located in an arbitrary unknown metric space, and the goal is to choose a candidate minimizing social cost: the total distance from the voters to this candidate. Previous work has often assumed that only ordinal preferences of the voters are known (instead of their true costs), and focused on minimizing distortion: the quality of the chosen candidate as compared with the best possible candidate. In this paper, we instead assume that a (very small) amount of information is known about the voter preference strengths, not just about their ordinal preferences. We provide mechanisms with much better distortion when this extra information is known as compared to mechanisms which use only ordinal information. We quantify tradeoffs between the amount of information known about preference strengths and the achievable distortion. We further provide advice about which type of information about preference strengths seems to be the most useful. Finally, we conclude by quantifying the ideal candidate distortion, which compares the quality of the chosen outcome with the best possible candidate that could ever exist, instead of only the best candidate that is actually in the running.