Towards Group Learning: Distributed Weighting of Experts
Paper and Code
Jun 03, 2022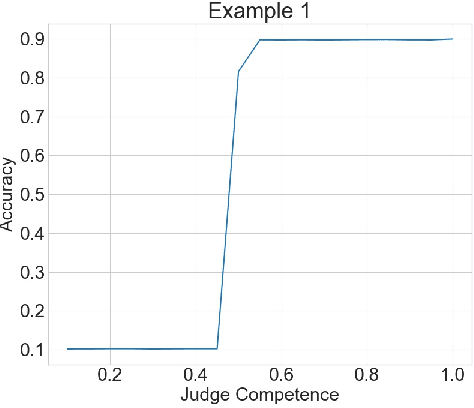
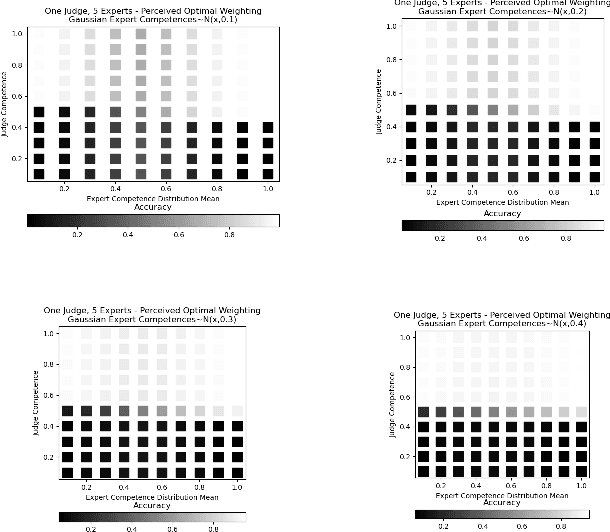
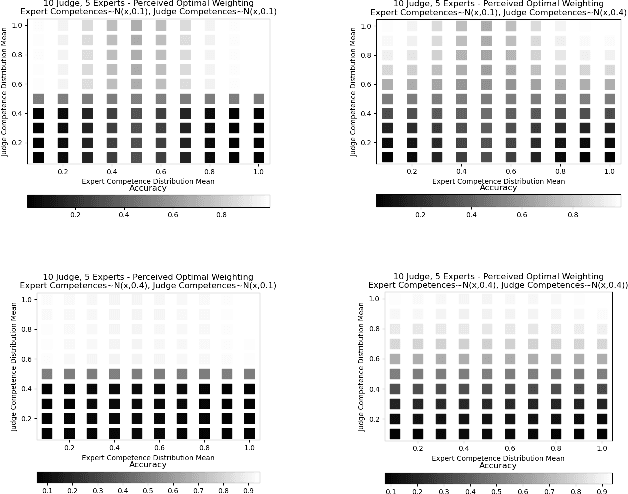
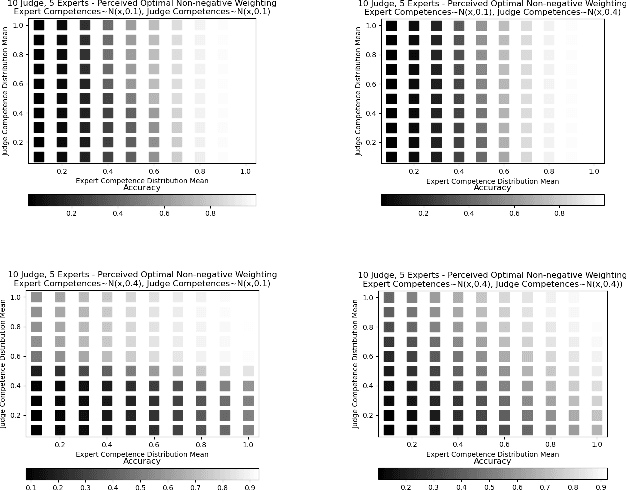
Aggregating signals from a collection of noisy sources is a fundamental problem in many domains including crowd-sourcing, multi-agent planning, sensor networks, signal processing, voting, ensemble learning, and federated learning. The core question is how to aggregate signals from multiple sources (e.g. experts) in order to reveal an underlying ground truth. While a full answer depends on the type of signal, correlation of signals, and desired output, a problem common to all of these applications is that of differentiating sources based on their quality and weighting them accordingly. It is often assumed that this differentiation and aggregation is done by a single, accurate central mechanism or agent (e.g. judge). We complicate this model in two ways. First, we investigate the setting with both a single judge, and one with multiple judges. Second, given this multi-agent interaction of judges, we investigate various constraints on the judges' reporting space. We build on known results for the optimal weighting of experts and prove that an ensemble of sub-optimal mechanisms can perform optimally under certain conditions. We then show empirically that the ensemble approximates the performance of the optimal mechanism under a broader range of conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge