HeteroMorpheus: Universal Control Based on Morphological Heterogeneity Modeling

In the field of robotic control, designing individual controllers for each robot leads to high computational costs. Universal control policies, applicable across diverse robot morphologies, promise to mitigate this challenge. Predominantly, models based on Graph Neural Networks (GNN) and Transformers are employed, owing to their effectiveness in capturing relational dynamics across a robot's limbs. However, these models typically employ homogeneous graph structures that overlook the functional diversity of different limbs. To bridge this gap, we introduce HeteroMorpheus, a novel method based on heterogeneous graph Transformer. This method uniquely addresses limb heterogeneity, fostering better representation of robot dynamics of various morphologies. Through extensive experiments we demonstrate the superiority of HeteroMorpheus against state-of-the-art methods in the capability of policy generalization, including zero-shot generalization and sample-efficient transfer to unfamiliar robot morphologies.

A Plug-and-Play Defensive Perturbation for Copyright Protection of DNN-based Applications

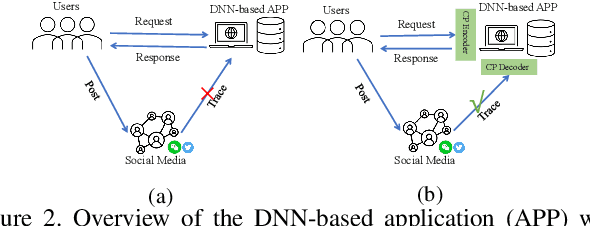
Wide deployment of deep neural networks (DNNs) based applications (e.g., style transfer, cartoonish), stimulating the requirement of copyright protection of such application's production. Although some traditional visible copyright techniques are available, they would introduce undesired traces and result in a poor user experience. In this paper, we propose a novel plug-and-play invisible copyright protection method based on defensive perturbation for DNN-based applications (i.e., style transfer). Rather than apply the perturbation to attack the DNNs model, we explore the potential utilization of perturbation in copyright protection. Specifically, we project the copyright information to the defensive perturbation with the designed copyright encoder, which is added to the image to be protected. Then, we extract the copyright information from the encoded copyrighted image with the devised copyright decoder. Furthermore, we use a robustness module to strengthen the decoding capability of the decoder toward images with various distortions (e.g., JPEG compression), which may be occurred when the user posts the image on social media. To ensure the image quality of encoded images and decoded copyright images, a loss function was elaborately devised. Objective and subjective experiment results demonstrate the effectiveness of the proposed method. We have also conducted physical world tests on social media (i.e., Wechat and Twitter) by posting encoded copyright images. The results show that the copyright information in the encoded image saved from social media can still be correctly extracted.

RecFNO: a resolution-invariant flow and heat field reconstruction method from sparse observations via Fourier neural operator

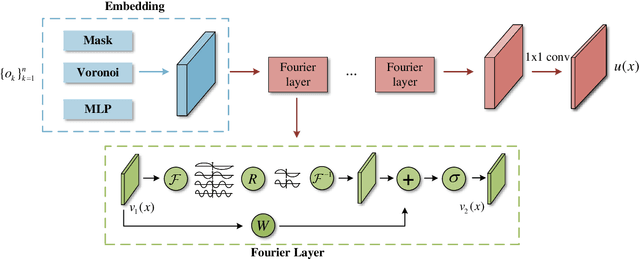
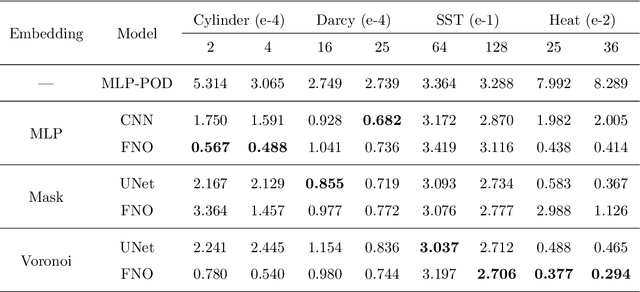
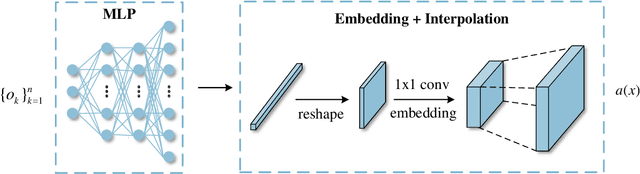
Perception of the full state is an essential technology to support the monitoring, analysis, and design of physical systems, one of whose challenges is to recover global field from sparse observations. Well-known for brilliant approximation ability, deep neural networks have been attractive to data-driven flow and heat field reconstruction studies. However, limited by network structure, existing researches mostly learn the reconstruction mapping in finite-dimensional space and has poor transferability to variable resolution of outputs. In this paper, we extend the new paradigm of neural operator and propose an end-to-end physical field reconstruction method with both excellent performance and mesh transferability named RecFNO. The proposed method aims to learn the mapping from sparse observations to flow and heat field in infinite-dimensional space, contributing to a more powerful nonlinear fitting capacity and resolution-invariant characteristic. Firstly, according to different usage scenarios, we develop three types of embeddings to model the sparse observation inputs: MLP, mask, and Voronoi embedding. The MLP embedding is propitious to more sparse input, while the others benefit from spatial information preservation and perform better with the increase of observation data. Then, we adopt stacked Fourier layers to reconstruct physical field in Fourier space that regularizes the overall recovered field by Fourier modes superposition. Benefiting from the operator in infinite-dimensional space, the proposed method obtains remarkable accuracy and better resolution transferability among meshes. The experiments conducted on fluid mechanics and thermology problems show that the proposed method outperforms existing POD-based and CNN-based methods in most cases and has the capacity to achieve zero-shot super-resolution.

Multi-fidelity surrogate modeling for temperature field prediction using deep convolution neural network

Temperature field prediction is of great importance in the thermal design of systems engineering, and building the surrogate model is an effective way for the task. Generally, large amounts of labeled data are required to guarantee a good prediction performance of the surrogate model, especially the deep learning model, which have more parameters and better representational ability. However, labeled data, especially high-fidelity labeled data, are usually expensive to obtain and sometimes even impossible. To solve this problem, this paper proposes a pithy deep multi-fidelity model (DMFM) for temperature field prediction, which takes advantage of low-fidelity data to boost the performance with less high-fidelity data. First, a pre-train and fine-tune paradigm are developed in DMFM to train the low-fidelity and high-fidelity data, which significantly reduces the complexity of the deep surrogate model. Then, a self-supervised learning method for training the physics-driven deep multi-fidelity model (PD-DMFM) is proposed, which fully utilizes the physics characteristics of the engineering systems and reduces the dependence on large amounts of labeled low-fidelity data in the training process. Two diverse temperature field prediction problems are constructed to validate the effectiveness of DMFM and PD-DMFM, and the result shows that the proposed method can greatly reduce the dependence of the model on high-fidelity data.

Robust Regression with Highly Corrupted Data via Physics Informed Neural Networks

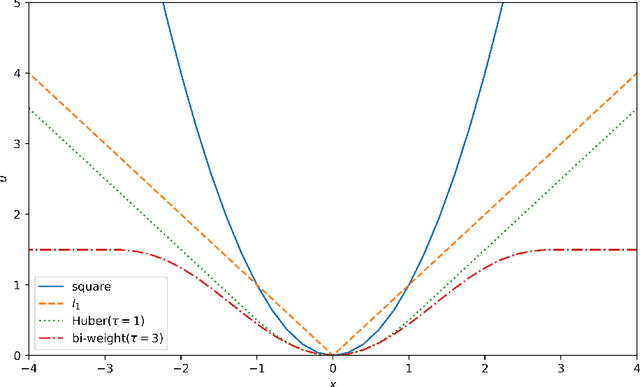
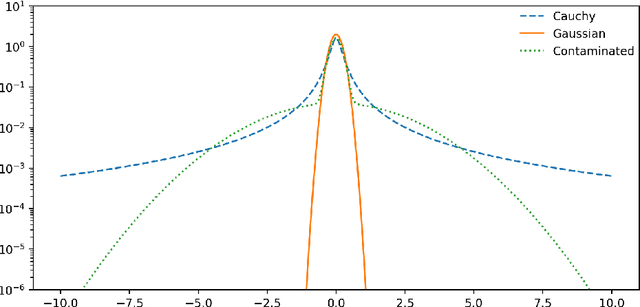
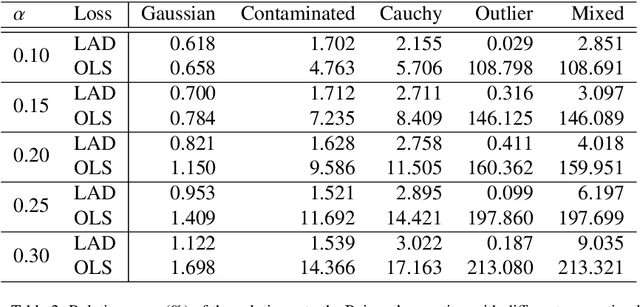
Physics-informed neural networks (PINNs) have been proposed to solve two main classes of problems: data-driven solutions and data-driven discovery of partial differential equations. This task becomes prohibitive when such data is highly corrupted due to the possible sensor mechanism failing. We propose the Least Absolute Deviation based PINN (LAD-PINN) to reconstruct the solution and recover unknown parameters in PDEs - even if spurious data or outliers corrupt a large percentage of the observations. To further improve the accuracy of recovering hidden physics, the two-stage Median Absolute Deviation based PINN (MAD-PINN) is proposed, where LAD-PINN is employed as an outlier detector followed by MAD screening out the highly corrupted data. Then the vanilla PINN or its variants can be subsequently applied to exploit the remaining normal data. Through several examples, including Poisson's equation, wave equation, and steady or unsteady Navier-Stokes equations, we illustrate the generalizability, accuracy and efficiency of the proposed algorithms for recovering governing equations from noisy and highly corrupted measurement data.

Heat Source Layout Optimization Using Automatic Deep Learning Surrogate Model and Multimodal Neighborhood Search Algorithm

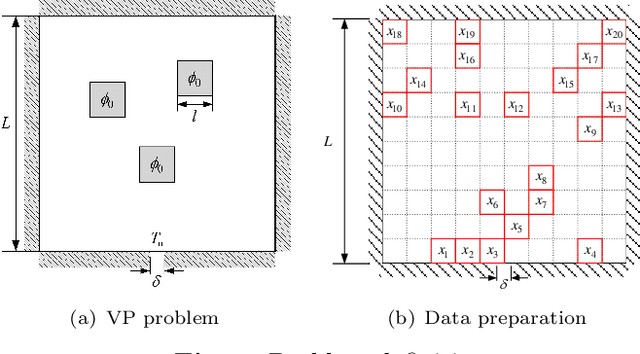
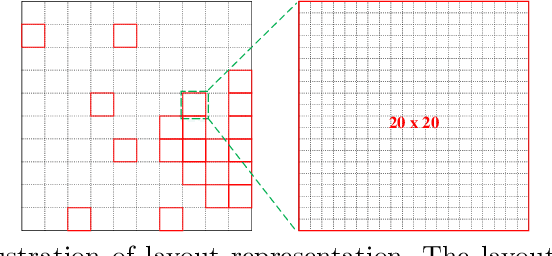
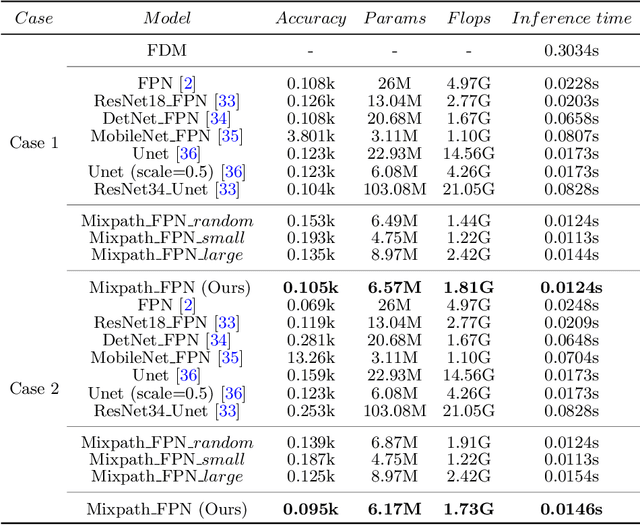
In satellite layout design, heat source layout optimization (HSLO) is an effective technique to decrease the maximum temperature and improve the heat management of the whole system. Recently, deep learning surrogate assisted HSLO has been proposed, which learns the mapping from layout to its corresponding temperature field, so as to substitute the simulation during optimization to decrease the computational cost largely. However, it faces two main challenges: 1) the neural network surrogate for the certain task is often manually designed to be complex and requires rich debugging experience, which is challenging for the designers in the engineering field; 2) existing algorithms for HSLO could only obtain a near optimal solution in single optimization and are easily trapped in local optimum. To address the first challenge, considering reducing the total parameter numbers and ensuring the similar accuracy as well as, a neural architecture search (NAS) method combined with Feature Pyramid Network (FPN) framework is developed to realize the purpose of automatically searching for a small deep learning surrogate model for HSLO. To address the second challenge, a multimodal neighborhood search based layout optimization algorithm (MNSLO) is proposed, which could obtain more and better approximate optimal design schemes simultaneously in single optimization. Finally, two typical two-dimensional heat conduction optimization problems are utilized to demonstrate the effectiveness of the proposed method. With the similar accuracy, NAS finds models with 80% fewer parameters, 64% fewer FLOPs and 36% faster inference time than the original FPN. Besides, with the assistance of deep learning surrogate by automatic search, MNSLO could achieve multiple near optimal design schemes simultaneously to provide more design diversities for designers.

Bayesian Physics-Informed Extreme Learning Machine for Forward and Inverse PDE Problems with Noisy Data

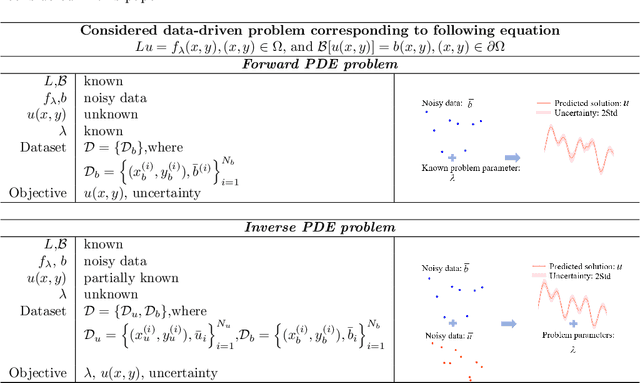
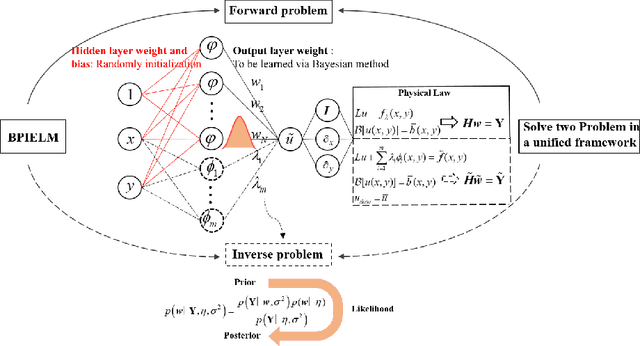
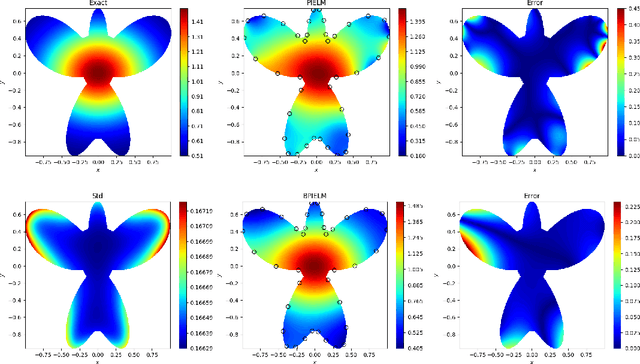
Physics-informed extreme learning machine (PIELM) has recently received significant attention as a rapid version of physics-informed neural network (PINN) for solving partial differential equations (PDEs). The key characteristic is to fix the input layer weights with random values and use Moore-Penrose generalized inverse for the output layer weights. The framework is effective, but it easily suffers from overfitting noisy data and lacks uncertainty quantification for the solution under noise scenarios.To this end, we develop the Bayesian physics-informed extreme learning machine (BPIELM) to solve both forward and inverse linear PDE problems with noisy data in a unified framework. In our framework, a prior probability distribution is introduced in the output layer for extreme learning machine with physic laws and the Bayesian method is used to estimate the posterior of parameters. Besides, for inverse PDE problems, problem parameters considered as new output layer weights are unified in a framework with forward PDE problems. Finally, we demonstrate BPIELM considering both forward problems, including Poisson, advection, and diffusion equations, as well as inverse problems, where unknown problem parameters are estimated. The results show that, compared with PIELM, BPIELM quantifies uncertainty arising from noisy data and provides more accurate predictions. In addition, BPIELM is considerably cheaper than PINN in terms of the computational cost.

RANG: A Residual-based Adaptive Node Generation Method for Physics-Informed Neural Networks

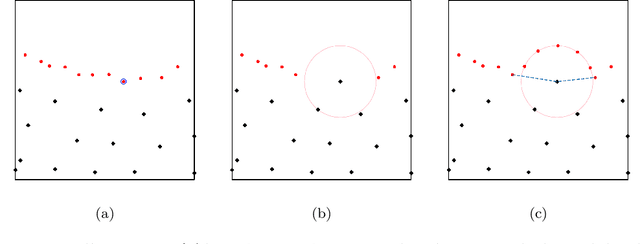
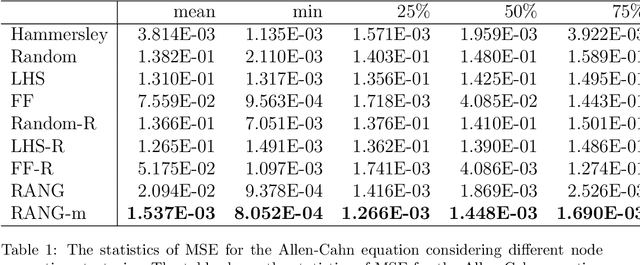
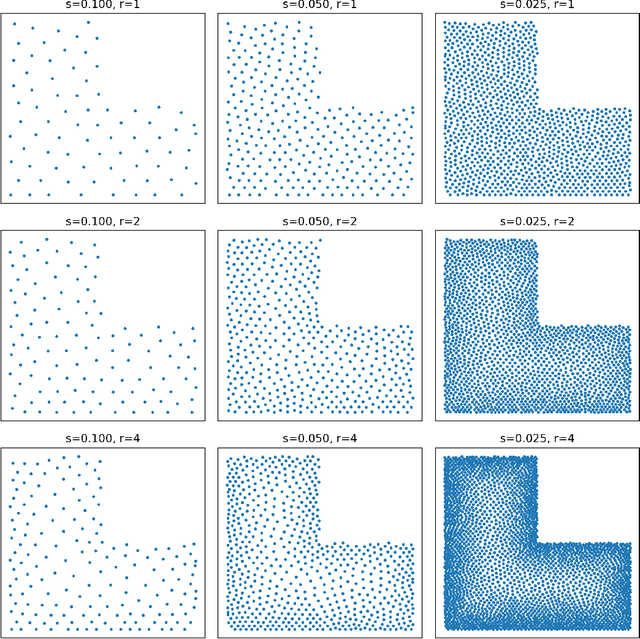
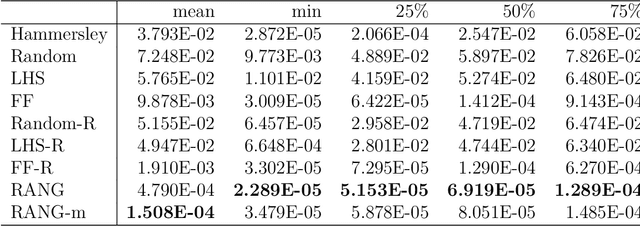
Learning solutions of partial differential equations (PDEs) with Physics-Informed Neural Networks (PINNs) is an attractive alternative approach to traditional solvers due to its flexibility and ease of incorporating observed data. Despite the success of PINNs in accurately solving a wide variety of PDEs, the method still requires improvements in terms of computational efficiency. One possible improvement idea is to optimize the generation of training point sets. Residual-based adaptive sampling and quasi-uniform sampling approaches have been each applied to improve the training effects of PINNs, respectively. To benefit from both methods, we propose the Residual-based Adaptive Node Generation (RANG) approach for efficient training of PINNs, which is based on a variable density nodal distribution method for RBF-FD. The method is also enhanced by a memory mechanism to further improve training stability. We conduct experiments on three linear PDEs and three nonlinear PDEs with various node generation methods, through which the accuracy and efficiency of the proposed method compared to the predominant uniform sampling approach is verified numerically.

Searching for Robust Neural Architectures via Comprehensive and Reliable Evaluation

Neural architecture search (NAS) could help search for robust network architectures, where defining robustness evaluation metrics is the important procedure. However, current robustness evaluations in NAS are not sufficiently comprehensive and reliable. In particular, the common practice only considers adversarial noise and quantified metrics such as the Jacobian matrix, whereas, some studies indicated that the models are also vulnerable to other types of noises such as natural noise. In addition, existing methods taking adversarial noise as the evaluation just use the robust accuracy of the FGSM or PGD, but these adversarial attacks could not provide the adequately reliable evaluation, leading to the vulnerability of the models under stronger attacks. To alleviate the above problems, we propose a novel framework, called Auto Adversarial Attack and Defense (AAAD), where we employ neural architecture search methods, and four types of robustness evaluations are considered, including adversarial noise, natural noise, system noise and quantified metrics, thereby assisting in finding more robust architectures. Also, among the adversarial noise, we use the composite adversarial attack obtained by random search as the new metric to evaluate the robustness of the model architectures. The empirical results on the CIFAR10 dataset show that the searched efficient attack could help find more robust architectures.

Temperature Field Inversion of Heat-Source Systems via Physics-Informed Neural Networks

Temperature field inversion of heat-source systems (TFI-HSS) with limited observations is essential to monitor the system health. Although some methods such as interpolation have been proposed to solve TFI-HSS, those existing methods ignore correlations between data constraints and physics constraints, causing the low precision. In this work, we develop a physics-informed neural network-based temperature field inversion (PINN-TFI) method to solve the TFI-HSS task and a coefficient matrix condition number based position selection of observations (CMCN-PSO) method to select optima positions of noise observations. For the TFI-HSS task, the PINN-TFI method encodes constrain terms into the loss function, thus the task is transformed into an optimization problem of minimizing the loss function. In addition, we have found that noise observations significantly affect reconstruction performances of the PINN-TFI method. To alleviate the effect of noise observations, the CMCN-PSO method is proposed to find optimal positions, where the condition number of observations is used to evaluate positions. The results demonstrate that the PINN-TFI method can significantly improve prediction precisions and the CMCN-PSO method can find good positions to acquire a more robust temperature field.