RecFNO: a resolution-invariant flow and heat field reconstruction method from sparse observations via Fourier neural operator
Paper and Code
Feb 20, 2023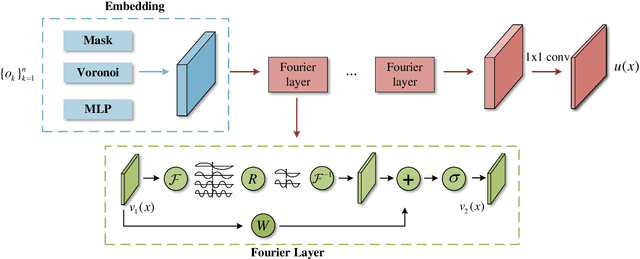
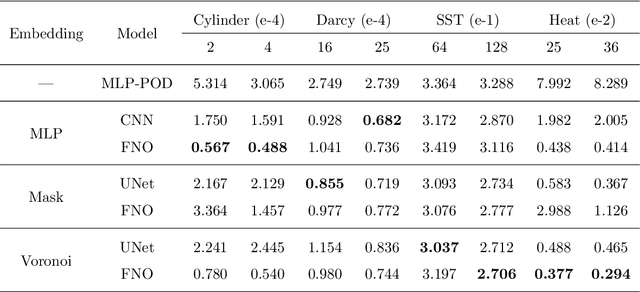

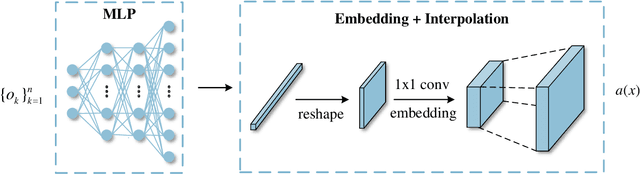
Perception of the full state is an essential technology to support the monitoring, analysis, and design of physical systems, one of whose challenges is to recover global field from sparse observations. Well-known for brilliant approximation ability, deep neural networks have been attractive to data-driven flow and heat field reconstruction studies. However, limited by network structure, existing researches mostly learn the reconstruction mapping in finite-dimensional space and has poor transferability to variable resolution of outputs. In this paper, we extend the new paradigm of neural operator and propose an end-to-end physical field reconstruction method with both excellent performance and mesh transferability named RecFNO. The proposed method aims to learn the mapping from sparse observations to flow and heat field in infinite-dimensional space, contributing to a more powerful nonlinear fitting capacity and resolution-invariant characteristic. Firstly, according to different usage scenarios, we develop three types of embeddings to model the sparse observation inputs: MLP, mask, and Voronoi embedding. The MLP embedding is propitious to more sparse input, while the others benefit from spatial information preservation and perform better with the increase of observation data. Then, we adopt stacked Fourier layers to reconstruct physical field in Fourier space that regularizes the overall recovered field by Fourier modes superposition. Benefiting from the operator in infinite-dimensional space, the proposed method obtains remarkable accuracy and better resolution transferability among meshes. The experiments conducted on fluid mechanics and thermology problems show that the proposed method outperforms existing POD-based and CNN-based methods in most cases and has the capacity to achieve zero-shot super-resolution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge