How to guess a gradient

How much can you say about the gradient of a neural network without computing a loss or knowing the label? This may sound like a strange question: surely the answer is "very little." However, in this paper, we show that gradients are more structured than previously thought. Gradients lie in a predictable low-dimensional subspace which depends on the network architecture and incoming features. Exploiting this structure can significantly improve gradient-free optimization schemes based on directional derivatives, which have struggled to scale beyond small networks trained on toy datasets. We study how to narrow the gap in optimization performance between methods that calculate exact gradients and those that use directional derivatives. Furthermore, we highlight new challenges in overcoming the large gap between optimizing with exact gradients and guessing the gradients.

Learning to Transform for Generalizable Instance-wise Invariance

Computer vision research has long aimed to build systems that are robust to spatial transformations found in natural data. Traditionally, this is done using data augmentation or hard-coding invariances into the architecture. However, too much or too little invariance can hurt, and the correct amount is unknown a priori and dependent on the instance. Ideally, the appropriate invariance would be learned from data and inferred at test-time. We treat invariance as a prediction problem. Given any image, we use a normalizing flow to predict a distribution over transformations and average the predictions over them. Since this distribution only depends on the instance, we can align instances before classifying them and generalize invariance across classes. The same distribution can also be used to adapt to out-of-distribution poses. This normalizing flow is trained end-to-end and can learn a much larger range of transformations than Augerino and InstaAug. When used as data augmentation, our method shows accuracy and robustness gains on CIFAR 10, CIFAR10-LT, and TinyImageNet.

Multi-Spectral Image Classification with Ultra-Lean Complex-Valued Models

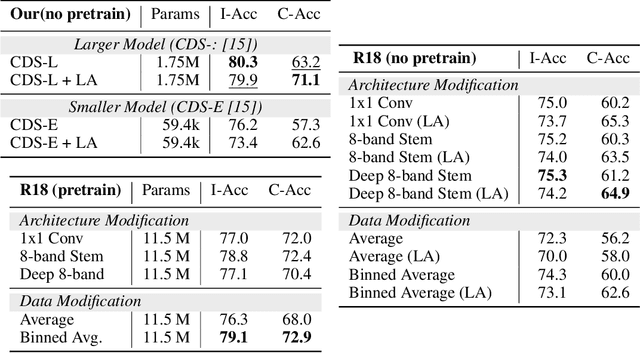
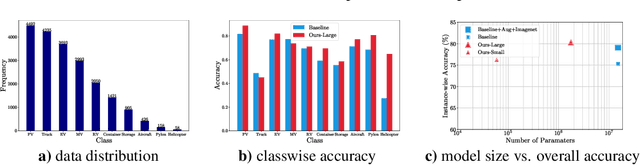
Multi-spectral imagery is invaluable for remote sensing due to different spectral signatures exhibited by materials that often appear identical in greyscale and RGB imagery. Paired with modern deep learning methods, this modality has great potential utility in a variety of remote sensing applications, such as humanitarian assistance and disaster recovery efforts. State-of-the-art deep learning methods have greatly benefited from large-scale annotations like in ImageNet, but existing MSI image datasets lack annotations at a similar scale. As an alternative to transfer learning on such data with few annotations, we apply complex-valued co-domain symmetric models to classify real-valued MSI images. Our experiments on 8-band xView data show that our ultra-lean model trained on xView from scratch without data augmentations can outperform ResNet with data augmentation and modified transfer learning on xView. Our work is the first to demonstrate the value of complex-valued deep learning on real-valued MSI data.

Co-domain Symmetry for Complex-Valued Deep Learning

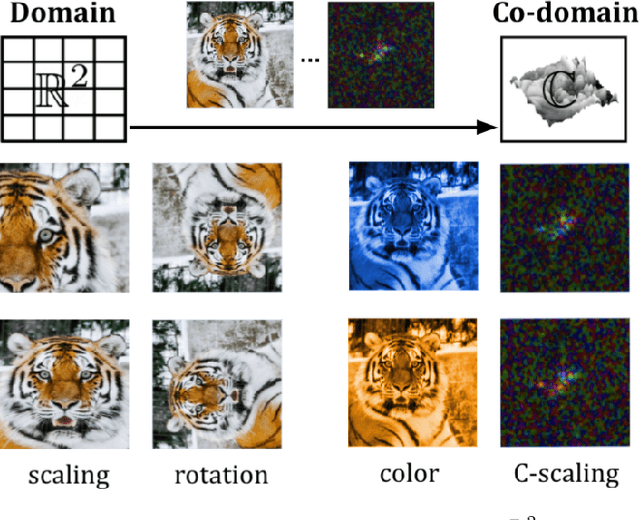
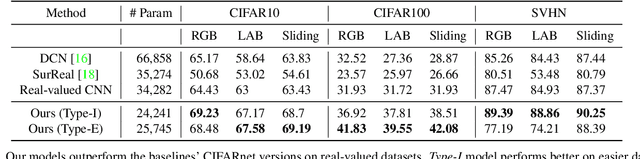
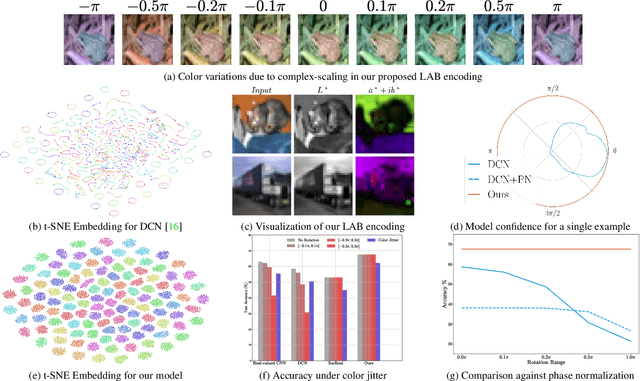
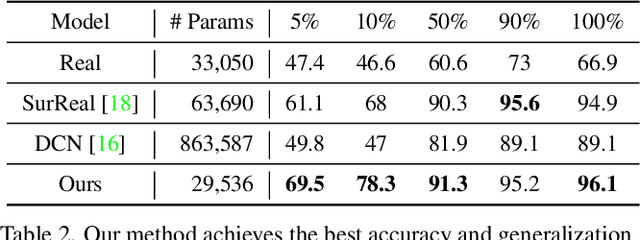
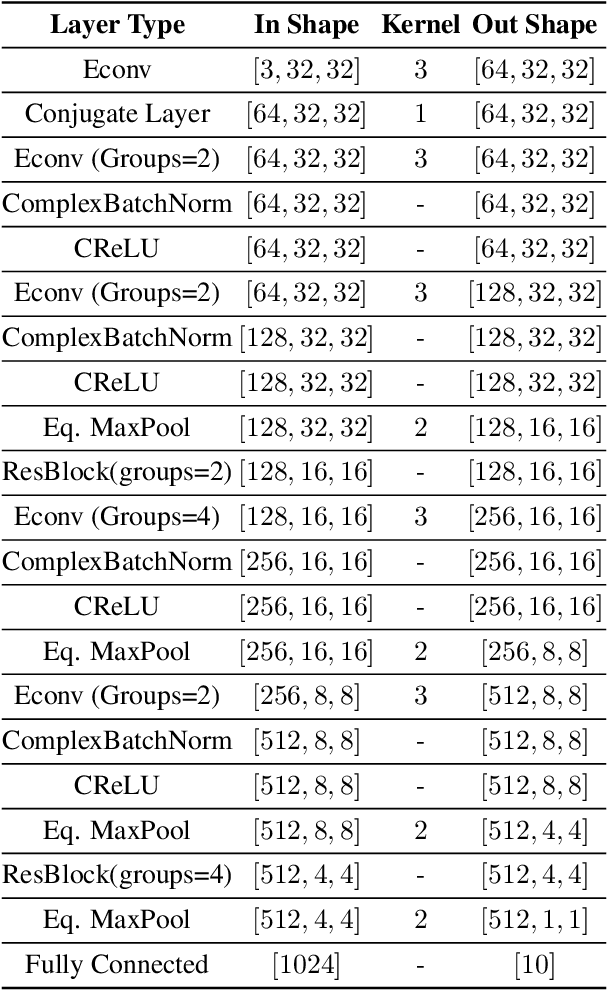
We study complex-valued scaling as a type of symmetry natural and unique to complex-valued measurements and representations. Deep Complex Networks (DCN) extends real-valued algebra to the complex domain without addressing complex-valued scaling. SurReal takes a restrictive manifold view of complex numbers, adopting a distance metric to achieve complex-scaling invariance while losing rich complex-valued information. We analyze complex-valued scaling as a co-domain transformation and design novel equivariant and invariant neural network layer functions for this special transformation. We also propose novel complex-valued representations of RGB images, where complex-valued scaling indicates hue shift or correlated changes across color channels. Benchmarked on MSTAR, CIFAR10, CIFAR100, and SVHN, our co-domain symmetric (CDS) classifiers deliver higher accuracy, better generalization, robustness to co-domain transformations, and lower model bias and variance than DCN and SurReal with far fewer parameters.

Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains

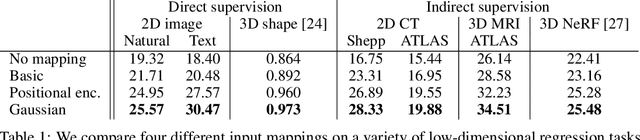
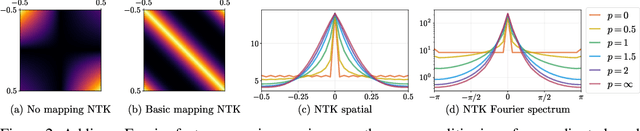
We show that passing input points through a simple Fourier feature mapping enables a multilayer perceptron (MLP) to learn high-frequency functions in low-dimensional problem domains. These results shed light on recent advances in computer vision and graphics that achieve state-of-the-art results by using MLPs to represent complex 3D objects and scenes. Using tools from the neural tangent kernel (NTK) literature, we show that a standard MLP fails to learn high frequencies both in theory and in practice. To overcome this spectral bias, we use a Fourier feature mapping to transform the effective NTK into a stationary kernel with a tunable bandwidth. We suggest an approach for selecting problem-specific Fourier features that greatly improves the performance of MLPs for low-dimensional regression tasks relevant to the computer vision and graphics communities.