Co-domain Symmetry for Complex-Valued Deep Learning
Paper and Code
Dec 02, 2021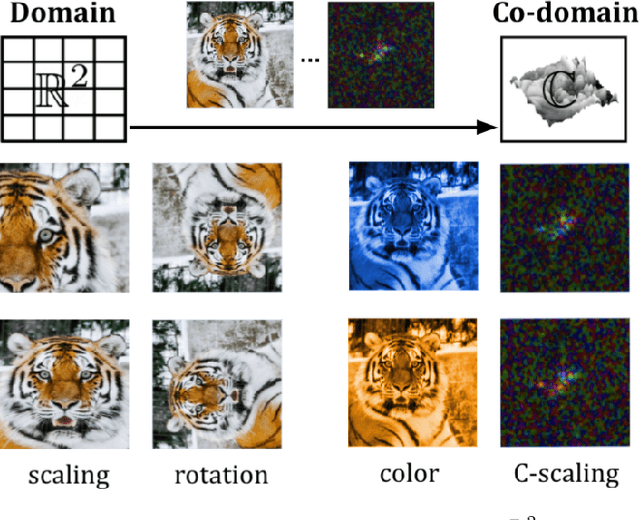
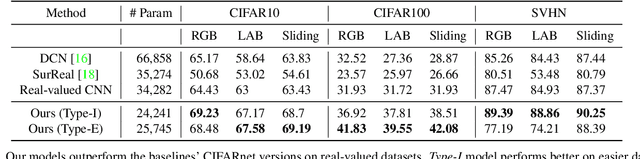
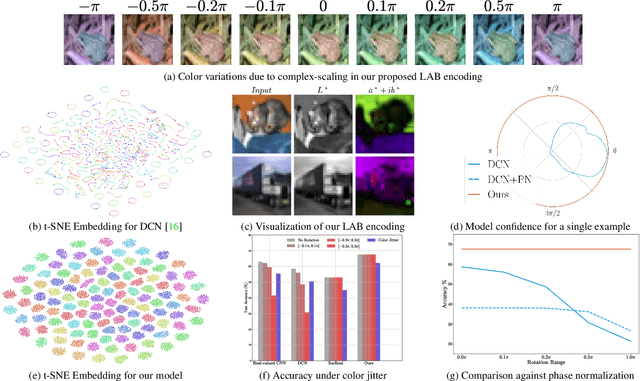
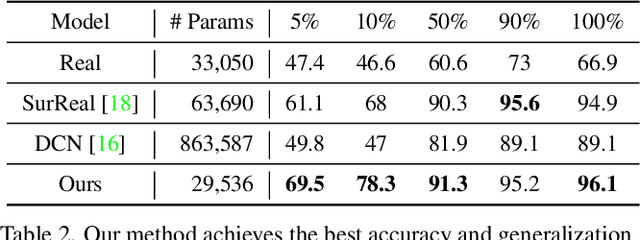
We study complex-valued scaling as a type of symmetry natural and unique to complex-valued measurements and representations. Deep Complex Networks (DCN) extends real-valued algebra to the complex domain without addressing complex-valued scaling. SurReal takes a restrictive manifold view of complex numbers, adopting a distance metric to achieve complex-scaling invariance while losing rich complex-valued information. We analyze complex-valued scaling as a co-domain transformation and design novel equivariant and invariant neural network layer functions for this special transformation. We also propose novel complex-valued representations of RGB images, where complex-valued scaling indicates hue shift or correlated changes across color channels. Benchmarked on MSTAR, CIFAR10, CIFAR100, and SVHN, our co-domain symmetric (CDS) classifiers deliver higher accuracy, better generalization, robustness to co-domain transformations, and lower model bias and variance than DCN and SurReal with far fewer parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge