AlignMamba: Enhancing Multimodal Mamba with Local and Global Cross-modal Alignment

Cross-modal alignment is crucial for multimodal representation fusion due to the inherent heterogeneity between modalities. While Transformer-based methods have shown promising results in modeling inter-modal relationships, their quadratic computational complexity limits their applicability to long-sequence or large-scale data. Although recent Mamba-based approaches achieve linear complexity, their sequential scanning mechanism poses fundamental challenges in comprehensively modeling cross-modal relationships. To address this limitation, we propose AlignMamba, an efficient and effective method for multimodal fusion. Specifically, grounded in Optimal Transport, we introduce a local cross-modal alignment module that explicitly learns token-level correspondences between different modalities. Moreover, we propose a global cross-modal alignment loss based on Maximum Mean Discrepancy to implicitly enforce the consistency between different modal distributions. Finally, the unimodal representations after local and global alignment are passed to the Mamba backbone for further cross-modal interaction and multimodal fusion. Extensive experiments on complete and incomplete multimodal fusion tasks demonstrate the effectiveness and efficiency of the proposed method.

EMMA: Empowering Multi-modal Mamba with Structural and Hierarchical Alignment

Mamba-based architectures have shown to be a promising new direction for deep learning models owing to their competitive performance and sub-quadratic deployment speed. However, current Mamba multi-modal large language models (MLLM) are insufficient in extracting visual features, leading to imbalanced cross-modal alignment between visual and textural latents, negatively impacting performance on multi-modal tasks. In this work, we propose Empowering Multi-modal Mamba with Structural and Hierarchical Alignment (EMMA), which enables the MLLM to extract fine-grained visual information. Specifically, we propose a pixel-wise alignment module to autoregressively optimize the learning and processing of spatial image-level features along with textual tokens, enabling structural alignment at the image level. In addition, to prevent the degradation of visual information during the cross-model alignment process, we propose a multi-scale feature fusion (MFF) module to combine multi-scale visual features from intermediate layers, enabling hierarchical alignment at the feature level. Extensive experiments are conducted across a variety of multi-modal benchmarks. Our model shows lower latency than other Mamba-based MLLMs and is nearly four times faster than transformer-based MLLMs of similar scale during inference. Due to better cross-modal alignment, our model exhibits lower degrees of hallucination and enhanced sensitivity to visual details, which manifests in superior performance across diverse multi-modal benchmarks. Code will be provided.

Co-domain Symmetry for Complex-Valued Deep Learning

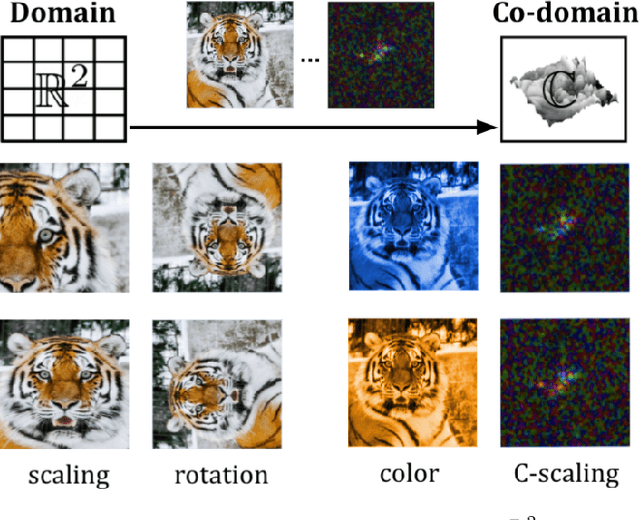
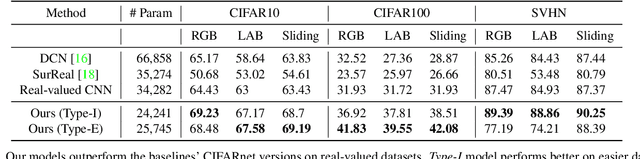
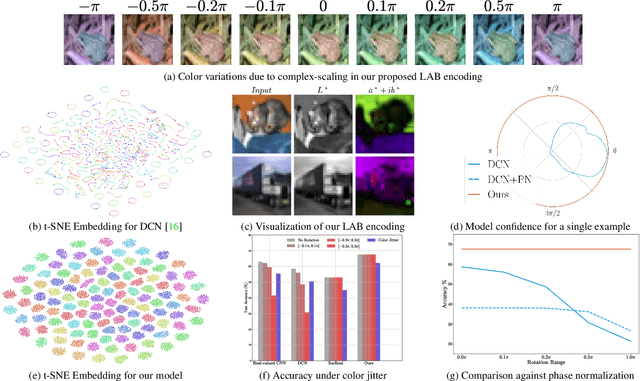
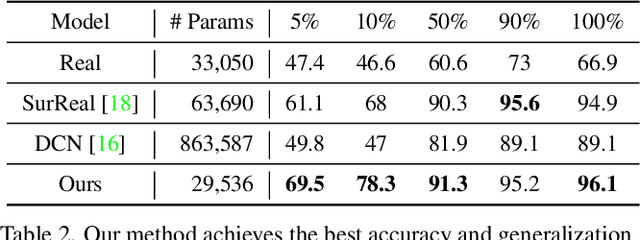
We study complex-valued scaling as a type of symmetry natural and unique to complex-valued measurements and representations. Deep Complex Networks (DCN) extends real-valued algebra to the complex domain without addressing complex-valued scaling. SurReal takes a restrictive manifold view of complex numbers, adopting a distance metric to achieve complex-scaling invariance while losing rich complex-valued information. We analyze complex-valued scaling as a co-domain transformation and design novel equivariant and invariant neural network layer functions for this special transformation. We also propose novel complex-valued representations of RGB images, where complex-valued scaling indicates hue shift or correlated changes across color channels. Benchmarked on MSTAR, CIFAR10, CIFAR100, and SVHN, our co-domain symmetric (CDS) classifiers deliver higher accuracy, better generalization, robustness to co-domain transformations, and lower model bias and variance than DCN and SurReal with far fewer parameters.

C-SURE: Shrinkage Estimator and Prototype Classifier for Complex-Valued Deep Learning

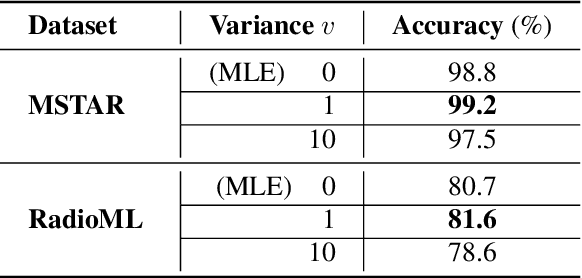
The James-Stein (JS) shrinkage estimator is a biased estimator that captures the mean of Gaussian random vectors.While it has a desirable statistical property of dominance over the maximum likelihood estimator (MLE) in terms of mean squared error (MSE), not much progress has been made on extending the estimator onto manifold-valued data. We propose C-SURE, a novel Stein's unbiased risk estimate (SURE) of the JS estimator on the manifold of complex-valued data with a theoretically proven optimum over MLE. Adapting the architecture of the complex-valued SurReal classifier, we further incorporate C-SURE into a prototype convolutional neural network (CNN) classifier. We compare C-SURE with SurReal and a real-valued baseline on complex-valued MSTAR and RadioML datasets. C-SURE is more accurate and robust than SurReal, and the shrinkage estimator is always better than MLE for the same prototype classifier. Like SurReal, C-SURE is much smaller, outperforming the real-valued baseline on MSTAR (RadioML) with less than 1 percent (3 percent) of the baseline size

Surreal: Complex-Valued Deep Learning as Principled Transformations on a Rotational Lie Group

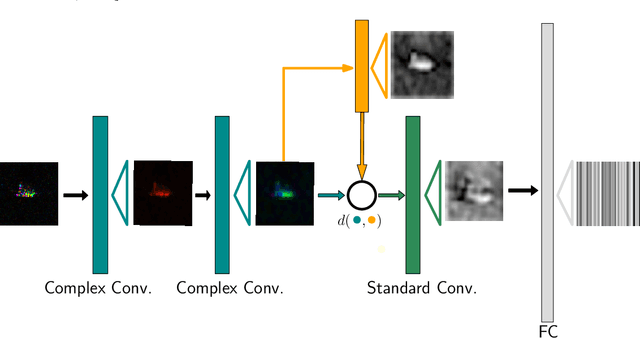
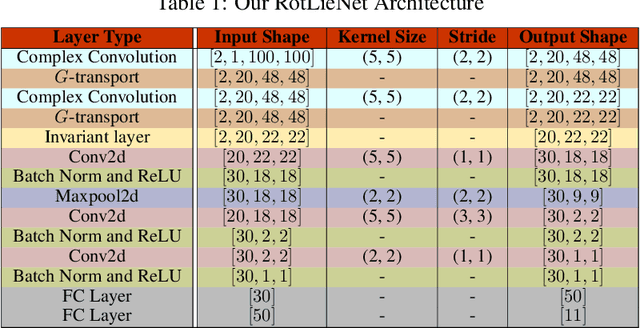
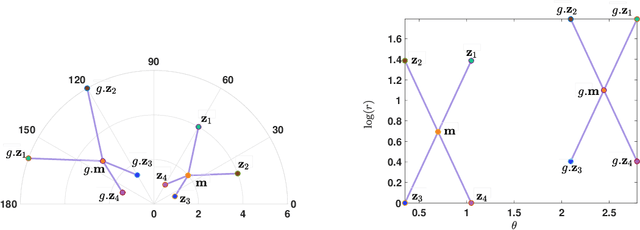
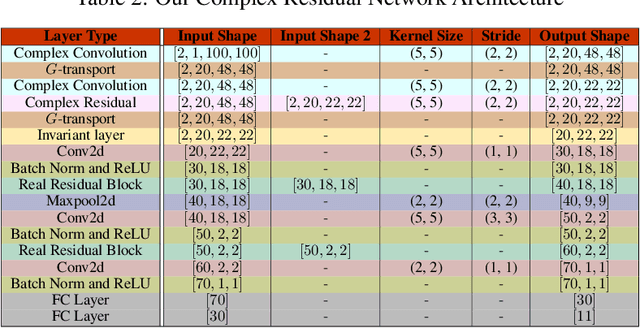
Complex-valued deep learning has attracted increasing attention in recent years, due to its versatility and ability to capture more information. However, the lack of well-defined complex-valued operations remains a bottleneck for further advancement. In this work, we propose a geometric way to define deep neural networks on the space of complex numbers by utilizing weighted Fr\'echet mean. We mathematically prove the viability of our algorithm. We also define basic building blocks such as convolution, non-linearity, and residual connections tailored for the space of complex numbers. To demonstrate the effectiveness of our proposed model, we compare our complex-valued network comprehensively with its real state-of-the-art counterpart on the MSTAR classification task and achieve better performance, while utilizing less than 1% of the parameters.