Surreal: Complex-Valued Deep Learning as Principled Transformations on a Rotational Lie Group
Paper and Code
Oct 18, 2019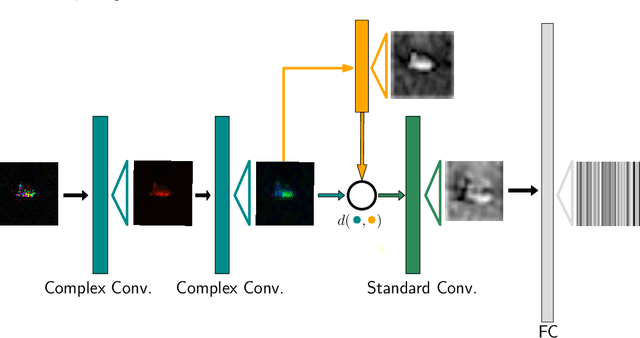
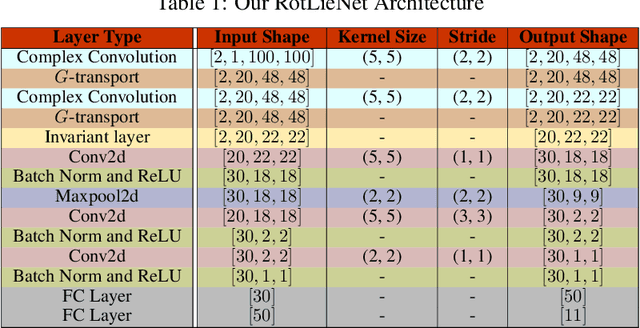
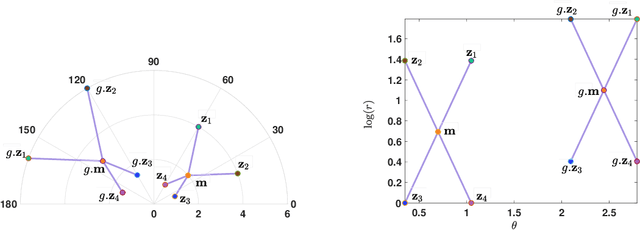
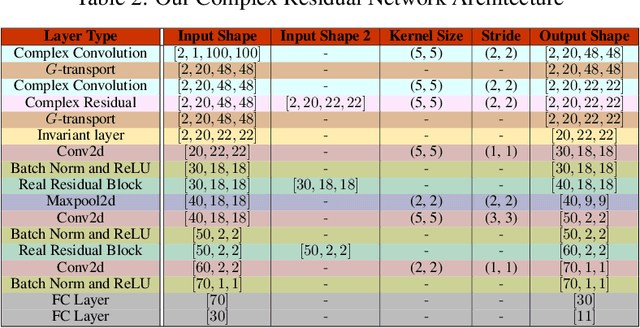
Complex-valued deep learning has attracted increasing attention in recent years, due to its versatility and ability to capture more information. However, the lack of well-defined complex-valued operations remains a bottleneck for further advancement. In this work, we propose a geometric way to define deep neural networks on the space of complex numbers by utilizing weighted Fr\'echet mean. We mathematically prove the viability of our algorithm. We also define basic building blocks such as convolution, non-linearity, and residual connections tailored for the space of complex numbers. To demonstrate the effectiveness of our proposed model, we compare our complex-valued network comprehensively with its real state-of-the-art counterpart on the MSTAR classification task and achieve better performance, while utilizing less than 1% of the parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge