Scaling Integer Arithmetic in Probabilistic Programs

Distributions on integers are ubiquitous in probabilistic modeling but remain challenging for many of today's probabilistic programming languages (PPLs). The core challenge comes from discrete structure: many of today's PPL inference strategies rely on enumeration, sampling, or differentiation in order to scale, which fail for high-dimensional complex discrete distributions involving integers. Our insight is that there is structure in arithmetic that these approaches are not using. We present a binary encoding strategy for discrete distributions that exploits the rich logical structure of integer operations like summation and comparison. We leverage this structured encoding with knowledge compilation to perform exact probabilistic inference, and show that this approach scales to much larger integer distributions with arithmetic.

flip-hoisting: Exploiting Repeated Parameters in Discrete Probabilistic Programs

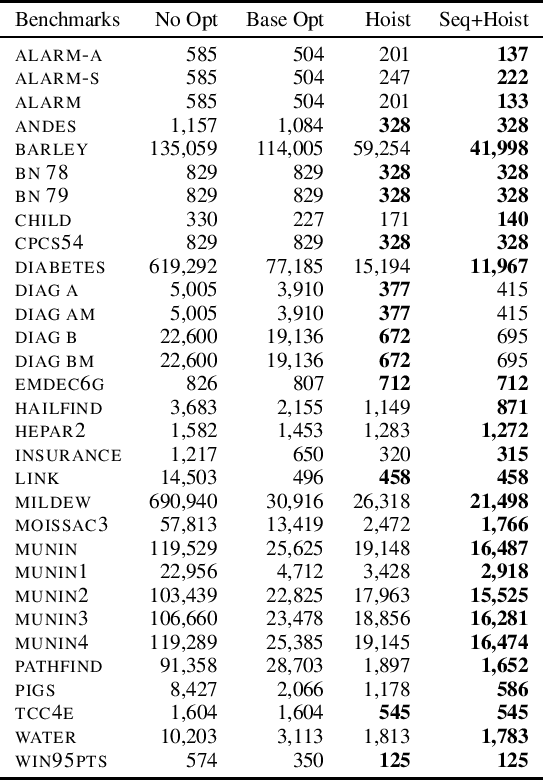
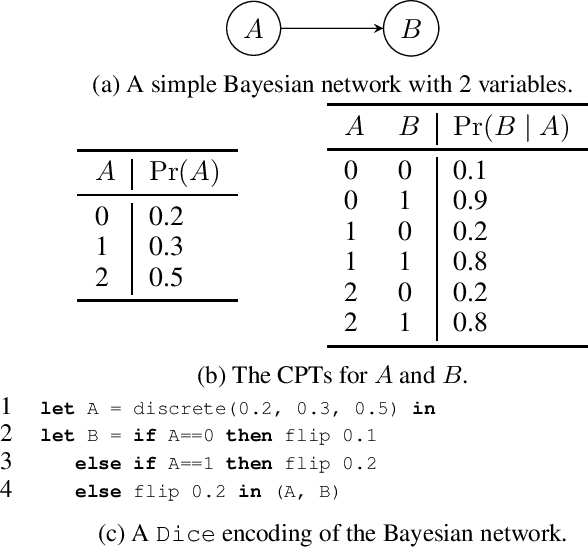
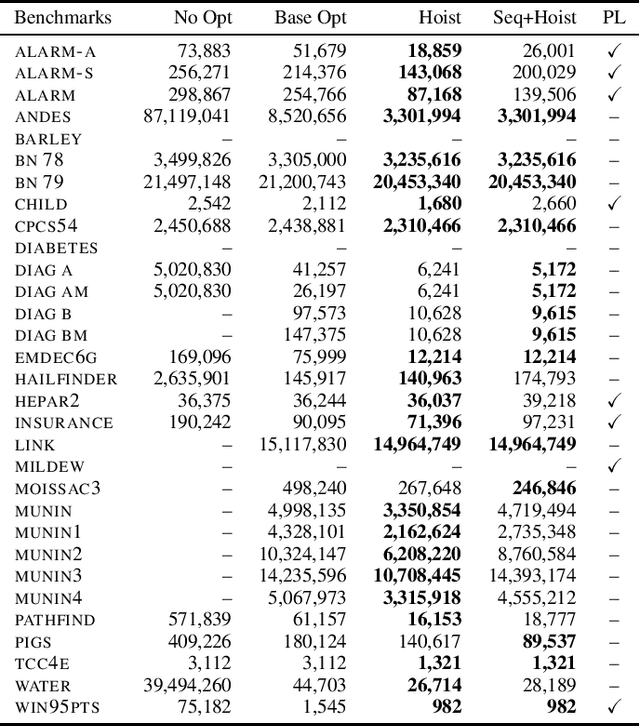
Probabilistic programming is emerging as a popular and effective means of probabilistic modeling and an alternative to probabilistic graphical models. Probabilistic programs provide greater expressivity and flexibility in modeling probabilistic systems than graphical models, but this flexibility comes at a cost: there remains a significant disparity in performance between specialized Bayesian network solvers and probabilistic program inference algorithms. In this work we present a program analysis and associated optimization, flip-hoisting, that collapses repetitious parameters in discrete probabilistic programs to improve inference performance. flip-hoisting generalizes parameter sharing - a well-known important optimization from discrete graphical models - to probabilistic programs. We implement flip-hoisting in an existing probabilistic programming language and show empirically that it significantly improves inference performance, narrowing the gap between the performances of probabilistic programs and probabilistic graphical models.

Counterexample-Guided Learning of Monotonic Neural Networks

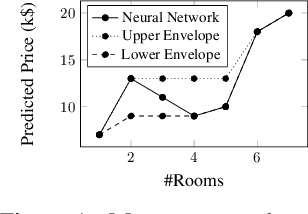
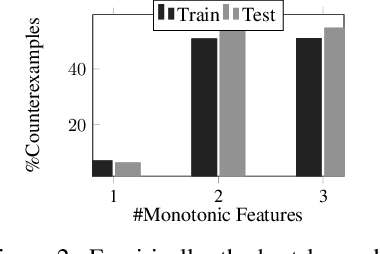
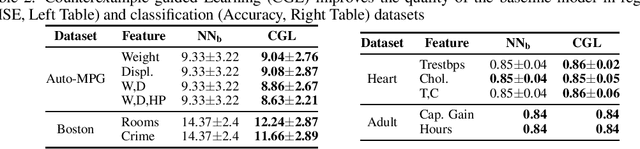
The widespread adoption of deep learning is often attributed to its automatic feature construction with minimal inductive bias. However, in many real-world tasks, the learned function is intended to satisfy domain-specific constraints. We focus on monotonicity constraints, which are common and require that the function's output increases with increasing values of specific input features. We develop a counterexample-guided technique to provably enforce monotonicity constraints at prediction time. Additionally, we propose a technique to use monotonicity as an inductive bias for deep learning. It works by iteratively incorporating monotonicity counterexamples in the learning process. Contrary to prior work in monotonic learning, we target general ReLU neural networks and do not further restrict the hypothesis space. We have implemented these techniques in a tool called COMET. Experiments on real-world datasets demonstrate that our approach achieves state-of-the-art results compared to existing monotonic learners, and can improve the model quality compared to those that were trained without taking monotonicity constraints into account.

Overfitting in Synthesis: Theory and Practice (Extender Version)

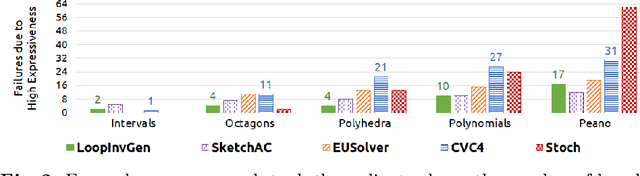
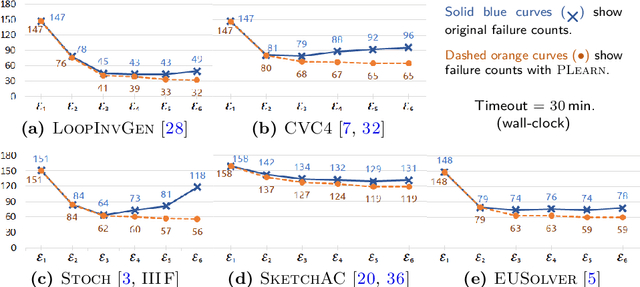
In syntax-guided synthesis (SyGuS), a synthesizer's goal is to automatically generate a program belonging to a grammar of possible implementations that meets a logical specification. We investigate a common limitation across state-of-the-art SyGuS tools that perform counterexample-guided inductive synthesis (CEGIS). We empirically observe that as the expressiveness of the provided grammar increases, the performance of these tools degrades significantly. We claim that this degradation is not only due to a larger search space, but also due to overfitting. We formally define this phenomenon and prove no-free-lunch theorems for SyGuS, which reveal a fundamental tradeoff between synthesizer performance and grammar expressiveness. A standard approach to mitigate overfitting in machine learning is to run multiple learners with varying expressiveness in parallel. We demonstrate that this insight can immediately benefit existing SyGuS tools. We also propose a novel single-threaded technique called hybrid enumeration that interleaves different grammars and outperforms the winner of the 2018 SyGuS competition (Inv track), solving more problems and achieving a $5\times$ mean speedup.

Generating and Sampling Orbits for Lifted Probabilistic Inference

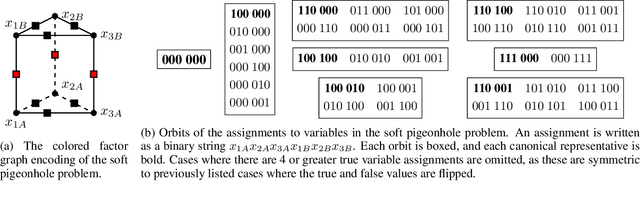
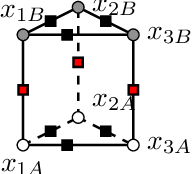
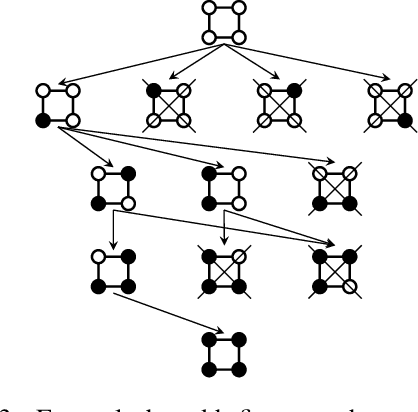
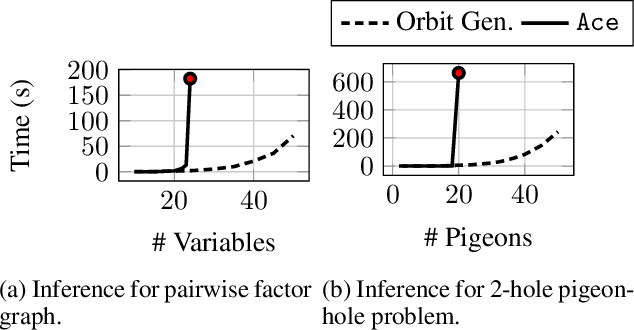
Lifted inference scales to large probability models by exploiting symmetry. However, existing exact lifted inference techniques do not apply to general factor graphs, as they require a relational representation. In this work we provide a theoretical framework and algorithm for performing exact lifted inference on symmetric factor graphs by computing colored graph automorphisms, as is often done for approximate lifted inference. Our key insight is to represent variable assignments directly in the colored factor graph encoding. This allows us to generate representatives and compute the size of each orbit of the symmetric distribution. In addition to exact inference, we use this encoding to implement an MCMC algorithm that explores the space of orbits quickly by uniform orbit sampling.

LoopInvGen: A Loop Invariant Generator based on Precondition Inference

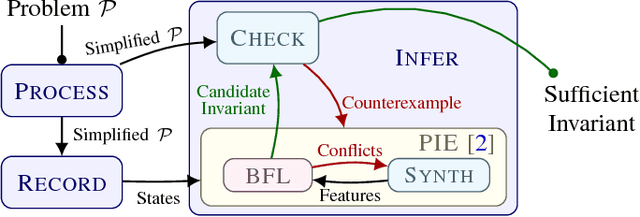
We describe the LoopInvGen tool for generating loop invariants that can provably guarantee correctness of a program with respect to a given specification. LoopInvGen is an efficient implementation of the inference technique originally proposed in our earlier work on PIE (https://doi.org/10.1145/2908080.2908099). In contrast to existing techniques, LoopInvGen is not restricted to a fixed set of features -- atomic predicates that are composed together to build complex loop invariants. Instead, we start with no initial features, and use program synthesis techniques to grow the set on demand. This not only enables a less onerous and more expressive approach, but also appears to be significantly faster than the existing tools over the SyGuS-COMP 2017 benchmarks from the INV track.

FlashProfile: Interactive Synthesis of Syntactic Profiles

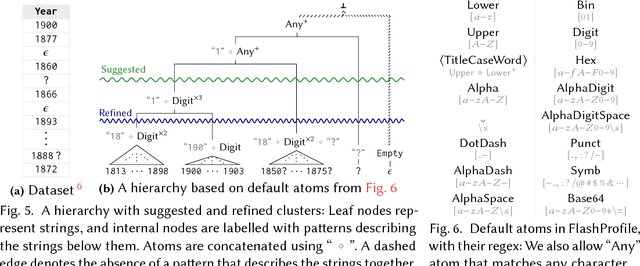
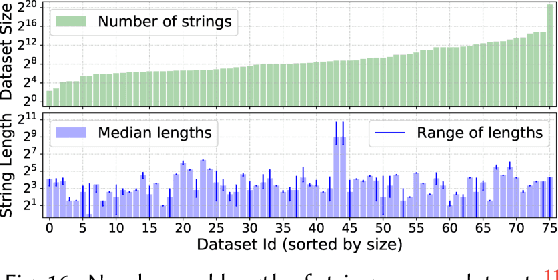
We address the problem of learning comprehensive syntactic profiles for a set of strings. Real-world datasets, typically curated from multiple sources, often contain data in various formats. Thus any data processing task is preceded by the critical step of data format identification. However, manual inspection of data to identify various formats is infeasible in standard big-data scenarios. We present a technique for generating comprehensive syntactic profiles in terms of user-defined patterns that also allows for interactive refinement. We define a syntactic profile as a set of succinct patterns that describe the entire dataset. Our approach efficiently learns such profiles, and allows refinement by exposing a desired number of patterns. Our implementation, FlashProfile, shows a median profiling time of 0.7s over 142 tasks on 74 real datasets. We also show that access to the generated data profiles allow for more accurate synthesis of programs, using fewer examples in programming-by-example workflows.

Probabilistic Program Abstractions

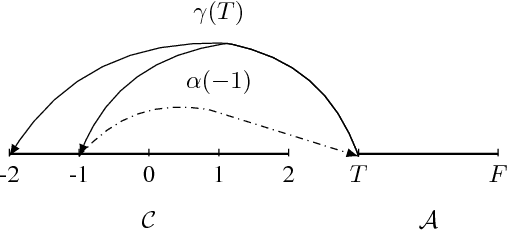
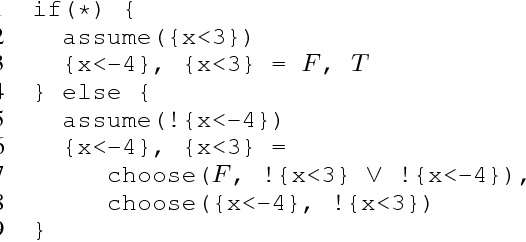
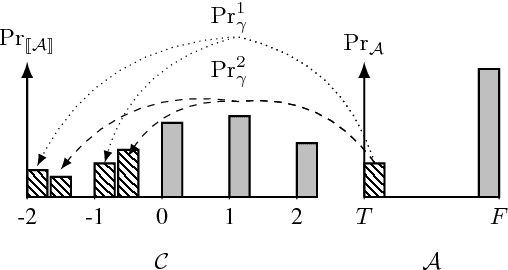
Abstraction is a fundamental tool for reasoning about complex systems. Program abstraction has been utilized to great effect for analyzing deterministic programs. At the heart of program abstraction is the relationship between a concrete program, which is difficult to analyze, and an abstract program, which is more tractable. Program abstractions, however, are typically not probabilistic. We generalize non-deterministic program abstractions to probabilistic program abstractions by explicitly quantifying the non-deterministic choices. Our framework upgrades key definitions and properties of abstractions to the probabilistic context. We also discuss preliminary ideas for performing inference on probabilistic abstractions and general probabilistic programs.