Scaling Integer Arithmetic in Probabilistic Programs

Distributions on integers are ubiquitous in probabilistic modeling but remain challenging for many of today's probabilistic programming languages (PPLs). The core challenge comes from discrete structure: many of today's PPL inference strategies rely on enumeration, sampling, or differentiation in order to scale, which fail for high-dimensional complex discrete distributions involving integers. Our insight is that there is structure in arithmetic that these approaches are not using. We present a binary encoding strategy for discrete distributions that exploits the rich logical structure of integer operations like summation and comparison. We leverage this structured encoding with knowledge compilation to perform exact probabilistic inference, and show that this approach scales to much larger integer distributions with arithmetic.

Type Prediction With Program Decomposition and Fill-in-the-Type Training

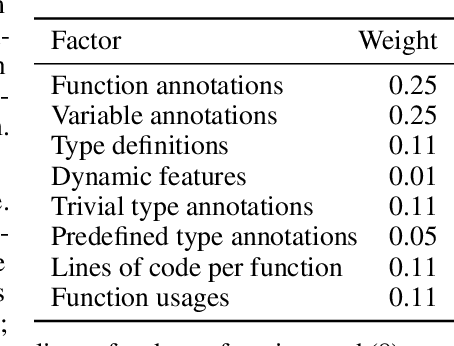
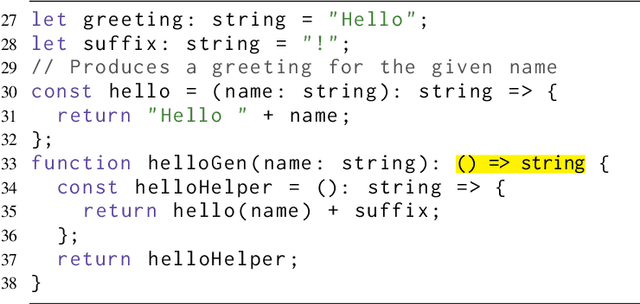
TypeScript and Python are two programming languages that support optional type annotations, which are useful but tedious to introduce and maintain. This has motivated automated type prediction: given an untyped program, produce a well-typed output program. Large language models (LLMs) are promising for type prediction, but there are challenges: fill-in-the-middle performs poorly, programs may not fit into the context window, generated types may not type check, and it is difficult to measure how well-typed the output program is. We address these challenges by building OpenTau, a search-based approach for type prediction that leverages large language models. We propose a new metric for type prediction quality, give a tree-based program decomposition that searches a space of generated types, and present fill-in-the-type fine-tuning for LLMs. We evaluate our work with a new dataset for TypeScript type prediction, and show that 47.4% of files type check (14.5% absolute improvement) with an overall rate of 3.3 type errors per file. All code, data, and models are available at: https://github.com/GammaTauAI/opentau.

flip-hoisting: Exploiting Repeated Parameters in Discrete Probabilistic Programs

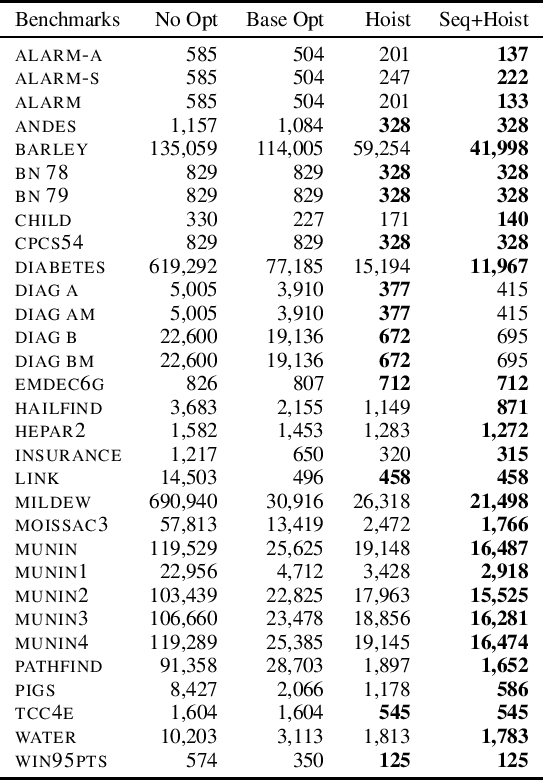
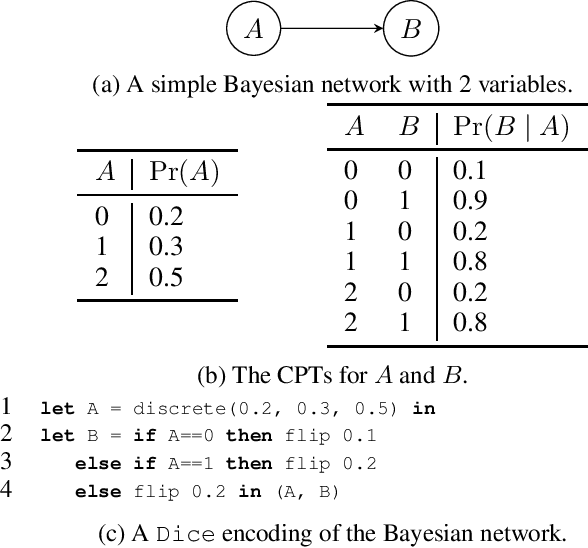
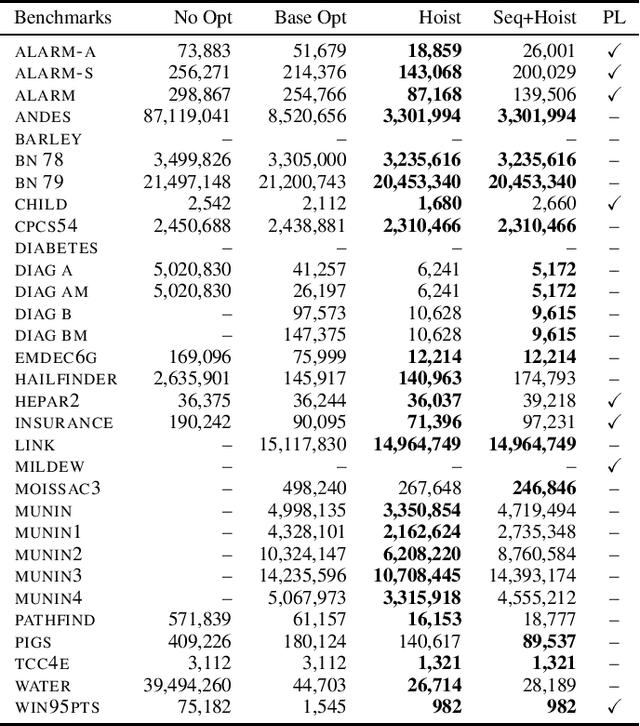
Probabilistic programming is emerging as a popular and effective means of probabilistic modeling and an alternative to probabilistic graphical models. Probabilistic programs provide greater expressivity and flexibility in modeling probabilistic systems than graphical models, but this flexibility comes at a cost: there remains a significant disparity in performance between specialized Bayesian network solvers and probabilistic program inference algorithms. In this work we present a program analysis and associated optimization, flip-hoisting, that collapses repetitious parameters in discrete probabilistic programs to improve inference performance. flip-hoisting generalizes parameter sharing - a well-known important optimization from discrete graphical models - to probabilistic programs. We implement flip-hoisting in an existing probabilistic programming language and show empirically that it significantly improves inference performance, narrowing the gap between the performances of probabilistic programs and probabilistic graphical models.

On the Relationship Between Probabilistic Circuits and Determinantal Point Processes

Scaling probabilistic models to large realistic problems and datasets is a key challenge in machine learning. Central to this effort is the development of tractable probabilistic models (TPMs): models whose structure guarantees efficient probabilistic inference algorithms. The current landscape of TPMs is fragmented: there exist various kinds of TPMs with different strengths and weaknesses. Two of the most prominent classes of TPMs are determinantal point processes (DPPs) and probabilistic circuits (PCs). This paper provides the first systematic study of their relationship. We propose a unified analysis and shared language for discussing DPPs and PCs. Then we establish theoretical barriers for the unification of these two families, and prove that there are cases where DPPs have no compact representation as a class of PCs. We close with a perspective on the central problem of unifying these tractable models.

Generating and Sampling Orbits for Lifted Probabilistic Inference

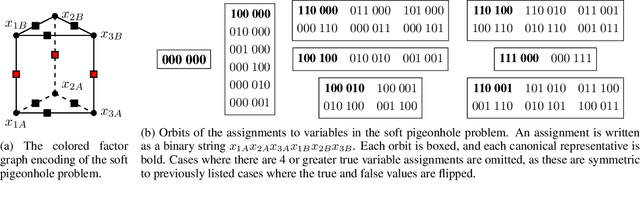
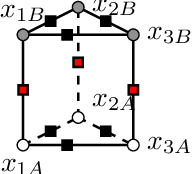
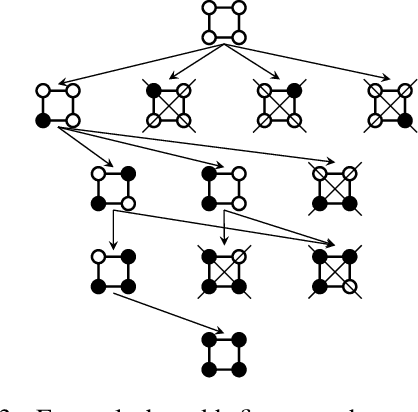
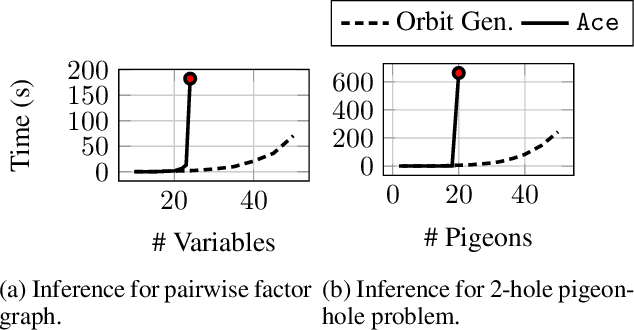
Lifted inference scales to large probability models by exploiting symmetry. However, existing exact lifted inference techniques do not apply to general factor graphs, as they require a relational representation. In this work we provide a theoretical framework and algorithm for performing exact lifted inference on symmetric factor graphs by computing colored graph automorphisms, as is often done for approximate lifted inference. Our key insight is to represent variable assignments directly in the colored factor graph encoding. This allows us to generate representatives and compute the size of each orbit of the symmetric distribution. In addition to exact inference, we use this encoding to implement an MCMC algorithm that explores the space of orbits quickly by uniform orbit sampling.

Probabilistic Program Abstractions

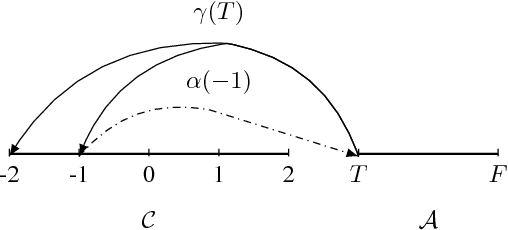
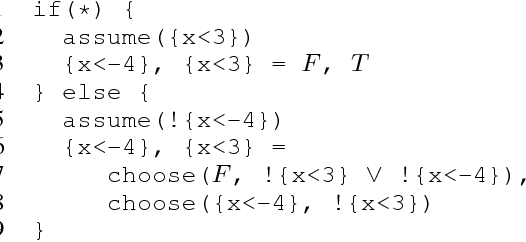
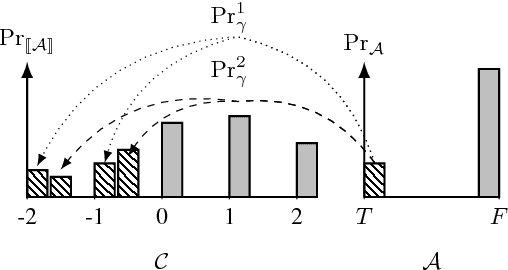
Abstraction is a fundamental tool for reasoning about complex systems. Program abstraction has been utilized to great effect for analyzing deterministic programs. At the heart of program abstraction is the relationship between a concrete program, which is difficult to analyze, and an abstract program, which is more tractable. Program abstractions, however, are typically not probabilistic. We generalize non-deterministic program abstractions to probabilistic program abstractions by explicitly quantifying the non-deterministic choices. Our framework upgrades key definitions and properties of abstractions to the probabilistic context. We also discuss preliminary ideas for performing inference on probabilistic abstractions and general probabilistic programs.