Generating and Sampling Orbits for Lifted Probabilistic Inference

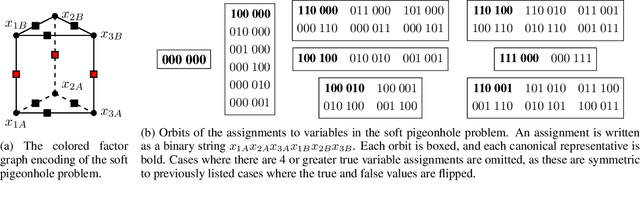
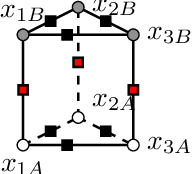
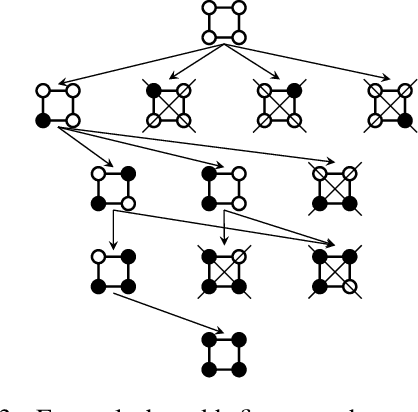
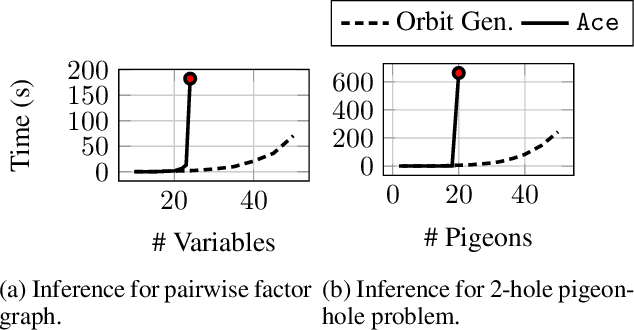
Lifted inference scales to large probability models by exploiting symmetry. However, existing exact lifted inference techniques do not apply to general factor graphs, as they require a relational representation. In this work we provide a theoretical framework and algorithm for performing exact lifted inference on symmetric factor graphs by computing colored graph automorphisms, as is often done for approximate lifted inference. Our key insight is to represent variable assignments directly in the colored factor graph encoding. This allows us to generate representatives and compute the size of each orbit of the symmetric distribution. In addition to exact inference, we use this encoding to implement an MCMC algorithm that explores the space of orbits quickly by uniform orbit sampling.