Thibaut Lienart
Amazon SageMaker Autopilot: a white box AutoML solution at scale
Dec 16, 2020
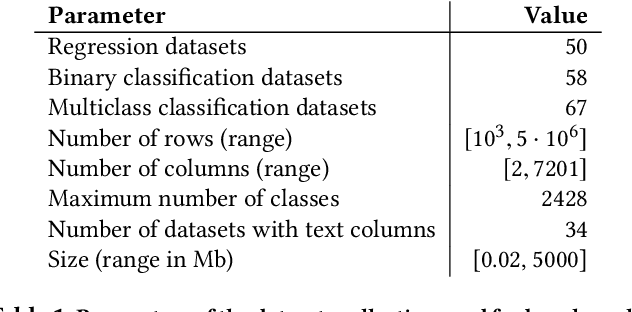
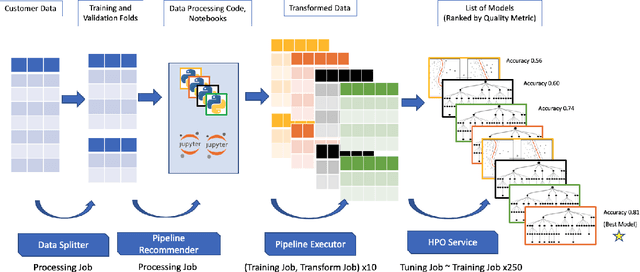
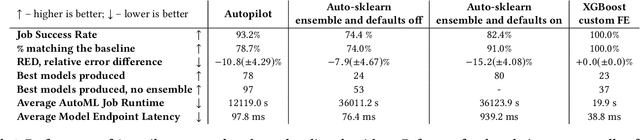
Abstract:AutoML systems provide a black-box solution to machine learning problems by selecting the right way of processing features, choosing an algorithm and tuning the hyperparameters of the entire pipeline. Although these systems perform well on many datasets, there is still a non-negligible number of datasets for which the one-shot solution produced by each particular system would provide sub-par performance. In this paper, we present Amazon SageMaker Autopilot: a fully managed system providing an automated ML solution that can be modified when needed. Given a tabular dataset and the target column name, Autopilot identifies the problem type, analyzes the data and produces a diverse set of complete ML pipelines including feature preprocessing and ML algorithms, which are tuned to generate a leaderboard of candidate models. In the scenario where the performance is not satisfactory, a data scientist is able to view and edit the proposed ML pipelines in order to infuse their expertise and business knowledge without having to revert to a fully manual solution. This paper describes the different components of Autopilot, emphasizing the infrastructure choices that allow scalability, high quality models, editable ML pipelines, consumption of artifacts of offline meta-learning, and a convenient integration with the entire SageMaker suite allowing these trained models to be used in a production setting.
MLJ: A Julia package for composable Machine Learning
Jul 23, 2020
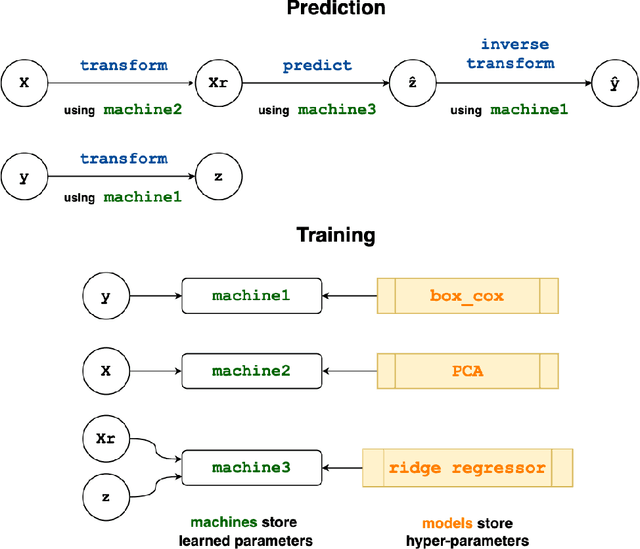
Abstract:MLJ (Machine Learing in Julia) is an open source software package providing a common interface for interacting with machine learning models written in Julia and other languages. It provides tools and meta-algorithms for selecting, tuning, evaluating, composing and comparing those models, with a focus on flexible model composition. In this design overview we detail chief novelties of the framework, together with the clear benefits of Julia over the dominant multi-language alternatives.
Distributed Bayesian Learning with Stochastic Natural-gradient Expectation Propagation and the Posterior Server
Sep 07, 2017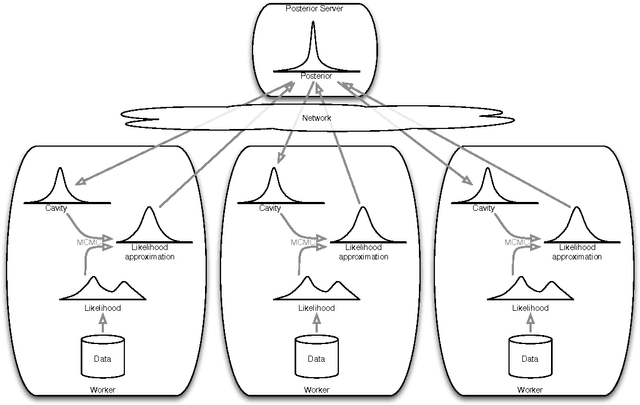
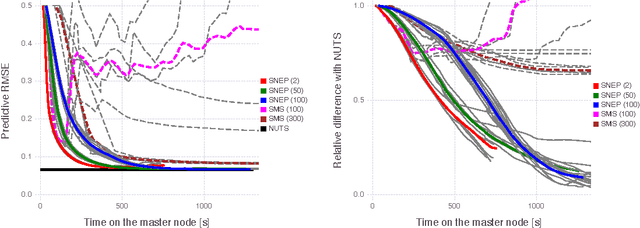

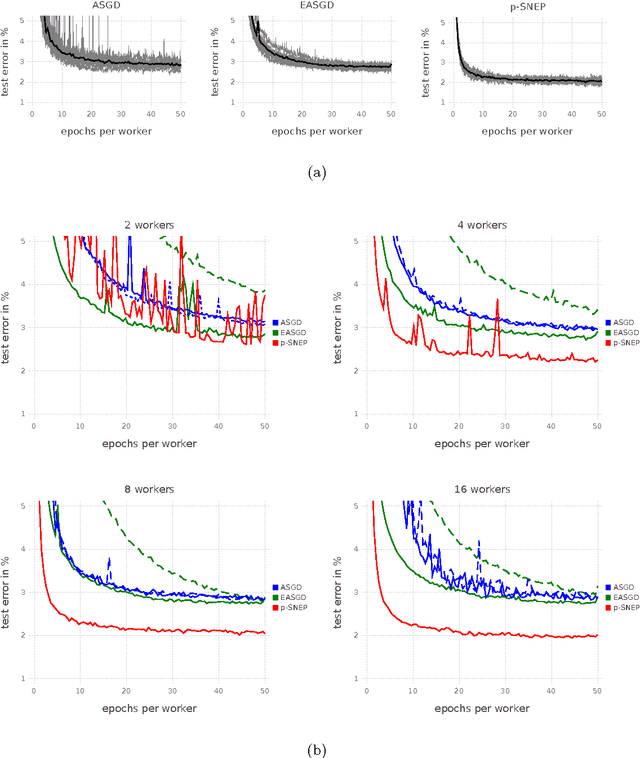
Abstract:This paper makes two contributions to Bayesian machine learning algorithms. Firstly, we propose stochastic natural gradient expectation propagation (SNEP), a novel alternative to expectation propagation (EP), a popular variational inference algorithm. SNEP is a black box variational algorithm, in that it does not require any simplifying assumptions on the distribution of interest, beyond the existence of some Monte Carlo sampler for estimating the moments of the EP tilted distributions. Further, as opposed to EP which has no guarantee of convergence, SNEP can be shown to be convergent, even when using Monte Carlo moment estimates. Secondly, we propose a novel architecture for distributed Bayesian learning which we call the posterior server. The posterior server allows scalable and robust Bayesian learning in cases where a data set is stored in a distributed manner across a cluster, with each compute node containing a disjoint subset of data. An independent Monte Carlo sampler is run on each compute node, with direct access only to the local data subset, but which targets an approximation to the global posterior distribution given all data across the whole cluster. This is achieved by using a distributed asynchronous implementation of SNEP to pass messages across the cluster. We demonstrate SNEP and the posterior server on distributed Bayesian learning of logistic regression and neural networks. Keywords: Distributed Learning, Large Scale Learning, Deep Learning, Bayesian Learn- ing, Variational Inference, Expectation Propagation, Stochastic Approximation, Natural Gradient, Markov chain Monte Carlo, Parameter Server, Posterior Server.
* 37 pages, 7 figures
Expectation Particle Belief Propagation
Jun 19, 2015


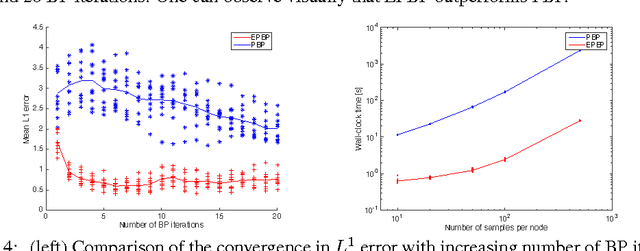
Abstract:We propose an original particle-based implementation of the Loopy Belief Propagation (LPB) algorithm for pairwise Markov Random Fields (MRF) on a continuous state space. The algorithm constructs adaptively efficient proposal distributions approximating the local beliefs at each note of the MRF. This is achieved by considering proposal distributions in the exponential family whose parameters are updated iterately in an Expectation Propagation (EP) framework. The proposed particle scheme provides consistent estimation of the LBP marginals as the number of particles increases. We demonstrate that it provides more accurate results than the Particle Belief Propagation (PBP) algorithm of Ihler and McAllester (2009) at a fraction of the computational cost and is additionally more robust empirically. The computational complexity of our algorithm at each iteration is quadratic in the number of particles. We also propose an accelerated implementation with sub-quadratic computational complexity which still provides consistent estimates of the loopy BP marginal distributions and performs almost as well as the original procedure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge