Iaroslav Shcherbatyi
Amazon SageMaker Autopilot: a white box AutoML solution at scale
Dec 16, 2020
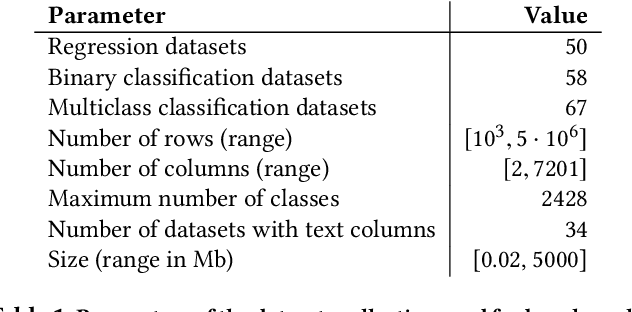
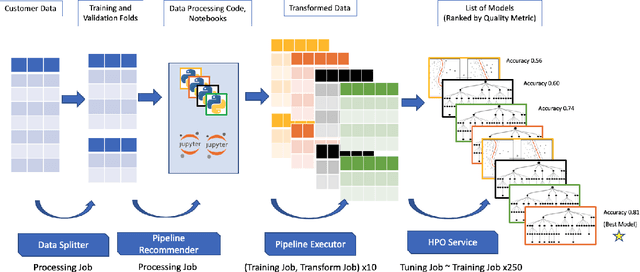
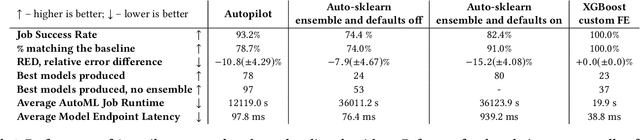
Abstract:AutoML systems provide a black-box solution to machine learning problems by selecting the right way of processing features, choosing an algorithm and tuning the hyperparameters of the entire pipeline. Although these systems perform well on many datasets, there is still a non-negligible number of datasets for which the one-shot solution produced by each particular system would provide sub-par performance. In this paper, we present Amazon SageMaker Autopilot: a fully managed system providing an automated ML solution that can be modified when needed. Given a tabular dataset and the target column name, Autopilot identifies the problem type, analyzes the data and produces a diverse set of complete ML pipelines including feature preprocessing and ML algorithms, which are tuned to generate a leaderboard of candidate models. In the scenario where the performance is not satisfactory, a data scientist is able to view and edit the proposed ML pipelines in order to infuse their expertise and business knowledge without having to revert to a fully manual solution. This paper describes the different components of Autopilot, emphasizing the infrastructure choices that allow scalability, high quality models, editable ML pipelines, consumption of artifacts of offline meta-learning, and a convenient integration with the entire SageMaker suite allowing these trained models to be used in a production setting.
Amazon SageMaker Automatic Model Tuning: Scalable Black-box Optimization
Dec 15, 2020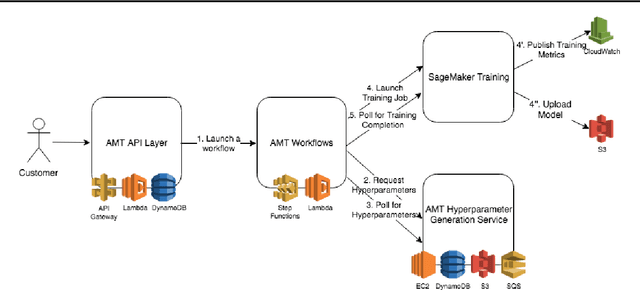
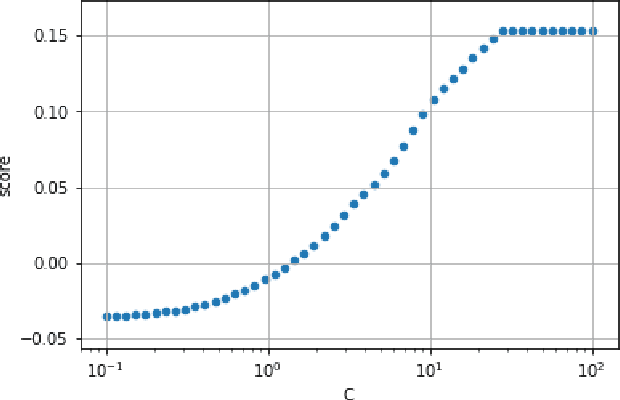
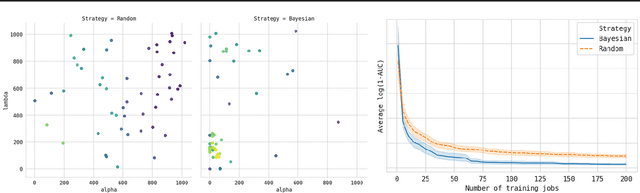
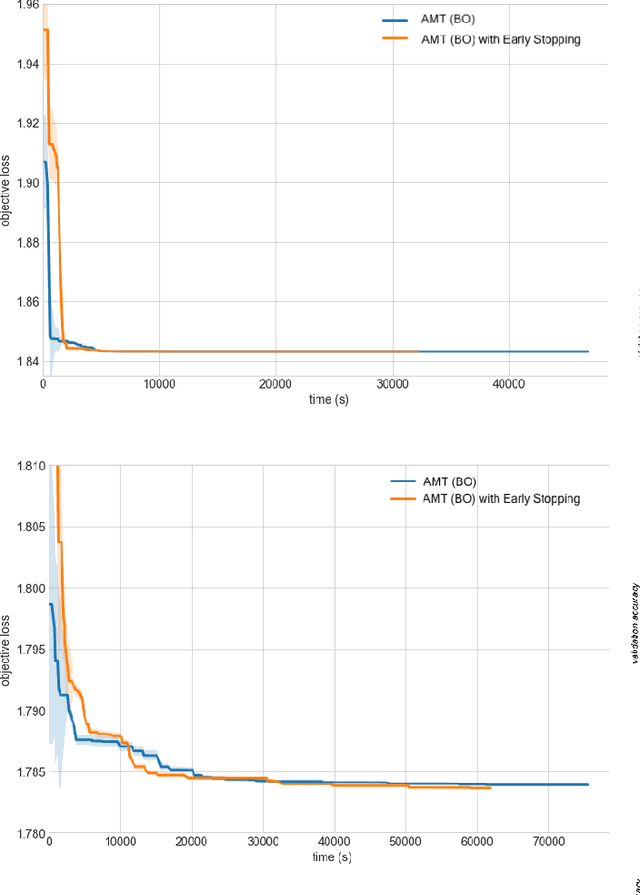
Abstract:Tuning complex machine learning systems is challenging. Machine learning models typically expose a set of hyperparameters, be it regularization, architecture, or optimization parameters, whose careful tuning is critical to achieve good performance. To democratize access to such systems, it is essential to automate this tuning process. This paper presents Amazon SageMaker Automatic Model Tuning (AMT), a fully managed system for black-box optimization at scale. AMT finds the best version of a machine learning model by repeatedly training it with different hyperparameter configurations. It leverages either random search or Bayesian optimization to choose the hyperparameter values resulting in the best-performing model, as measured by the metric chosen by the user. AMT can be used with built-in algorithms, custom algorithms, and Amazon SageMaker pre-built containers for machine learning frameworks. We discuss the core functionality, system architecture and our design principles. We also describe some more advanced features provided by AMT, such as automated early stopping and warm-starting, demonstrating their benefits in experiments.
Constrained Bayesian Optimization with Max-Value Entropy Search
Oct 15, 2019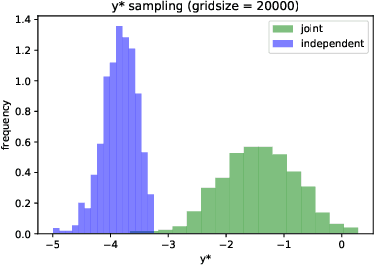
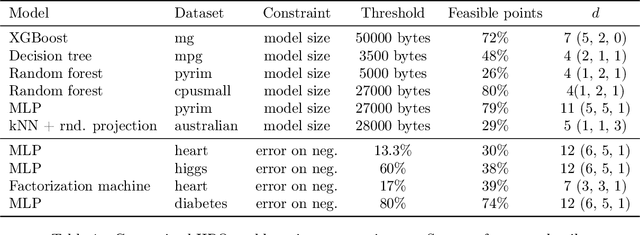
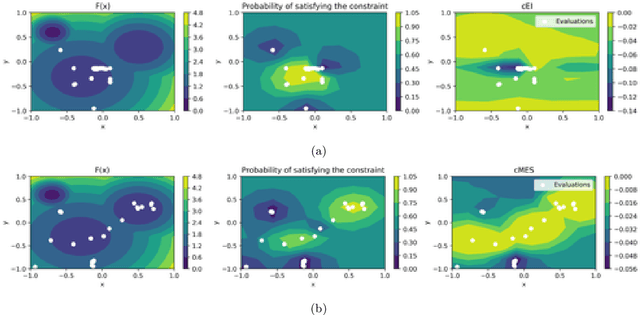
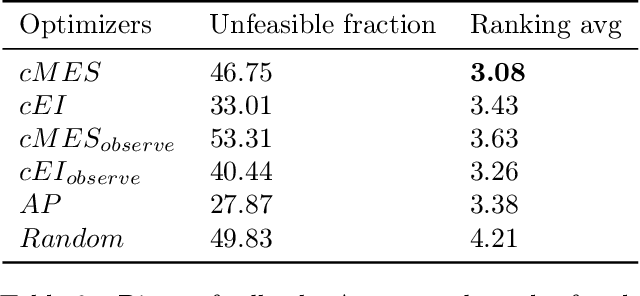
Abstract:Bayesian optimization (BO) is a model-based approach to sequentially optimize expensive black-box functions, such as the validation error of a deep neural network with respect to its hyperparameters. In many real-world scenarios, the optimization is further subject to a priori unknown constraints. For example, training a deep network configuration may fail with an out-of-memory error when the model is too large. In this work, we focus on a general formulation of Gaussian process-based BO with continuous or binary constraints. We propose constrained Max-value Entropy Search (cMES), a novel information theoretic-based acquisition function implementing this formulation. We also revisit the validity of the factorized approximation adopted for rapid computation of the MES acquisition function, showing empirically that this leads to inaccurate results. On an extensive set of real-world constrained hyperparameter optimization problems we show that cMES compares favourably to prior work, while being simpler to implement and faster than other constrained extensions of Entropy Search.
Convexification of Learning from Constraints
Feb 22, 2016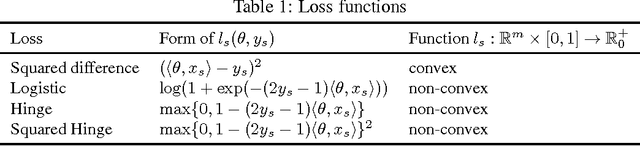
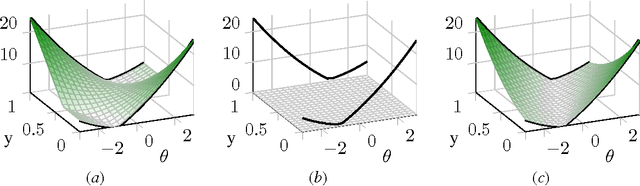
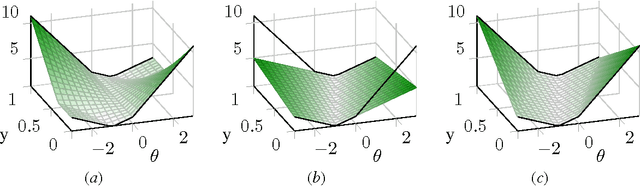
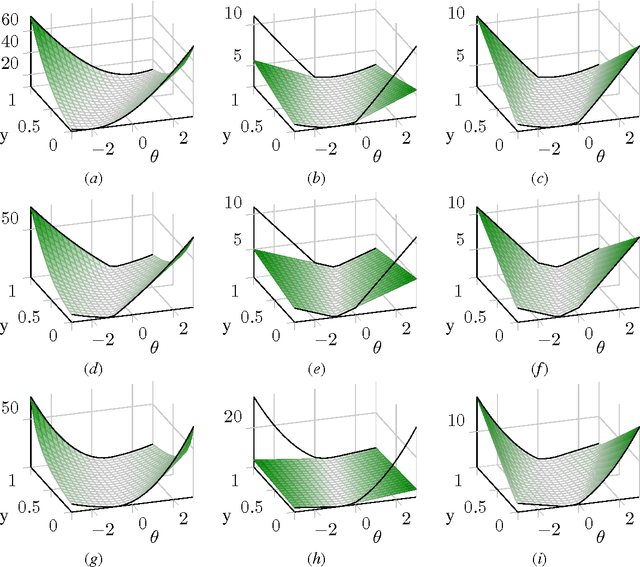
Abstract:Regularized empirical risk minimization with constrained labels (in contrast to fixed labels) is a remarkably general abstraction of learning. For common loss and regularization functions, this optimization problem assumes the form of a mixed integer program (MIP) whose objective function is non-convex. In this form, the problem is resistant to standard optimization techniques. We construct MIPs with the same solutions whose objective functions are convex. Specifically, we characterize the tightest convex extension of the objective function, given by the Legendre-Fenchel biconjugate. Computing values of this tightest convex extension is NP-hard. However, by applying our characterization to every function in an additive decomposition of the objective function, we obtain a class of looser convex extensions that can be computed efficiently. For some decompositions, common loss and regularization functions, we derive a closed form.
GazeDPM: Early Integration of Gaze Information in Deformable Part Models
May 21, 2015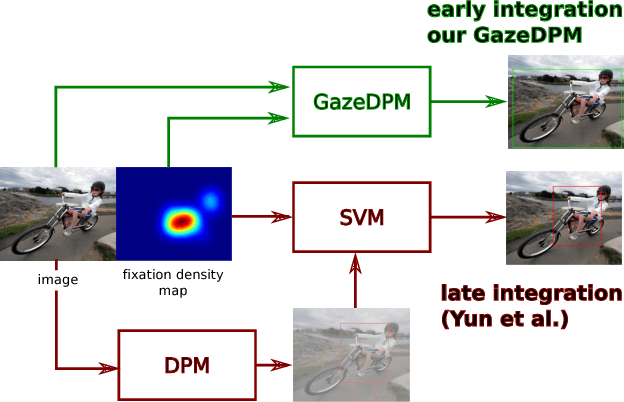
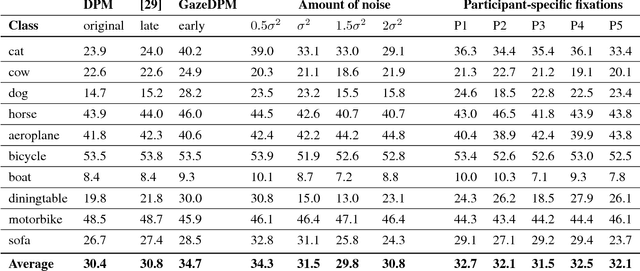

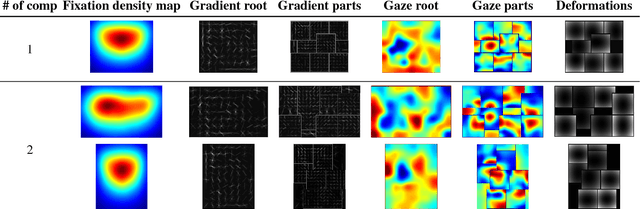
Abstract:An increasing number of works explore collaborative human-computer systems in which human gaze is used to enhance computer vision systems. For object detection these efforts were so far restricted to late integration approaches that have inherent limitations, such as increased precision without increase in recall. We propose an early integration approach in a deformable part model, which constitutes a joint formulation over gaze and visual data. We show that our GazeDPM method improves over the state-of-the-art DPM baseline by 4% and a recent method for gaze-supported object detection by 3% on the public POET dataset. Our approach additionally provides introspection of the learnt models, can reveal salient image structures, and allows us to investigate the interplay between gaze attracting and repelling areas, the importance of view-specific models, as well as viewers' personal biases in gaze patterns. We finally study important practical aspects of our approach, such as the impact of using saliency maps instead of real fixations, the impact of the number of fixations, as well as robustness to gaze estimation error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge